高校开办系列论坛的博弈分析
赵佳昕
摘要:纳什均衡是博弈论里面很常见到的一种均衡。文章就高校举办的系列论坛为例。对论坛的举办方研究生会和参与者学生之间进行博弈分析,找出纳什均衡。
关键词:博弈;均衡;模型
中图分类号:O225~49
文献标识码:A
文章编号:1006-8937(2009)16-0080-02
1框架分析
在各大高校中,我们对一些论坛的开办已经司空见惯,习以为常,但是并不是所有的论坛都带着“高水平”的帽子。因此,我们对论坛的主办方与学生之间的博弈进行一下深入思考,尽可能地找出战略选择的纳什均衡。
此模型是建立在两个群体参与人之上的,一方是研究生会(模型中用Y表示),另一方是学生集体(模型中用S表示);研会举办论坛的很大一部分目的是为了从赞助商那里得到赞助,当然,其为了提高学生集体的素质水平也是目的之一,不管目的如何,研会始终有两个战略选择:{举办一场精彩的论坛,应付了事},同时,学生集体有理由去选择听还是不昕,其中,用G和B来分别代表精彩的论坛和一般论坛,用L和U分别代表听和不听,这里有一个关键假设,那就是,学生成为一个集体,集体内的信息是完全的,并且具有羊群效应。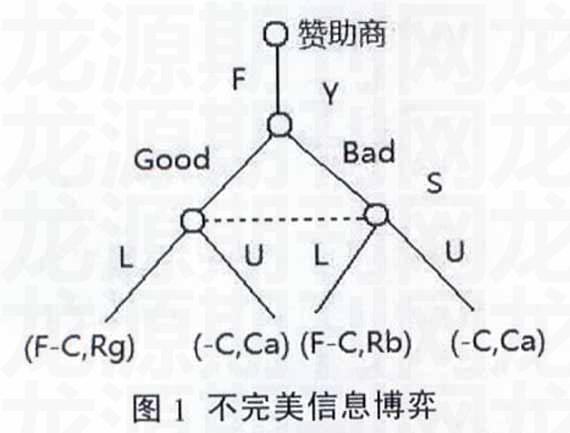
如果学生集体参加论坛,那么研会就可以顺利拿到赞助费F,否则,会被扣钱,另外举办论坛成本固定为c;对于学生而言,其时间是有成本的,如果不去参加论坛,可以把时间用来看书、唱歌等,同时也就失去了从论坛中获得收益的机会,而如果这是一场精彩的论坛,其收益会抵消时间的机会成本,并有所剩余,否则,学生是有损失的。学生时间的机会成本表示为Ca,精彩论坛带来的收益(即满足程度)为Rg,一般的论坛带来的收益(满足程度)为Rb,很明显的一个关系式是Rg>Ca>Bb。
2模型分析
首先考虑第一种情况,这是一个不完美信息博弈,此时的博弈树如图1所示。
从图1可以看出,赞助商首先将赞助费F支付给研会(Y),然后研会选择论坛质量的好坏,接下来学生选择是听还是不听,进而给出双方参与人的支付情况:①研会举办的论坛精彩,并且学生集体参加,此时研会和学生集体对应支付为(F-C,Rg)。②研会举办的论坛糟糕,但是学生集体参加,此时研会和学生集体对应支付为(F-C,Rb)。③研会举办的论坛精彩,但是学生集体不参加,此时研会和学生集体对应支付为(-C,Ca)。④研会举办的论坛糟糕,并且学生集体不参加,此时研会和学生集体对应支付为(-C,Ca),注意图中虚线,其表示信息集只有一个,该信息集包含了两个决策结,这意味着学生群体并不了解论坛的性质。
此博弈的NE可以通过转换成静态博弈的形式来求得,如表1所示。
从上表看出,当研会选择GOOD时,学生的最优战略选择为LISTEN,而当选择Bad时,学生最优选择为UN-LISTEN;同样,当学生选择LISTEN时,研会最优选择为GOOD,学生选择UNLISTEN时,研会最优选择是BAD。这样,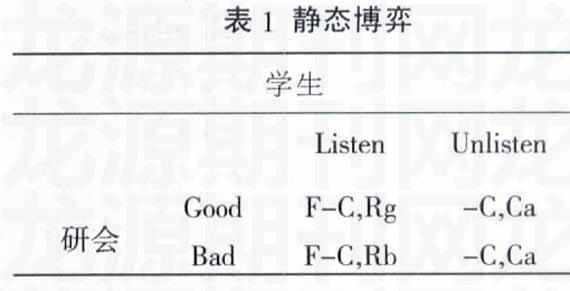 从次静态博弈来看,有两个NE,即(G,L)和(B,U)。但是在博弈树中可以看到,研会是先行者,由于其在做出选择前肯定会考虑到未来的收益,并且其拉赞助是为了获取收益,而不是亏本,所以(B,U)是不可置信的,也就是说可置信的NE为(G,L)。
从次静态博弈来看,有两个NE,即(G,L)和(B,U)。但是在博弈树中可以看到,研会是先行者,由于其在做出选择前肯定会考虑到未来的收益,并且其拉赞助是为了获取收益,而不是亏本,所以(B,U)是不可置信的,也就是说可置信的NE为(G,L)。
举办一场精彩的论坛,并且座无虚席是我们经常可以看到,下面我们看看另一种在校园中经常发生的现象:即不知名的论坛依旧可以座无虚席,这主要是通过改变支付来改变NE,这里要改变一个假设,即研会举办精彩论坛的成本为C1,大于举办糟糕论坛的成本C2。
此博弈的博弈树如图2所示,其中除了成本改变为C1和C2外,还改变了学生在听取糟糕论坛时的收益,这种改变可以采取在论坛进行或者结束时抽奖、派发礼物等形式,目的就是提高学生的预期收益,并且要大于时间的机会成本,因此Rp>Ca,但是即使是这样,C2依然要小于C1。
如此,根据逆向归纳法,在左边的子博弈树中,学生肯定选择L,在右边的子博弈树中,学生肯定也选择L,向上推进,当研会选择时,肯定会选择成本较低但仍可以拿到赞助费的Bad,此时NE因支付的改变发生了变化(一种承诺行动),NE为(B,L)。
这一模型从一定程度上解释了为什么有些论坛其貌不扬,但却依然火爆的原因:即学生参加BAD论坛所获收益能超过其时间的机会成本,并且主办单位办BAD论坛的支付大于办GOOD论坛的支付。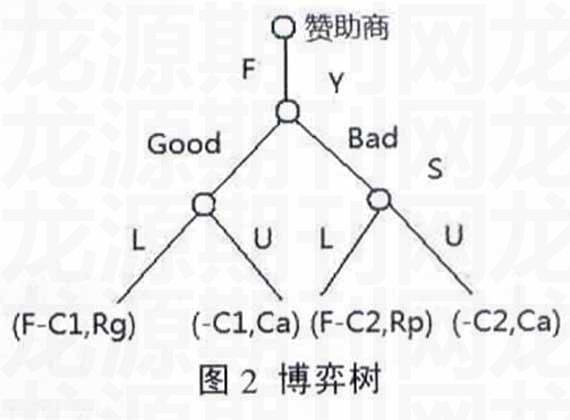
考虑另一种理想的情况:赞助商在支付完赞助费后没有任何契约限制,即使无人参加也不会扣除费用,这种情况比较少见,一般建立在双方比较信任的基础上,那么考虑单期博弈,其博弈树应如图3所示。
如图3所示,成本依然分为C1和C2两种情况,只是研会的收益发生了改变,即无论是否有人参加,都能拿到F这部分的赞助费用,这也将改变NE。根据逆向归纳法,在子博弈1中,学生集体会选择L,在子博弈2中,学生集体会选择u,当研会选择时,由于选择GOOD带来的收益F-C1小于选择BAD的收益F-C2,因此NE为(B,U)。这种情况在一些大公司与大型教育机构之间合作时时常会出现,因为大型教育机构会考虑到自己的声誉问题,所以将风险降低了,下面的分析中会看到这点。
考虑最后一种情况,当把研会这个集体扩展为学校时,NE又会发生变化,由于学校与研会相比,更需要考虑的是学校的声誉,因此学校有很大的动力考虑其学术水平(包括开办论坛)以及学生的素质提高,进而在模型分析中加入一个重要的因素:学校收益中一部分来自学生集体的满意程度(以其收益度量)。那么这种情况的博弈树如图4所示。
如图所示,其中a代表学校的收益与学生的收益之间的弹性比,赞助商的费用依然是一次性支付并且无返还,根据逆向归纳法,学生在两个子博弈中分别选择L和U,在学校的选择中则要取决于F-C1+aRg与F-C2的对比,只 以上一共分析了高校研会(最后扩大到学校)举办论坛的四种情况,主要是为了说明承诺行动的实施会改变NE,因此,为了达到某种目的,可以考虑改变支付、改变偏好以及减少行动空间等手段。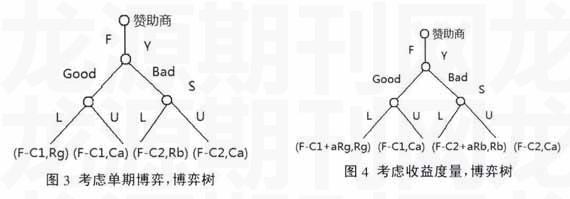 要C1-aRg
要C1-aRg

