单中心视角下杭州都市经济圈内经济增长关联性的实证研究

林 明

摘要:区域经济发展的相关理论表明,都市经济圈的形成与发展需要一个强有力的中心。文章对杭州都市经济圈的杭州与嘉兴、湖州、绍兴3地之间的经济增长(率)的相互关联性进行了探讨,通过格兰杰因果检验表明,杭州经济增长率对嘉兴、湖州地区的经济增长率的影响不是很显著,而对绍兴的经济增长率是显著的。因此,目前杭州都市经济圈的发展还处于低级阶段,并不存在明显增长极的中心。

关键词:格兰杰因果检验;杭州;都市圈;强心

一、问题的提出

杭州都市经济圈的范围包括杭州、嘉兴、湖州、绍兴4市全境的区域,总面积34585平方公里。有关杭州都市经济圈研究方面,李王鸣等人(1998)分析了杭州都市区经济集聚与扩散机制,认为经济技术革新与产业结构升级是根本动力,区位和交通条件是诱因,政府规划是指导,政策是催化剂。徐长乐(2007)提出,政府在推动杭州都市圈构建中要有所作为,要积极发挥统筹规划、资源整合的作用。王东祥(2008)认为目前杭州都市经济圈的规划首要做的是确定核心的范围,确定核心与周边地区的经济联系程度及其影响范围。在现有的规划中,人们都假设杭州已经是都市经济圈的中心,杭州城区是都市经济圈的核心,但是,杭州经济增长是否已经形成对湖州、嘉兴、绍兴3个城市的经济增长产生显著的影响还缺乏定量分析。所以,本文试图通过区域经济增长的空间依赖性定量分析都市经济圈内的经济增长(率)联系及差异问题,以验证杭州都市经济圈内的中心与外围之间是否存在长期稳定的增长关系与因果关系,以及杭州都市经济圈的中心与外围经济增长之间的空间依赖性。

二、都市圈的相关理论与假设

都市圈是区域产业空间重组的产物,是中心城市对社会经济要素聚集与扩散到一定阶段的必然结果。在区域经济经典理论方面,佩鲁的增长极理论、布代维尔等人的区域发展极、缪尔达尔的累积因果关系理论、赫希曼的中心-外围理论以及弗里德曼的空间极化理论,都强调了区域经济增长的不平衡规律,认为区域经济发展中存在着经济核心或增长极,其与外围之间的联系主要是通过资源要素的积聚与扩散来完成。中心城市核心圈层的能级是影响整个都市圈能级和大小的重要因素,在都市圈的形成过程中,各种要素在中心城市的聚集与扩散是最基本的前提。随着社会经济的发展与产业结构的调整,一些产业向城市中心聚集以获取规模聚集效益,并推动原有产业向外扩散;当聚集到一定规模或产业结构升级后,部分产业再一次向外扩散,从而形成聚集-扩散-聚集-扩散的产业空间重组循环,使城市由中心向郊区呈现核心城市区、近郊区、远郊区的圈层式结构。中心城市与外围城市之间通过要素的不断聚集和扩散促进了大都市圈的不断发展。一个强大的中心城市对都市圈具有十分重大的意义,一方面,中心城市的规模和能量决定了它辐射的远近,从而决定了都市经济圈范围的大小,另一方面,都市圈的中心与次中心之间的经济增长的关联度,决定了都市经济圈的发展水平。杭州都市经济圈属于区域经济的范畴,它是以杭州为中心,嘉兴、湖州和绍兴为次中心的都市经济圈发展模式,从区域经济的相关理论来讲,以杭州为增长极必然会形成杭州对其他处于次中心城市的要素的积聚——扩散作用。作为都市经济圈次中心的湖州、嘉兴、绍兴3个城市的经济增长(经济增长率)将受到杭州经济增长(经济增长率)的影响,而如果市场是高度开放且紧密联系的话,杭州的经济增长(经济增长率)将成为影响各个次中心经济增长(经济增长率)的因素,因此我们假设:

H1:杭州的经济增长(经济增长率)是影响嘉兴的经济增长(经济增长率)的因素。

H2:杭州的经济增长(经济增长率)是影响湖州的经济增长(经济增长率)的因素。

H3:杭州的经济增长(经济增长率)是影响绍兴的经济增长(经济增长率)的因素。

三、杭州都市经济圈经济增长关系的实证分析

(一)数据来源及分析工具

本文所用1978-2008年的数据来自于《杭州统计年鉴2009》、《嘉兴统计年鉴2009》、《湖州统计年鉴2009》、《绍兴统计年鉴2009》和《上海统计年鉴2009》公布的以1978年为基期的各个地方的国民生产总值的指数,总共有31组数据。其中杭州的GDP指数用HANGGDP表示、嘉兴的GDP指数用JIAGDP表示、湖州的GDP指数用HUGDP表示、绍兴的GDP指数用SHAOGDP表示、上海的GDP用SHANGGDP表示。为了消除数据中存在的异方差性,再分别对每个变量取对数,就是:LY1=log(HANGGDP),LY2=log(JIA GDP),LY3=log(HUGDP),LY4=log(SHAOGDP)。其相应的一阶差分序列分别为:△LY1、△LY2、△LY3和△LY4。这里一阶差分的经济含义代表着地区的经济增长率。本研究使用的软件是Eviews(5.1)软件。

(二)时间序列的平稳性及协整检验

为了研究相关关系,一般的做法是根据现有的样本资料建立比较合适的回归方程。但是在进行传统的回归分析时,要求所用的时间序列必须是平稳的,否则会产生所谓的“伪回归”问题。所以,我们首先本文采用PP检验,对LY1、LY2、LY3、LY4进行平稳性检验。计算结果,序列LY1、LY2、LY3、LY4的PP统计量值分别为-2.01242、-2.23143、-2.41032和-1.36179,对应的99%置信水平的临界值是-4.2967,均不能拒绝序列存在单位根的零假设,因而它们都是非平稳的。对LY1、LY2、LY3、LY4的一阶差分变量△LY1、△LY2、△LY3和△LY4进行平稳性检验。结果是:△LY1、△LY2、△LY3、△LY4的PP统计量值分别为-2.58160、-3.63322、-3.13312和-2.36497,对应的99%置信水平的临界值是-4.309824,均不能拒绝序列存在单位根的零假设,因而它们都是非平稳的。由于一阶差分变量△LY1、△LY2、△LY3和△LY4是非平稳的,因此,LY1、LY2、LY3、LY4之间不具有协整关系。我们进一步对对LY1、LY2、LY3、LY4的二阶差分变量△2LY1、△2LY2、△2LY3和△2LY4进行平稳性检验。结果是:△2LY1、△2LY2、△2LY3、△2LY4的PP统计量值分别为-3.78589、-6.59064、-6.86968和-4.40410,对应的99%置信水平的临界值是-3.58062,全部拒绝序列存在单位根的零假设,因而它们都是平稳的,因此序列LY1、LY2、LY3、LY4都具有二阶单整。

(三)格兰杰因果检验

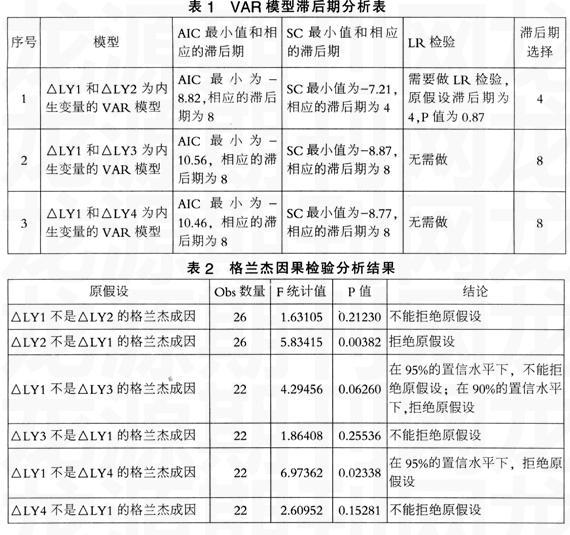
格兰杰(Granger)因果检验在考察序列A是否是序列B产生的原因时,先估计当前的B值被其自身滞后期取值所能解释的程度,然后验证通过引入序列A的滞后值是否可以提高B的被解释程度,如果是,则称序列A是B的格兰杰成因(Granger Cause),此时A的滞后期系数具有统计显著性。变量是否平稳会影响Granger因果检验。在变量均非平稳且不协整的情况下,可以在差分的基础上建立VAR模型,此时只可以检验短期的因果关系(陈雄兵、张宗成,2008)。格兰杰(Granger)因果检验的具体结论对滞后阶很敏感(Gujarati,1995)。因此需要在向量自回归模型确定滞后期的基础上进行格兰杰成因果检验。向量自回归模型的滞后期确定,一般根据AIC和SC的信息量取值最小的准则,如果AIC和SC取最小值时最大滞后期不一样的话,应该考虑LR检验(易丹辉,2002)。我们对于模型滞后期的选择参见表1。对于模型1来说,AIC滞后期为8时最小,为-8.82;SC滞后期为4时最小,为-7.21,因此,需要进行LR检验,检验的原假设是模型最大的滞后期为4,检验的统计量LR有渐进的X2分布,自由度为24,可以得到P值为0.87,因此不能拒绝原假设,即采取滞后期为4的情况。对于模型2和模型3来说,AIC最小时的滞后期与SC最小时的滞后期一样。在确定每个模型的滞后期后,我们对序列的一阶差分进行格兰杰(Granger)因果检验,检验结果见表2。

以上对Granger因果检验的结果显示:第一,杭州的经济增长率不是嘉兴经济增长率的格兰杰成因,因此假设H1不成立,但是嘉兴的经济增长率是杭州的经济增长率的格兰杰成因。第二,至少在90%的置信水平下,杭州的经济增长率是湖州经济增长率的格兰杰成因,但是在95%的置信水平下,杭州的经济增长率不是湖州经济增长率的格兰杰成因,因此假设H2不完全成立。另外,湖州的经济增长率不是杭州经济增长率的格兰杰成因。第三,在95%的置信水平下,杭州的经济增长率是绍兴经济增长率的格兰杰成因,因此假设H3成立,但是,绍兴的经济增长率不是杭州经济增长率的格兰杰成因。

四、结论与展望

从整体情况来说,我们可以得出:杭州都市经济圈内中心城市(杭州)的经济增长率与另外3个次中心城市的经济增长率之间经济关联性弱,杭州中心的作用还不很明显,仍处于弱中心的地位。尽管本文对杭州都市经济圈的中心与外围地区之间的经济增长的空间依赖关系进行了分析,但并没有解决弱中心的问题,将来可以进一步从以下3个方面做深入的研究:第一,需要增强杭州都市经济圈的区域创新能力,促进杭州的产业结构升级。第二,如何进行跨区域的产业对接、合作、转移,是否可以在杭州城区与嘉兴、湖州、绍兴城区之间建立产业过渡集聚区。在杭州与德清、安吉、海宁、桐乡、绍兴、诸暨6个县(市)之间的边界共同建立边界经济合作区。第三,如何以行政管理体制创新促进产业合理的布局。目前,杭州都市经济圈设立了市长联席会议,并组建规划、交通、产业、环保、旅游、宣传6个专业委员会,这些制度上的创新有利于促进区域合作与发展,但是各个区域都有自身的经济利益,产业上转移和重新布局将会影响各自的经济利益,利益上的协调和处理会带来较大的成本和困难。

参考文献:

1、李王鸣,陈秋晓,戴企成.杭州都市区经济集聚与扩敞机制研究[J].经济地理,1998(1).

2、袁家冬,周筠,黄伟.我国都市圈理论研究与规划实践中的若干误区[J].地理研究,2006(1).

3、Gujarati,D..Basic Econometrics[M].McGraw-Hill,1995.

4、易丹辉.数据分析与EVIEWS应用[M].中国统计出版社,2002.

5、陈雄兵,张宗成.再议Granger因果检验[J].数量经济技术经济研究,2008(1).

*本文系浙江省教育厅科研项目《单中心视角下杭州都市经济圈经济增长关联性的实证研究》(项目编号:Y200803846)的阶段性成果。

(作者单位:浙江工商职业技术学院。作者为该单位工商企业管理专业主任、管理学博士)