有趣的火柴棒问题

王宏愿

一根普通火柴棒的长度大约为4 cm，但是用数根这样的火柴棒可以摆成许多奇妙的数学图形，而且图形中还蕴涵着许多数学道理呢．

一、探索规律

例1如图1是小明用火柴棒搭的1条、2条、3条“金鱼”，…，则搭n条“金鱼”需要火柴棒_______根．

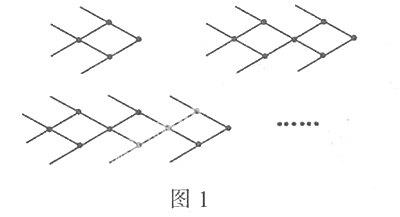
分析：1条“金鱼”需要火柴棒的根数为8＝6×1＋2；2条“金鱼”需要火柴棒的根数为14＝6×2＋2；3条“金鱼”需要火柴棒的根数为20＝6×3＋2；……

所以，搭n条“金鱼”需要火柴棒的根数为6n+2．

例2用火柴棒按如图2所示的方式摆图形，按照这样的规律继续摆下去，第4个图形需要___________根火柴棒，第n个图形需要_________根火柴棒（用含n的代数式表示）．

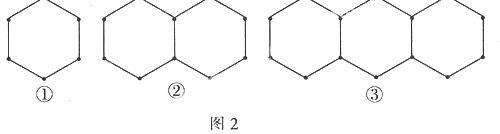
分析：第1个图中火柴棒的根数为6＝5×1＋1；第2个图中火柴棒的根数为11＝5×2＋1；第3个图中火柴棒的根数为16＝5×3＋1；……

所以，第n个图形中火柴棒的根数为5n+1，所以第4个图形需要火柴根的根数为4×5+1=21.

二、确定个数

例3用12根火柴棒（等长）拼成一个三角形，火柴棒不允许剩余、重叠和折断，则能摆出不同形状的三角形（注：三角形的任意两边之和大于第三边，任意两边之差小于第三边）的个数是（）．

Ａ.1 Ｂ.2 Ｃ.3 Ｄ.4

分析：设摆出的三角形的三边长为a，b，c，且a≤b≤c，则可得4≤c≤6．

当c=4时，b=4，a=4．

当c=5时，b=4，a=3；或b=5，a=2．

当c=6时，易知三角形不存在.

综上所述，满足条件的三角形有3个，故选Ｃ．

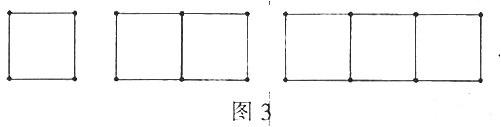
请读者解决下面这个“用火柴棒搭正方形”的问题.

问题：按图3所示的方法搭正方形，搭1个正方形需要4根火柴棒.

（1）搭2个正方形需要几根火柴棒？搭3个正方形需要几根火柴棒？

（2）搭10个正方形需要几根火柴棒？

（3）搭100个正方形呢？你是怎样得到的？

（4）如果用x表示搭正方形的个数，那么搭x个这样的正方形需要多少根火柴棒？

提示：前三个小问题解法略.第四个小问题的解法有：①第一个正方形用4根，以后每一个正方形都有3根，那么搭x个正方形需要［4+3（x-1）］根；②因为除第一个正方形外，其余正方形都只用3根，如果把第一个正方形所用的火柴棒也看成3根，x个正方形就需要（3x+1）根；③上面和下面一排各用了x根，竖直方向用了（x+1）根，于是搭x个正方形就需要［x+x+（x+1）］根；④把每个正方形都看成4根搭成，但除了第一个正方形需要4根，其余（x-1）个正方形中每个正方形均多用了1根，应减去，于是得到［4x-（x-1）］根.