运用遗传算法优化车间作业调度问题

摘要：在车间作业调度数学表达模型的基础上，研究了遗传算法对该问题的解决策略和过程。在算法流程的基础上，讨论了求解JSP问题遗传算法的具体设计，包括染色体编码设计、目标函数、遗传算子设计、选择策略设计等，最后给出了对不可行调度的处理方案。

关键词：车间作业调度问题；遗传算法；不可行调度

中图分类号：TP301文献标识码：A文章编号：1009-3044(2008)18-2pppp-0c

A Genetic Algorithm for Job Shop Scheduling Problem Optimization

HUANG Shao-rong

(Department of Information Management,Guangdong Justice Police Vocational College,Guangdong 510520,China)

Abstract:This paper gives out the mathematics model of JSP and the skeleton of,researches the strategies and processes of solving JSP by genetic algorithm,and discusses the design of GA in detail,then gives the mothed to solve the unfeasible scheduling solutions.

Key words:genetic algorithms;Job-shop Scheduling Problem;unfeasible scheduling solutions

1 引言

车间作业调度问题JSP（Job-shop Scheduling Problem）是一类求解困难的组合优化问题，实际是资源上的分配，求解目标是要找到一个将一组工件安排到设备上去，以使作业可为“最优”完成的方案。每个作业由一组任务组成，而每个任务必须由特定的设备处理，调度就是按先后顺序条件将所有任务安排到设备上的一种方案。通常，约束条件很多，使JSP成为一个难解的组合问题，是调度问题中最典型也是最困难的问题之一。

目前求解JSP问题的方法包括解析方法、穷举方法、分支定界法、动态规划法、拉格朗日松驰法和神经网络映射算法等。但由于问题本身难度很大，多数现有的优化算法只适用于规模较小的问题，另外，工业界依靠经验或计算机模拟得到的可行调度也不能保证最好的性能。

遗传算法作为一种有效的全局优化工具在JSP问题上的应用，是近年来才发展起来的研究方向，对复杂工业过程的建模、控制和优化领域的研究有重要的理论意义和工程价值。

2 JSP问题描述

设n个作业m台机器的车间作业调度问题（n/m JSP）满足下列约束条件：(1)一个作业由若干道工序组成；(2)每道工序必须在它前面的工序加工完毕后再加工；(3)每道工序必须在指定的机器上加工；(4)每道工序从加始到结束，不会被另外的工序中断。问题定义为：

(1)n个工件的集合{1,2,…,n}，m台机器的集合{1,2,…,m}；

(2)工序(i,j,k)表示作业i的第j道工序在机器k上执行，其中1≤i≤n，1≤k≤m，若工件i的工序数为pt，记p0=max(p1,p2,…,pn)，p=p1+p2+…+pn；

(3)矩阵W=(wij)n×p0为工序的耗时矩阵，wij表示执行工件i的第j道工序耗时，当j>pt时，wij=0；

(4)子集Work(a)={(i,j,k)|k=a} 1≤a≤m，表示共享机器a的工序集，记集合Work(a)的元素个数为La；

(5)一个调度S被定义为S=(S1,S2,…,Sm)T，其中Sa=(ga1,ga2,…,gaLa)是Work(a)中工序的一种排列(1≤a≤m)。即一个调度是由m台机器上加工工序的排列组成；

(6)T(S)表示在调度策略S下的一个性能指标，求解目标就是寻找一个满足约束的调度S，使T(S)最优。

3 解JSP遗传算法流程

遗传算法是一种基于自然选择和自然遗传机制的随机搜索算法，其求解JSP的具体流程如下：

Step1：问题的染色体设计，种群规模为Popsize的初始可行解生成。

Step2：定义调度问题的适应度函数(Fitness)，评价个体的适应度值。

Step3：按某种选择策略选择下一代种群。

Step4：对种群中的个体进行了遗传操作，生成新个体。

Step4a：按交叉概率Pm对种群中未匹配的个体对进行交叉操作，生成新个体。

Step4b：按变异概率Pc随机选择个体，进行变异操作生成新个体。

Step5：计算新个体的适应度值，父代个体和子代个体共同参与生存竞争。

Step6：判断算法是否达到终止条件，是则停止算法运行，最优个体为问题的最终解；否则转Step3。

以下将分别讨论求解JSP问题遗传算法的具体设计，主要包括染色体编码设计、目标函数、遗传算子设计、选择策略设计等。

4 算法分析

4.1 遗传算法染色体编码

鉴于JSP的组合特性以及工艺约束性，编码可归纳为直接编码和间接编码两种：①直接编码将各调度作为状态，通过状态演化达到寻优目的，主要包括基于操作的编码、基于工件的编码、基于工件对关系的编码、基于完成时间的编码、随机键编码等。②间接编码将一组工件的分配处理规则作为状态，算法优化的结果是一组最佳的分配规则序列，再由规则序列构造调度，主要包括基于优先权规则的编码、基于先后表的编码、基于析取图的编码和基于机器的编码等。

在所有的编码方式中，使用最多的是基于优先权规则的编码。在这种编码中，每个基因链由n条子链所构成，一条子链对应于一台机器。子链的长度为n即该机器上工件的个数，链中的每个基因位表示一个工序，用这种编码产生的染色体可以方便地实施各种遗传操作。

4.2 Job Shop问题的目标函数

遗传算法中使用适应度这个概念来度量群体中各个个体在优化计算中有可能达到、接近或有助于找到最优解的优良程度。一般来说，在运行的初期阶段，适应度差距比较大，有可能导致在选择过程中几个个体占有很高比例，从而使遗传算法产生早熟现象。而在运行的后期阶段，群体的个体适应度可能非常接近，大部分个体的竞争力和最佳个体相差无几，可能进入随机选择过程。由此，可采用线性尺度变换，从而能实现在运行的不同阶段，对个体的适宜度进行适当的调整，扩大或缩小，避免早熟现象的发生。具体操作如下。

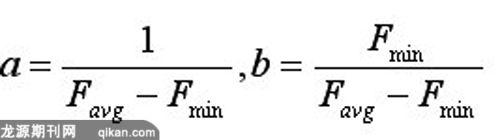
4.3 遗传算法染色体选择算子设计

采用比例选择方法，即回放式随机采样，每个个体被选中的概率与其适应度大小成正比。为了避免误差，可结合使用最优保存策略，即当前群体中最佳个体的适应度低于总的迄今为止的最好个体的适应度，用迄今为止的最好个体替换掉当前群体中的最差个体。

最优保存策略可视为选择操作的一部分，其实施可保证迄今为止所得到的最优个体不会被交叉、变异等遗传运算所破坏，是遗传算法收敛性的一个重要保证条件。

4.4 遗传算法染色体交叉算子设计

鉴于JSP的特殊性，遗传算法必须结合所采用的编码技术设计相应的交叉操作。置换编码是一种主要的交叉操作，表示JSP的置换码通常可分为两类，即单一文字串(pure literal string，PLS)和一般文字串(general literal string，GLS)，其中PLS由不同的文字排列而成，而GLS则允许所排列的文字重复出现。基于工件的编码和基于机器的编码采用PLS，而基于操作的编码、基于优先表的编码和基于先后规则的编码则采用GLS，其中基于优先表的编码所采用的GLS由若干个PLS构成。与PLS相关的交叉操作包括：部分映射交叉、次序交叉、基于位置的交叉、线性次序交叉、非ABEL群交叉和子调度互换交叉。非PLS下的交叉操作需要特殊设计，以保证染色体和对应解的可行性与合法性。

4.5 遗传算法染色体变异算子

变异操作的目的是通过随机改变染色体的某些基因来引入新个体，增加种群多样性，并在一定程度上进行局部搜索。常用针对置换编码的变异操作包括：(1)互换，即随机交换若干不同位置上的不同基因。(2)逆序，即将某两个随机位置间的基因串逆序。(3)插入，即将某一位置上的基因（或某一段位置上的基因串）插入到另一位置之前或之后。

4.6 交叉概率Pc和变异概率Pm

在经典遗传算法中，交叉和变异操作采用固定概率，不能反映种群的进化过程。自适应交叉和变异概率根据种群的进化状态来确定，使算法具有更好的收敛速度，其选取方法为：

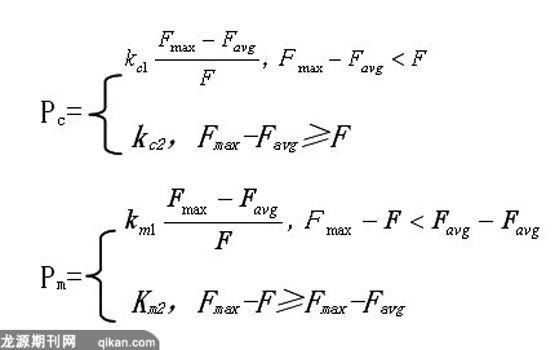
其中，Pc为交叉概率，Pm为变异概率，Fmax为种群个体中的最大适应度，Favg为种群个体的平均适应度，fc是参加交换的两个串中较大的适应度，fm是变异串的适应度，kc1、kc2、km1、km2为[0,1]之间的常数。Pc/Pm的自适应调整与算法的收敛程度成反比，能有效防止算法收敛于局部最小，同时，个体的适应度愈大，相应的Pc/Pm愈小，使好的进化结果得以保存。

5 不可行调度的处理

产生原因：(1)随机生成的原始种群中，由于没有检测措施，含有违反工序约束的调度和死锁调度。(2)在进化过程中，染色体的交叉和变异操作可能产生违反工序约束的调度和死锁调度。

解决方法：(1)生成全部由可行调度组成的原始种群。(2)在选择、交叉和变异过程中尽量避免产生违反工序约束的调度和死锁调度，如果产生了则要采取有效的响应修补措施。

检测和处理：(1)违反工序约束的调度的检测：判断各子染色体上的工序有没有按工序约束排列。处理：引入修正操作，在执行交叉和变异操作时，每产生一个新的个体，对该个体实施修正操作。(2)死锁调度的检测：模拟其调度过程，若在某一时刻，所有尚未完工的机器的状态都为空闲且这些机器上的首个未完工的状态都为等状态，则发生了死锁。解锁：交换这些染色体段上当前基因紧后的两个基因，再检测再交换，直到解锁为止。

6 小结

简要地分析了车间调度问题，利用遗传算法对JSP问题进行求解，并对算法做了详细分析，最后讨论了对不可行解的处理。

参考文献：

[1]王小平.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002:130-136.

[2]王凌.车间调度及其遗传算法[M].北京:清华大学出版社,2003:68-76.

[3]谢胜利.求解JSP的遗传算法中不可行调度的方案[J].计算机集成制造系统,2001,8(11).

[4]蔡良伟,张基宏.用自适应遗传算法求解一类组合调度优化问题[J].深圳大学学报:理工版,2004,21(3).

收稿日期：2008-04-03

黄少荣（1976-），女，广东饶平人，广东司法警官职业学院信息管理系计算机讲师，计算机应用硕士，主要研究方向：进化算法和人工智能。