大型集装箱船船舶尺度的一种确定方法

， ，

(大连海事大学 航海学院，辽宁 大连 116026)

近年来船舶的吨位越来越大，但关于大型船舶尺度的相关性研究却比较少，现有的数学模型已不能满足大型船舶的要求。因此以收集到的350多艘大型集装箱船实船基本数据为依据，根据船舶主尺度[1]及载重量等变化规律，对基本数据作统一处理，再运用曲线拟合方法建立数学模型。

1 回归模型的确定

使用F[2]统计量和决定系数r2[2]这2个重要的回归统计量来衡量模型的优良程度，并选择其中最优的一个作为回归模型。利用相关软件(如SPSS，Excel等)对船舶数据分别按照7种比较常见的回归模型进行处理，见文献[3]。并比较F和r2，F和r2值都比较大的模型就是要选择的模型。分析比较后，选择对数回归模型和指数回归模型。

2 数据处理

2.1 数据来源

所采用的船舶主尺度数据来源于Fairplay出版有限公司SeaBase船舶数据库，其中，295艘船吨位在4 500～6 500 t之间；62艘吨位大于6 500 t。

2.2 集装箱船尺度之间关系的数学模型

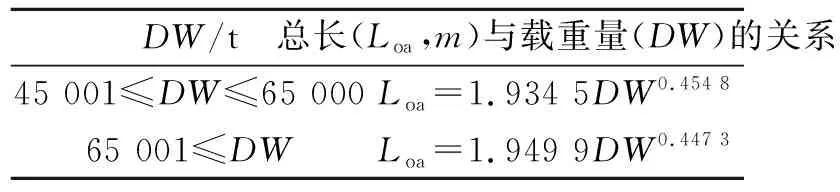
表1 总长与载重量之间关系的数学模型

表2 船宽与载重量之间关系的数学模型

表3 型深与载重量之间关系的数学模型

表4 吃水与载重量之间关系的数学模型

3 回归比较

选择2艘船进行实船与回归尺度对比，分别见表5、6。

表5 Ambassador Bridge(载重量45 739 t) m

表6 KateMaersk(载重量82 135 t) m

4 结束语

船舶主尺度在航道设计、港口规划尤其是泊位建设方面具有重要意义。船宽是航道设计必须考虑的主要因素，在泊位建设中船舶总长是必须考虑的因素之一。合理选择和确定主尺度是船舶总体设计中最基本最重要的工作之一，也是开展各项具体设计工作的基础。

[1] 蒋维清.船舶原理[M].大连：大连海事大学出版社，1997.

[2] 周纪芗.回归分析[M].上海：华东师范大学出版社，1993.

[3] 李树范.运输船舶可行性分析[M].大连： 大连理工大学出版社,1990.