基于分辨矩阵的论域划分方法
汪小燕
摘要:提出基于分辨矩阵的论域划分方法,该方法在建立相应的分辨矩阵后,能够快速计算不同的条件属性组合相对于决策属性的负域,从而推导出正域,且实现简单。
关键词:粗糙集分辨矩阵论域
粗糙集理论是Pawlak等学者在1982年提出的处理不确定,不精确和不完全数据的一种新的数学工具,主要用于知识的简化及知识依赖性的分析。属性约简是粗糙集理论中的重要研究内容之一,国内外学者提出了各种约简方法,这些约简方法中,很多需要考虑属性集对论域的划分,通过比较约简后的属性集和原属性集相对于决策属性的正域是否相等,来判断约简是否成立。传统的划分方法需要按照单个属性或多个属性分类,并执行集合求交取并集运算,为简化论域划分方法,提高论域划分速度,文中首先提出利用分辨矩阵计算负域的定理和推论,并结合相关理论提出一种基于分辨矩阵的论域划分方法。
1相关概念

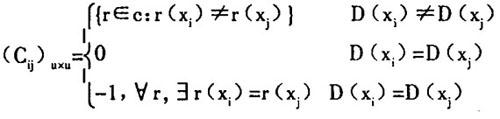
以上公式指出:当决策属性不同且条件属性也不完全相同时,元素值为互不相同的属性纽合;当决策属性相同时,元素值为0;当决策属性不同而条件属性完全相同时,元素值为-1,表明数据有误或提供条件属性不足,显然,分辨矩阵是一个按主对角线对称的矩阵,在考虑分辨矩阵的时候,只需考虑其上三角(或下三角)部分就可以了。
2基于分辨矩阵的论域划分
定理1:在信息决策系统分辨矩阵中,所有为-1的元素所对应的行列元素的并集构成条件属性相对于决策属性的负域,即NEGc(D)。
证明:在信息决策系统分辨矩阵中,若某一个元素为-1,则该元素所对应的行列元素的条件属性完全相同,决策属性不相同,这两个对象,根据现有的条件属性,无法确定归入哪一个决策类,而NEGc(D)中的对象是所有不能确定一定归入哪一个决策类的元素的集合。故在信息决策系统分辨矩阵中,所有为-1的元素所对应的行列元素的并集构成NEGc(D)。
由定理1可以得到:
推论1:设I=(U,C∪D)是一个信息决策系统,C是条件属性集,A∈C,D=(d)是决策属性集,则分辨矩阵中,某一条件属性组合A相对于决策属性的负域NEG

