从简单的情况想起
2007-07-23 16:26康健
小学生导刊(中年级) 2007年8期
康 健
例1.把3~9这6个数字分别填在下面等式的方框内,使每个等式成立。
分析与解:第二个等式只有乘法一种运算,比较简单。因此,先从第二个等式进行分析。
能使第二个等式成立的情况有两种:7×8=56或6×9=54。
如果第二个等式填7×8=56,剩下3、4、9这三个数,无论怎样填,都不能使第一个等式成立。
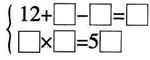
如果第二个等式填6×9=54,那么还剩下3、7、8,这3个数能使第一个等式成立,而且有两个答案。
答案为:
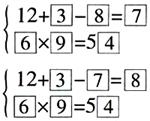
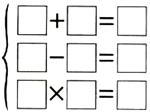
例2.把1~9这9个数字分别填在下面等式的方框内,使每个等式成立。
分析与解:根据题中的9个数字和3个等式分析,以满足第三个的情况为最少。在1~9中,能使第三个等式成立的情况只有两种:2×3=6或2×4=8。所以,我们可以把第三个等式作为解题的突破口。
如果第三个等式填2×4=8,剩下的1、3、5、6、7、9六个数,无论怎样填,都不能使其他两个等式成立。
如果第三个等式填2×3=6,那么还剩下1、4、5、7、8、9,能使第一、二个等式成立。 答案为:

通过例题可以看出,解答填等式的题目,首先要从简单的情况想起,选择合适的突破口。
猜你喜欢
数学小灵通(1-2年级)(2022年12期)2022-12-23
数学小灵通(1-2年级)(2020年9期)2020-10-27
数学小灵通(1-2年级)(2020年5期)2020-06-24
小学生学习指导(低年级)(2020年3期)2020-06-02
新高考·高一数学(2018年5期)2018-11-22
高中生·天天向上(2018年2期)2018-04-14
数学小灵通(1-2年级)(2017年12期)2018-01-23
试题与研究·中考化学(2016年1期)2016-09-30
读写算(中)(2016年9期)2016-02-27
读写算(中)(2015年11期)2015-11-07

