尺度适应性二代小波的图像去噪方法
,,
(武汉理工大学 能源与动力工程学院,武汉 430063)
噪声可以理解为“妨碍人们感觉器官对所接收的信源信息理解的因素”,它是影响图像质量的主要因素。因此,有必要对图像进行去噪处理来提高图像的质量。
小波特有的时频分析能力使其在图像处理领域获得了较好的效果。特别是Mallat和Mayer提出的多分辨分析(MRA)小波理论[1]为图像去噪提供了更理想的工具。一般可以将传统的小波去噪的方法分为三大类[2]:第一类方法是基于小波变换模极大值原理的方法,此方法在去噪过程中存在一个由模极大值重构小波系数的问题,计算量非常大;第二类方法是基于小波系数尺度之间的相关性原理进行图像去噪,需要进行多次迭代,还需估计噪声方差;第三类方法是小波阈值去噪方法,该方法其阈值的选取比较困难,而且阈值的选取还依赖于噪声的方差。
由于传统小波存在上述缺点,第二代提升小波产生,所有的传统小波都可以由提升方法中的基本提升和对偶提升分解而成,提升方法能够包容传统所有的小波。
1 二代小波变换的基本原理
1994年,Swelden[3]提出了一种不依赖于傅里叶变换的新的小波构造方法——提升方法,被称之为第二代小波或整数小波变换。二代小波提升算法的基本原理如下。
1.1 分裂
将一个信号sj分为一个奇数数列与偶数数列,即:split(sj)=(dj-1,sj-1)
(1)
1.2 预测

dj-1=oddj-1-P(evenj-1)=dj-1-P(sj-1)
(2)
1.3 更新(提升)
通过一算子U产生一个新的子数据集sj-1,更新过程可定义为:
sj-1=evenj-1+U(dj-1)=sj-1+U(dj-1)
(3)
对于更新之后的数据子集sj-1再进行上面一样的分裂,预测和更新的过程,经过n次分解后原始数据sj可表示为{dj-n,dj-n+1,…dj-1}。
1.4 重构(反变换)
重构数据过程中的提升公式与分解公式基本相同,区别仅在于计算次序与正负号,可表示为:
sj-1=sj-1-U(dj-1)
dj-1=dj-1+P(sj-1)
sj=Merge(dj-1,sj-1)
(4)
2 二代小波在图像去噪中的应用
在小波变换中,不同的图像存在不同的最佳分解尺度,它们由图像本身的特点所决定,在小波变换中应该根据具体图像来自适应地确定其分解尺度,这样才能得到对该图像更好的分解效果。第二代小波具有非常好的灵活性,通过选择不同的预测算子和修正算子可以得到具有较好的适应性小波变换[4]。尺度适应性算法的原理是要求在图像分解的每一层上,使得预测适应于图像在相应尺度的结构特点。其基本思路是:构造合适的预测滤波器和修正滤波器,使得在每一个尺度下的分解满足优化条件。由此提出一个尺度选择的能量最大差异准则:若所选择的尺度使得所有尺度上分解结果的能量差异达到最大,则所选择尺度就是最佳分解尺度。
(5)
相邻两尺度的能量之差定义为:
(6)
其中上面公式中的k为小波变换的点数。
定义适应度函数用于评价不同尺度分解效果:
(7)
式中的1,2…,j为待选尺度。如果F(1,2…,j)为最大值,则j-1为最佳分解尺度。
根据噪声在小波变换域中的特征知道,噪声的强度随着分解尺度J的增大而降低[5],如果在各个尺度上使用相同全局阈值λ,虽然可使计算简单,但在一定程度上“过扼杀”了小波系数的倾向。所以对噪声图像做尺度适应性二代小波变换后,对每一层的细节信号部分(即高频部分)都要进行阈值处理,传统的硬阈值函数可以很好保留图像边缘的局部特征,但重构后的图像会产生一些振荡或纹理不清晰等现象,而软阈值函数处理结果相对平滑得多,但会造成边缘模糊等失真现象。基于以上软硬阈值的不足,本文采用改进的阈值函数来进行阈值处理,改进的阈值函数定义如下:
式中,μ∈R,并且μ>1.0.
(8)
(9)
β=dj-J/(dj-J+Si-J)
(10)
(11)
很容易看出当|WJ,(j,k)|≥λ,
(12)
(13)
(14)
从上面的(14)(15)式中可以看出,当μ→∞,式(14)正是经典的硬阈值法,而当μ→1,式(15)是经典的软阈值法。所以上面(9)式提出的改进的阈值算法可以很好的折中软硬阈值。
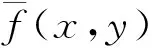
对于图像中的噪声来说,噪声的小波系数值随分解层数J增加而减小。所以(12)式中λ与J的取值成反比。
根据上面收缩阈值函数对分解后的每一层的高频部分进行处理后,高频系数中的噪声部分得到极大的消减,然后由处理后的高频部分与正变换得到的低频部分在每一层上根据上面(4)式给出的重构方法重新得到新的图像。
为了衡量图像去噪性能评价标准,我们常用信噪比来测量图像噪声量,这种方法常被用来作为图像去噪效果评价的指标。信噪比单位是分贝(db),其定义为:
SNR=10×log10(powerimage/powernoise)
(15)
(16)
如果去噪后的图像信噪比SNR值越大,则图像去噪效果就越好。
3 实验分析与结论
为了验证提出的二代小波对噪声图像去噪的效果,本实验选取噪声图像进行二代小波变换后按照尺度适应性算法进行阈值处理,处理后效果图对比见图1~5及表1。

图1 噪声图像

图2 二维中值滤波

图3 小波软阈值去噪

图4 小波硬阈值去噪

图5 尺度适应性二代小波去

表1 不同去噪效果信噪比(SNR)对比
通过实验可以很明显地看出尺度适应性二代小波对图像去噪效果更好,去噪后图像的信噪比大大地提高、更加清晰、边缘与纹理信息也更加丰富。
第二代小波变换是对传统小波理论的进一步发展,研究还在起步阶段,其理论研究尚需要进一步深入。
[1] Gonzalez R C, Woods R E, Eddins S L.Digital Image Processing Using Matlab[M].Beijing: publishing House of Electronics Industry, 2005.
[2] 赵瑞珍.小波理论及其在图像、信号处理中的算法研究[D].西安:西安电子科技大学,2001.
[3] Sweldens W.The lifting scheme: a custom-design construction for biorthononal wavelets[C].University of South Carolina, 1994:1-39.
[4] 王志武,丁国清,颜国正,等.自适应提升小波变换与信号去噪[J].计算机工程与应用,2002(2):28-30.
[5] 谢荣生,李汉杰,孙 枫,等,基于多小波噪声方差阈值的信号滤波方法[J].哈尔滨工业大学学报,2002,23(2):51-54.

