从一道探索题折射学生的思维和创新能力
曾炳文
义务教育阶段的《数学课程标准》明确规定学生在数学学习中的各种目标,其中之一是要求学生经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,能有条理地,清晰地阐述自己的观点。下面以本人课堂教学中的一道探索题为例加以阐述。以折射出同学们的发散思维能力和创新能力,从而发映我们要追求的课堂教学景观。
例:观察下列正方形图案,每条边上有n(n≥2)个圆点,每个图案中圆点的总数是S。

n=2,S=4n=3,S=8n=4,S=12……
按此规律推断出S与n的关系式。
此问题一在课堂上展现,立即引起同学广泛的兴趣。同学们跃跃欲试,纷纷想发表自己的见解。在经过小组合作、思考、讨论后,各小组选派一位同学发言。同学A说,S=4n-4,理由是:正方形每条边上的圆点个数有n个,那么4条边上共有4n个圆点,扣除4个顶点重复计算各一次,结果有(4n-4)个。他的敏捷思维和流畅的表达得到大家的一致赞许。紧接着同学B说,S=4(n-1)。随后她自信地走上讲台,在黑板上刷刷地把每个正方形的圆点分成四个部分(如图(1)所示)。
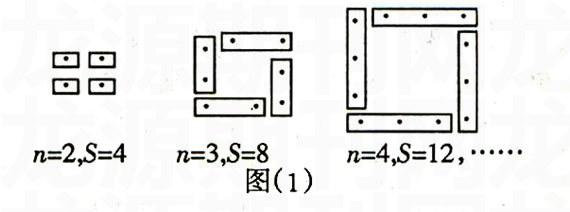
她发现每部分的圆点数比每条边的圆点数少1个且数目相同,结果总数为S=4(n-1)。在同学B的启示下,学生的思维火花得到充分绽放。紧接着,同学C也上台说,S=2n+2(n-2),并在黑板上画出示意图(如图(2)所示)。

他的理由是:上、下两条边中每条边各有n个圆点,共2n个。中间每行有2个点,且行数比n少2,结果有2(n-2)个,所以总数S=2n+2(n-2)个。同学D说,正方形是中心对称图形,被图中虚线分开的两部分的圆点数一样(如图(3)所示),且每部分均为n+(n-2),所以总数为S=2[n(n-2)]。
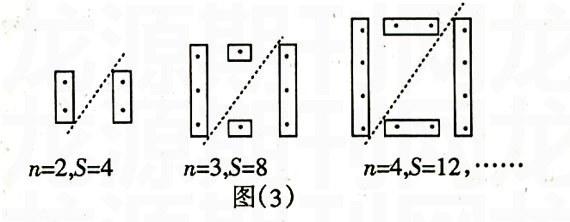
同学E说,正方形也是一个轴对称图形,能否从轴对称角度来考虑,经过几分钟的思考,他说,S=2[1+2(n-2)]+2(如图(4)所示)

理由是:被图中虚线分开的每部分圆点数是1+2(n-2),根据图形对称性,再加上虚线上的两个点,所得总点数S=2[1+2(n-2)]+2。至此,同学的积极性已发挥得淋漓尽致,大家都在积极思考与众不同的解法。忽然同学F说,老师我还有一种想法,如果把正方形里面的空洞按规律放上圆点,让行、列的圆点数一样,则每个正方形的圆点个数为n2个,而放上的中间正方形的圆点个数为(n-2)2个,所以结果S=n2-(n-2)2。这时,全班同学报以热烈的掌声。这位同学脸上也露出了自豪的微笑。
正当大家为同学F叫好的时候,也许是受课堂热烈气氛的感染,班上一位平时比较腼腆的同学举了手说,老师,我发现S是4的倍数,只要把数据分析一下可以看出,当n=2时,S=4=4×2-4;
当n=3时,S=8=4×3-4;
当n=4时,S=12=4×4-4;
不难发现,S=4n-4。
由此可见,课堂良好的氛围对同学潜移默化的影响是多么大啊!
这时有的同学说,老师,怎么它们的结果的书写表达式不一样呢?在老师的适当引导下,同学们明白经过适当的化简、整理,结果都可以写成S=4n-4,正好验证一句成语一殊途同归。
本节探讨的是“归纳—猜想”型题目。这种题目的命题形式是:结合几个具体的、特殊的数、式或图形,要求找出其中的变化规律,从而猜想出一般性的结论。它的解题基本思路是:从特殊向一般的转化。它的具体做法是:(1)归纳:通过对几个特例的分析,寻找规律并加以归纳;(2)猜想:猜想符合规律的一般性结论;(3)验证:验证或证明结论是正确的。
通过本节课的教学,我深深地体会到,只要课堂上尽可能多地提供学生自主、宽松的学习时空和合作交流的学习机会,课堂必然会焕发出生机勃勃的活力。教师要改变以例题、示范、讲解为主的教学方式,引导学生投入到探索与交流的学习活动中,使学生享有广阔的思维空间,从而迸发出创新的火花。

