基于参数随机分布的潜流带地下水数值模拟研究

摘 要：含水层水文地质参数的合理性是决定地下水数值模型模拟精度的关键因素之一。以淮河流域清水河典型河段为研究区，通过含水层土体野外监测和室内试验，建立了渗透系数、给水度和贮水率的概率密度分布函数，并利用参数中值和置信度为95%的置信区间，建立了基于多参数概率密度分布的地下水数值模型。结果表明：相较于采用地质勘探建议值的传统地下水数值模型，基于多参数概率密度分布的地下水数值模型的地下水位模拟结果的精确度得到了显著提升；河流水位、河床渗透系数等直接影响河流与地下水之间的水量交换强度，以及地下水的渗流和储存特征。

关键词：地下水；数值模拟；参数随机分布；清水河

中图分类号：TV62；TV882.1 文献标志码：A doi：10.3969/j.issn.1000-1379.2025.02.016

引用格式：王辉，刘军生，王荆，等.基于参数随机分布的潜流带地下水数值模拟研究[J].人民黄河，2025，47（2）：107-112，155.

基金项目：引江济淮工程（河南段）工程科研服务项目（HN-YJJH/JS/FWKY-2021001）；黄河水利科学研究院基础研究业务费专项（HKY-JBYW-2023-07）；水利部堤防安全与病害防治工程技术研究中心开放课题（LSDP202402）

NumericalSimulationofGroundwaterinSubsurfaceFlowZoneBasedonRandom DistributionofParameters

WANGHui1，LIUJunsheng2，3，WANGJing2，3，4，ZHAOShougang2，3，SUNRuidong2，3，WANGTianye4，ZHANGYibo2，3，LANYan2，3，YANGHaoming2，3，HOUJiaojian2，3

（1.HenanYangtze？to？HuaiheWaterDiversionCo.，Ltd.，Shangqiu476200，China；2.YellowRiverInstituteofHydraulicResearch，YRCC，Zhengzhou450003，China；3.ResearchCenteronLeveeSafetyandDisasterPrevention，MWR，Zhengzhou450003，China；4.SchoolofWaterConservancyandTransportation，ZhengzhouUniversity，Zhengzhou450001，China）

Abstract：Thereasonablenessofaquiferhydrogeologicalparametersisoneofthekeyfactorstodeterminethesimulationaccuracyofgroundw？ aternumericalmodels.Takingthetypicalcross？sectionoftheQingshuiRiverintheHuaiheRiverBasinasthestudyarea，theprobability densitydistributioncharacteristicfunctionsofthepermeabilitycoefficient，thedegreeofwatersupplyandtherateofwaterstoragewereestab？ lishedthroughthefieldmonitoringofaquifersoilsandindoorexperiments，andthenumericalgroundwatermodelbasedonthemulti？parame？ terprobabilitydensitydistributionwassetupbyusingthemedianvalueoftheparameterandtheconfidenceintervalwithaconfidencelevelof 95%.Theresultsshowthattheaccuracyofthegroundwatersimulationresultsofthegroundwaternumericalmodelbasedonmultiparameter probabilitydensitydistributionissignificantlyimprovedcomparedwiththetraditionalgroundwaternumericalmodelusingthesuggestedvalues ofgeologicalexploration.Thedifferentsimulationscenarios，suchastheriverlevelandthepermeabilitycoefficientoftheriverbed，directly affecttheintensityofwaterexchangebetweentheriverandthegroundwater，aswellastheseepageandstoragecharacteristicsoftheground？ water.

Keywords：groundwater；numericalmodeling；parameterstochasticscheme；QingshuiRiver

0 引言

潜流带作为地表水和地下水相互作用最强的区域，水量相对丰富和稳定，其水文动态对水资源评估、开发和管理具有重要影响。此外，潜流带孕育的河岸生态系统具有重要生态功能和价值，尤其在干旱地区[1]。水文地质参数是表征含水层或含水层介质渗透性、储水或释水特性的指标，是模拟地下水定量运移的关键参数。潜流带地层沉积环境复杂[2]，水文地质参数具有很强的空间异质性，表现为大尺度的随机分布[3-4]。为了描述水文地质参数的空间异质性，有学者基于参数随机分布理论，探讨了参数统计特征与概率密度分布函数之间的关系。随机场理论最初由Vanmarcke[5]于1977年提出，此后被广泛应用于描述岩土参数的空间分布特征。近年来，描述土壤空间自相关特性的随机场模型得到了广泛应用。Srivastava等[6]采用随机有限元法模拟了土壤渗透系数的随机场，结合蒙特卡罗模拟方法，研究了渗透系数的空间变化对边坡渗流和边坡安全系数的影响；Santoso等[7]利用局部平均法对土壤渗透系数的随机场进行了离散化处理；Zhu等[8]采用快速傅里叶变换方法模拟了渗透系数的空间变化；Cho[9]通过蒙特卡罗模拟方法，研究了渗透系数的空间异质性对土石坝渗流和渗流梯度均值、方差等统计特征参数的影响。

虽然学者们对岩土参数的随机场理论进行了大量研究，但相关研究成果的实际应用主要是在工程地质和边坡稳定性领域。在地下水数值模拟中，通常给含水层指定一个固定参数，往往忽略了其空间异质性和频率分布特征。Tang等[10]发现，河床水文地质参数的随机分布极大地影响了地下水数值模拟的精度，这表明传统的均质含水层假设在研究小尺度、高精度的透水带方面存在局限性。本研究以淮河流域清水河典型河段野外监测和室内试验为基础，通过颗粒分析试验，对土样进行分类，并将地质调查获得的土壤参数与实验室土壤水力性质测试结果相结合，建立渗透系数、给水度和贮水率的概率密度分布模型。同时，基于建立的MODFLOW地下水数值模型，分析参数随机分布对地下水数值模拟精度的影响，探究地下水在含水层非均质情况下的运移规律。

1 数据与方法

1.1 研究区概况

研究区位于引江济淮工程清水河河段，引江济淮工程沟通长江、淮河两大水系，润泽安徽、惠及河南、造福淮河、辐射长江，具有保障供水、发展航运、改善水环境等综合效益。研究区属黄淮冲积平原，清水河全长137.3km，流域面积901km2，属暖温带半湿润大陆性季风气候区，气温、降水和风向随季节变化。年平均降水量为720～820mm，降水集中在6—9月，通常占全年降水量的70%以上。上游年蒸发能力1200～1400 mm，中下游则达1866mm。数值模拟区位于清水河河段重点监测断面16。地下水类型为第四系松散层孔隙潜水，主要赋存于砂壤土、轻粉质壤土及粉细砂层内，下部粉细砂层中地下水具有承压性，砂壤土、粉细砂、轻粉质壤土具有中等透水性，重粉质壤土具有弱透水性（为相对隔水层）。

1.2 数据收集和监测

研究区内河道沿线的水文地质条件、工程地质条件及数字高程模型（DEM）由《引江济淮河南省受水区供水配套工程可行性研究阶段工程地质勘察报告及图册》与现场地质钻孔数据综合分析得出，下垫面条件主要通过卫星遥感影像与现场无人机航拍获取。通过ArcGIS软件生成研究区DEM数据，为地下水数值模拟提供准确的地表数据。

为获取地层渗透系数空间分布特征，沿水平纵横向布设3×3个地下水监测及试验钻孔，见图1。同时，在监测孔取样，垂直向揭露透水砂层，每孔按垂直深度间距0.5～1.0m取样，分层采集试验土样，每层土样开展密度、颗粒分析、给水度及渗透系数等试验。

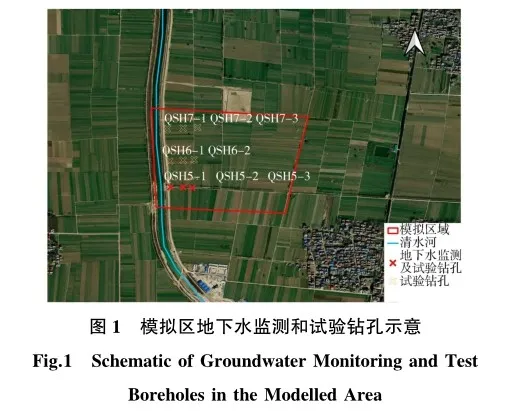
为了研究河流与地下水之间的相互作用关系，在距离河道50、100、150m处分别设置自动化水位监测井。这些监测井采用VWP-0.35G型地下水位传感器，每24h监测1次。鉴于农田是研究区域的主要土地利用类型，且附近有大量灌溉机井，因此除自动化水位监测井外，通过人工巡查的方式定期评估周边地区的地下水开采活动。

1.3 数学模型

由于目前的勘察技术无法准确获取研究区的水文地质条件，因此使用地下水运动数学模型来表达复杂的水文地质体，建立数学公式来表达水文地质条件与相关参数的函数关系。可用下列数学模型描述潜水水流运动：

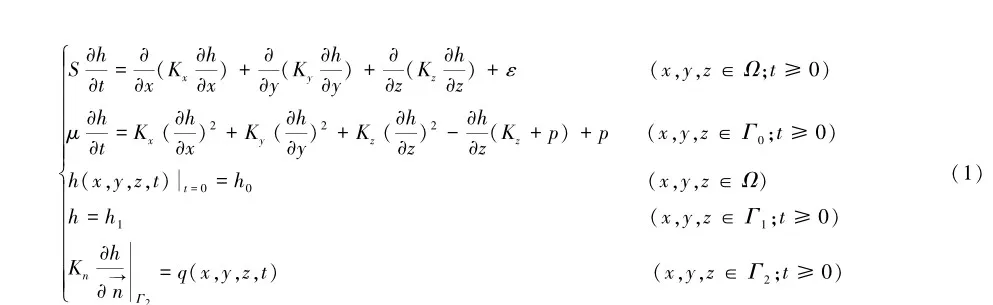
此数学模型利用VisualMODFLOWFlex中的有限差分法求解。

1.4 随机统计方法及随机参数分析理论

随机变量可以分为离散型和连续型两类。常见的连续分布密度函数包括均匀分布、指数分布、正态分布、t分布等。在统计和概率论中，均匀分布是一种常见的概率分布，随机变量均匀分布指在一定区间内，随机变量每个值出现的概率都是相同的；指数分布具有无记忆性，是特殊的伽马分布；正态分布是一种极为常见的连续型概率分布，均值μ决定了分布的位置，标准差σ决定了分布的幅度和形状；t分布用于根据小样本来估计呈正态分布且方差未知的总体的均值，如果总体方差已知或者样本数量足够多，则可以用正态分布来估计总体均值。

通过单样本K-S检验法检验样本是否来自于特定的理论分布，单样本K-S检验的判断标准为显著性。

1.5 模型精度评估

采用纳什效率系数SNSE、均方根误差SRMSE对地下水运移数值模型精度进行评估。纳什效率系数计算公式为

2 地下水数值模型的构建

对研究区边界条件进行概化，西边界以清水河为界，水头边界根据清水河水位设定；模型南北跨度为650m，南北边界垂直于河流方向，考虑地下水流的特点，将其定为零流量边界；东边界由序列化监测井划定为给定水头边界。根据钻孔披露的信息，研究区主要由淤泥质黏土、重淤泥质壤土和壤土组成，黏土和砂质壤土呈薄层或透镜状分布，在垂直方向上模型含水层分为4层。

考虑计算工作量和精度要求，将模型空间分辨率设定为5m，模拟时间步长设定为1d。模型被细分为121行、185列，共22385个矩形网格单元，计算节点位于网格单元中心。地下水数值模型模拟时间从2022年8月26日开始，时间跨度为8个月。

2.1 水文地质参数

研究区水文地质参数具有空间异质性，通过对试验结果进行统计分析，可以得到相关参数的概率密度分布函数。第一层含水层为重粉质壤土，垂直渗透系数服从指数分布，水平渗透系数和给水度服从t分布，贮水率符合指数分布。由于这些参数在数量级上存在较大差异，因此采用对数变换进行统计分析，结果见图2。

根据不同土层渗透系数、给水度、贮水率概率密度分布曲线，得出各土层渗透系数、给水度和贮水率地质勘探建议值、中位数和置信度为95%的置信区间，见表1。

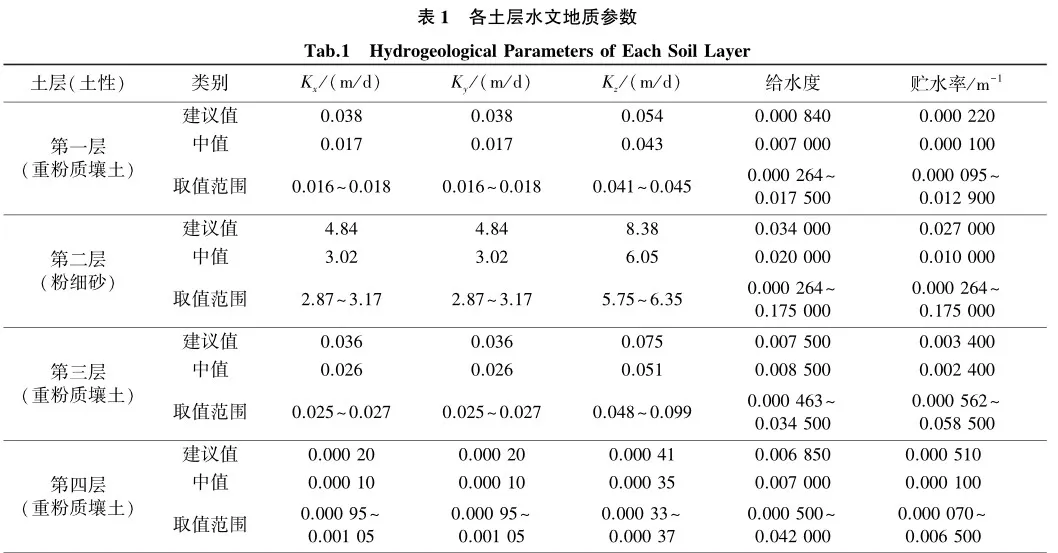
2.2 源汇项的确定和处理

模型中地下水运动主要受汇源项输入的影响，模拟区源汇项有点、线、面3种要素。点状要素为农业开采等源汇项；线状要素主要为河流补给项，通过River模块处理；面状要素主要为降雨入渗、灌溉入渗等补给项，由Recharge模块给出。潜水蒸发等其他源汇项资料通过Well模块代入模型计算，均处理成开采井或者补给井。

2.3 初始条件

由于研究区水文地质资料不足，因此无法直接获得初始流场。根据已有DEM数据、降雨资料、流域流入和流出数据，以及研究区各含水层水文地质参数，模拟2022年地下水流场稳定流，获得稳定流初始流场。

2.4 数值模型

根据水文地质概念模型，将水文地质参数及其他边界条件输入模型，基于土体参数空间随机分布理论中参数分区与取值方法，针对模拟区水文地质条件和源汇项特征，利用初始条件和边界条件对地下水流动微分方程组进行求解，得到研究区地下水流场数值模型，地质结构与水位分布见图3。

3 模型验证与识别

3.1 模型验证

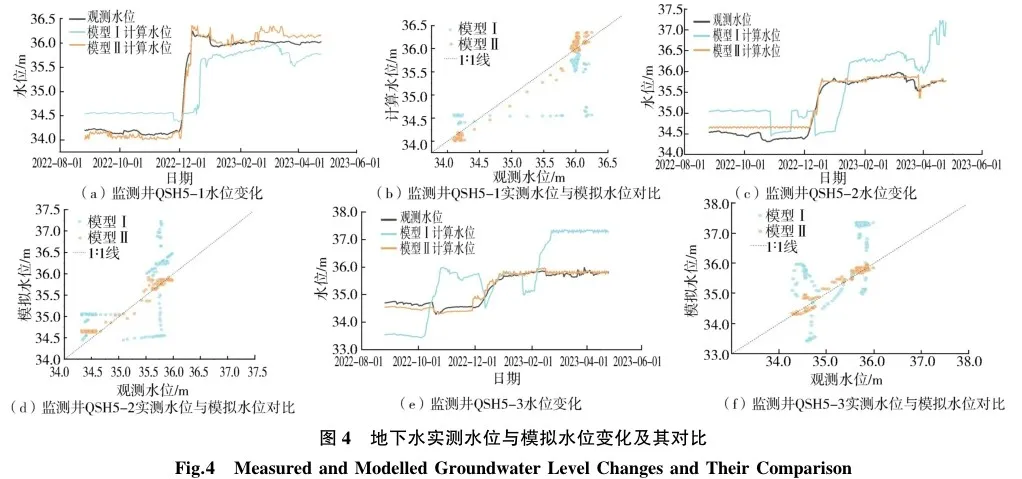
为探究多参数概率密度分布在构建地下水数值模型方面是否具有优势，建立了两组地下水数值模型。两组模型保持边界、源汇项、时间步长等条件不变，模型Ⅰ作为对照组，采用地质勘探建议的水文地质参数（平均值）；模型Ⅱ将参数中值作为初始模型参数，同时将95%置信区间作为参数反演范围。使用Visual MODFLOWFlex中内嵌的PEST反演模块对模型参数进行校准，最终确定模型参数。2022年8月24日至2023年2月24日为模拟期，2023年2月24日至2023年4月24日为验证期，模型Ⅰ和模型Ⅱ模拟的部分钻孔的地下水位与实测水位见图4。

模型Ⅰ对QSH5-1、QSH5-2、QSH5-3的水位计算值相对于实测值的均方根误差分别为0.47、0.65、1.13 m，确定系数R2分别为0.47、0.59、0.22，纳什效率系数分别为0.73、0.02、-2.96。模型Ⅱ对QSH5-1、QSH5-2、QSH5-3水位计算值的均方根误差明显较小，分别为0.13、0.16、0.14m；R2显著提高，分别为0.81、0.76、0.77；纳什效率系数显著增大，分别为0.98、0.94、0.94。比较模拟水位与实测水位可知，模型Ⅰ计算水位与实测水位最大差值出现在2022年10月24日QSH5-3处，差值为127cm，最小差值出现在2023年1月24日QSH5-3处，差值为69cm；模型Ⅱ计算水位与实测水位最大差值出现在2022年10月24日QSH5-3处，差值为27cm，较模型Ⅰ降低了78.7%，最小差值出现在2022年12月24日QSH5-2处，差值为0.9cm，较模型Ⅰ降低了98.7%。因此，考虑参数随机分布的地下水数值模型计算结果与实测值更接近，模型拟合效果更好。

3.2 农田输水过程中地下水流场的动态变化

清水河2022年11月15日首次通水后，研究区地下水位受河道补给影响显著，其中距离河道约50m处的观测孔QSH5-1地下水位由34.389m（2022年12月2日）上升到最高水位36.160m（2022年12月18日），16d抬升1.771m；距离河道约100m处的观测孔QSH5-2地下水位由34.554m（2022年12月5日）上升到最高水位35.667m（2023年1月5日），31d抬升1.113m；距离河道约150m处的监测井QSH5-3地下水位由34.651m（2022年12月9日）上升到最高水位35.708m（2023年2月19日），72d抬升1.057m。

根据监测结果可知，通水后地下水流场由周边农田补给河道转换为河道补给周边农田；由于各监测井与河道距离不同，因此其地下水位变化也存在较大差异。河道补给地下水存在一定滞后性，以监测井QSH5-1、QSH5-3为例，垂向水位变化速率分别为0.295、0.015m/d，距离河道较近处地下水受河道补给影响远大于距离河道较远处的。

3.3 不同输水条件下地下水流场变化

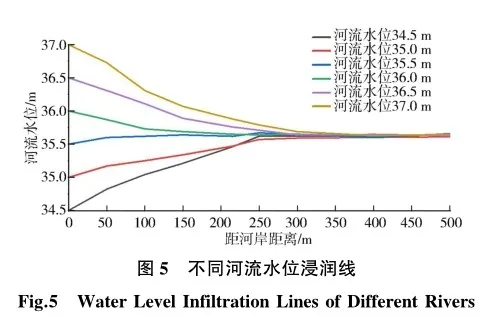
基于上述反演校正后的地下水数值模型，以模拟期第80d为例，分别把河流水位34.5、35.0、35.5、36.0、36.5、37.0m输入模型，对比分析河流水位变化对地下水流场的影响，不同河流水位浸润线见图5。当河流水位≤35.5m时，周边农田地下水补给河流；当河流水位>35.5m时，河流补给地下水，地下水位在距离河道150～300m处逐渐趋于平稳。其中，河流水位为35.5～36.0m时，河流对地下水位的影响较小，地下水位在距离河道约100m处已趋于平稳；河流水位为36.5～37.0m时，河流补给地下水，且河流对地下水位影响距离较远，地下水位在距离河道250～400m处趋于平稳。

3.4 河床渗透系数对河流渗流量的影响

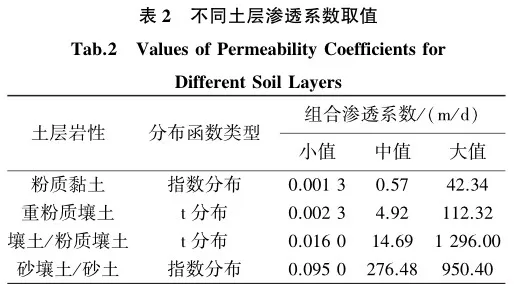
分别选取各地层概率密度分布函数中渗透系数置信区间95%的小值、中值及大值组合（见表2），利用VisualMODFLOWFlex建立地下水数值模型，模拟计算河道正常调度水位条件下，河道运行期单侧年渗流量。计算结果表明，最大、最小渗流量分别为57.2万、25.2万m3，渗流量变幅是最小渗流量的126.9%，由此可见河床渗透系数随机性对河流渗流量影响十分显著。

4 结论

基于清水河典型河段含水层土体野外监测和室内试验，分析了渗透系数、给水度和贮水率等水文地质参数变化，并建立了渗透系数、给水度和贮水率的概率密度分布函数，利用参数中值和置信度为95%的置信区间，建立了基于多参数概率密度分布的地下水数值模型，并将该模型与采用地质勘探建议值的传统地下水数值模型模拟结果进行了对比。结果表明，相较于采用地质勘探建议值的传统地下水数值模型，基于多参数概率密度分布的地下水数值模型的模拟水位与实测水位的最大差值比传统模型降低了78.7%，最小差值比传统模型降低了98.7%，模型模拟结果精确度明显提升。

将基于多参数概率密度分布的地下水数值模型计算结果与实测水位进行比较，在相同外部条件下，当河流水位增大至35.5m以上时，研究区潜水带由地下水补给河流转换为河流补给地下水；河床渗透系数由最小值增大到最大值时，河流单侧年渗流量从25.2万m3增加到57.2万m3，渗流量变幅是最小渗流量的126.9%。这说明河流水位、河床渗透系数等直接影响河流与地下水之间的水量交换强度，以及地下水的渗流和储存特征。

参考文献：

[1] WANGTianye，WUZening，WANGPing，etal.Plant？Ground？ waterInteractionsinDrylands：AReviewofCurrentResearch andFuturePerspectives[J].AgriculturalandForestMeteorol？ ogy，2023，341：109636.

[2] 刘鑫，王宇，李典庆.考虑土体参数空间变异性的边坡大变形破坏模式研究[J].工程地质学报，2019，27（5）：1078-1084.

[3] 纪文贵，罗跃，刘金辉，等.考虑渗透系数不确定性的地浸过程溶浸范围随机模拟[J].原子能科学技术，2023，57（6）：1099-1110.

[4] 张俊，刘天罡，董佳秋，等.含水层层状非均质对地下水流系统的影响[J].中国地质，2020，47（6）：1715-1725.

[5] VANMARCKEEH.ProbabilisticModelingofSoilProfiles[J].JournaloftheGeotechnicalEngineeringDivision，1977，103（11）：1227-1246.

[6] SRIVASTAVAA，BABULSG，HALDARS.Influenceof SpatialVariabilityofPermeabilityPropertyonSteadyState SeepageFlowandSlopeStabilityAnalysis[J].Engineering Geology，2010，110（3-4）：93-101.

[7] SANTOSOAM，PHOONKK，QUEKST.EffectsofSoilSpa？ tialVariabilityonRainfall？InducedLandslides[J].ComputersStructures，2011，89（11）：893-900.

[8] ZHUH，ZHANGLM，ZHANGLL，etal.Two？Dimensional ProbabilisticInfiltrationAnalysiswithaSpatiallyVarying PermeabilityFunction[J].ComputersandGeotechnics，2013，48：249-259.

[9] CHOSE.ProbabilisticAnalysisofSeepageThatConsiders theSpatialVariabilityofPermeabilityforanEmbankmenton SoilFoundation[J].EngineeringGeology，2012，133：30-39.

[10] TANGQ，KURTZW，SCHILLINGOS，etal.TheInfluence ofRiverbedHeterogeneityPatternsonRiver？AquiferEx？ changeFluxesUnderDifferentConnectionRegimes[J]. JournalofHydrology，2017，554：383-396.

【责任编辑 吕艳梅】