阶梯水价框架下黄河流域城市居民用水权交易策略研究

摘 要：为了解决黄河流域生产、生活、生态用水矛盾突出问题，缓解水资源对经济社会发展和生态环境的约束，构建了城市居民用水权交易博弈模型，分类分析了缺水居民在用水权交易中的策略选择，探究了余水居民策略选择的稳定性以及策略改变的速度，最后以河南省郑州市为例，运用Matlab软件进行数值仿真。结果表明：1）余水居民A与缺水居民B1、缺水居民B2均可达成用水权交易。2）随着时间衰减因子的增加，余水居民A和缺水居民B1的策略变化速度先减小后增大。3）缺水居民B2的策略选择与余水居民A和缺水居民B1有关。制定合理的用水权交易机制有助于激励居民节约用水。

关键词：用水权交易；阶梯水价；演化博弈；城市居民；黄河流域

中图分类号：TV213.4；TV882.1 文献标志码：A doi：10.3969/j.issn.1000-1379.2025.02.011

引用格式：王延荣，任苏明.阶梯水价框架下黄河流域城市居民用水权交易策略研究[J].人民黄河，2025，47（2）：74-80，94.

基金项目：河南省科技厅软科学项目（242400411060）；国家社会科学基金资助项目（23BJY062）

StudyontheTradingStrategyofUrbanResidents’WaterRightsinthe YellowRiverBasinUndertheFrameworkofLadderWaterPrice

WANGYanrong1，2，RENSuming1

（1.SchoolofManagementandEconomics，NorthChinaUniversityofWaterResourcesandElectricPower，Zhengzhou450046，China；2.CivilWaterLiteracyResearchCenter，NorthChinaUniversityofWaterResourcesandElectricPower，Zhengzhou450046，China）

Abstract：Inordertosolvetheoutstandingcontradictionofwateruseforproduction，livingandecologyintheYellowRiverBasin，andtoal？ leviatetherigidconstraintsofwaterresourcesoneconomicandsocialdevelopmentandecologicalenvironment，thispaperbuiltagamemodel ofurbanresidents’waterrightstrading，classifiedandanalyzedthestrategychoicesofwater？scarceresidentsinwaterrightstrading，explored thestabilityofthestrategychoicesofwater？scarceresidentsaswellasthespeedofstrategychange，andfinallyconductednumericalsimula？ tionbyusingMatlabsoftware.Theresultsshowthata）ResidentAwithsurpluswaterandResidentB1andResidentB2withwatershortage canreachawaterrighttransaction.b）Withtheincreaseoftimedecayfactor，thespeedofstrategychangeofresidualwaterResidentAand watershortageResidentB1decreasesandthenincreases.c）ThestrategychoiceofwatershortageResidentB2isrelatedtoresidualwater ResidentAandwatershortageResidentB1.Therefore，thedevelopmentofareasonablewaterrighttradingmechanismcanhelptostimulate residentstosavewater.

Keywords：waterrightstrading；ladderwaterprice；evolutionarygame；urbanresident；YellowRiverBasin

0 引言

长期以来，黄河流域水资源紧缺，人均水资源占有量不到全国平均水平的30%。在城市广泛实施的居民用水阶梯水价政策为推动节水发挥了重要作用。调查发现，一部分居民用水比较节约，其用水量在水价第一阶梯内尚有少量剩余；另一部分居民用水量达到水价第二阶梯，甚至有很少一部分达到水价第三阶梯。因此，在城市居民用水管理中开展用水权交易成为一种有效激励用户节水的重要手段。现有研究中，张保林[1]构建城市居民需求方用水权交易模型，发现在城市供水系统中利用市场进行生活用水量配置可以提高居民的节水意识。Schmack等[2]认为大规模的混合供水系统是水交易市场建立的基础。总量控制和定额管理为城市用水权交易提供了管理框架，超定额累进加价制度和阶梯水价制度为城市居民用水权交易提供了基础条件。

博弈定价方法在用水权交易方面有很好的应用效果，双层动态博弈模型可以确定水权最优交易量与价格之间的关系[3]，竞价拍卖贝叶斯模型可以给出多主体交易水权的最优交易方案[4]，演化博弈可以对用水权交易的相关参数进行系统分析[5]，合作博弈能保证用水权交易的公平性[6]。

目前，居民可以通过节约用水来获得节水奖励，通过交易剩余用水权而获得节水收益是城市居民节水管理的重要措施之一，已经逐步引起有关方面的重视。因此，本文以黄河流域城市居民为交易主体，在水权权属明晰后，建立用水权交易价格演化博弈模型，分析用水权交易活动中各参与主体的出价策略，聚焦参与主体策略选择，研究不同类型的居民参与用水权交易的积极性，以期为水行政主管部门建立用水权交易平台、制定合理的用水权交易价格和激励用水户积极参与用水权交易提供参考。

1 问题描述与模型假设

1.1 问题描述

在水资源短缺的背景下，将用水权交易引入城市居民用水管理的原因主要有两个：一是国家提出运用经济手段倒逼居民节水的政策思路，除通过制定具有影响力和约束力水价促进居民节水外，通过用水权交易优化城市居民水资源配置也是一种重要的制度设计[7]；二是目前基于阶梯水价框架的居民用水计费制度设计中实行分类计量收费和超定额累进加价，其设计理念是通过对多用水者的经济“惩罚”倒逼居民节水，而将用水权交易引入城市居民用水管理中，实际上是通过对用水少者的经济“奖励”调动城市居民节约用水的积极性。

根据参与用水权交易双方的用水量不同，将在第一阶梯水价中有剩余水量的居民定义为余水居民A，将用水量超过第一阶梯水价水量的城市居民定义为缺水居民（用水量超过第一阶梯但未超过第二阶梯的记为缺水居民B1，用水量超过第二阶梯的记为缺水居民B2）。当缺水居民的用水量超过第一阶梯水价水量时有两种选择：一是直接使用第二、第三阶梯水量，二是通过向余水居民购买用水权获得用水量。城市居民用水权交易可以分为两种情形：一是余水居民A与缺水居民B1进行用水权交易，二是余水居民A与缺水居民B1、缺水居民B2进行用水权交易。同时，余水居民需要对是否转让用水权做出选择。因此，在政府监管以及用水需求增加的情况下，用水权交易双方具体的交易行为随之出现。本文研究余水居民和缺水居民的用水权交易行为决策问题，其中：余水居民决策是否转让用水权，缺水居民决策是否接受报价。

1.2 模型假设

在阶梯水价框架下，政府可以根据缺水居民的类型确定用水权交易价格区间，即缺水居民B1用水权交易价格区间的下限为第一阶梯水价，上限为第二阶梯水价。同理，缺水居民B2参与用水权交易价格区间的下限为第一阶梯水价，上限为第三阶梯水价。在定价区间内，用水权交易双方就实际交易价格进行讨价还价。

假设1：用水权交易价格博弈的余水居民和缺水居民双方均为有限理性的，都不希望交易失败，都希望能获得较大收益，其策略选择随博弈的进行逐渐稳定于最优策略。

假设2：余水居民A选择转让用水权的概率为x∈[0，1]，选择保留用水权的概率为1-x；缺水居民B1选择接受余水居民报价的概率为y∈[0，1]，选择拒绝报价的概率为1-y；缺水居民B2选择接受余水居民报价的概率为z∈[0，1]，选择拒绝报价的概率为1-z。

假设3：交易失败发生的概率近似服从参数为λ（λ>0）的泊松分布，交易持续时间服从参数为λ的指数分布（λ为单位时间内交易失败发生的平均次数）。在长度为Δ的时间段内，交易失败的概率为1-e-λΔ。

假设4：缺水居民B首先提出报价PB，若余水居民A接受，则交易达成；反之，则由余水居民A提出报价PA。双方轮流出价，余水居民希望价格越高越好，缺水居民希望价格越低越好，显然有PA>PB>0。余水居民能够接受的最低心理价格为WA，缺水居民能够接受的最高心理价格为WB，显然有PB2>PB1、WA2>WA1（下标A1、B1分别表示以第一阶梯用水量交易的余水居民、缺水居民，A2和B2表示以第二阶梯用水量交易的余水居民、缺水居民）。

假设5：谈判时间对用水权交易的影响用时间衰减因子δ（0<δ≤1）表示。时间衰减因子与参与者的耐心有关，且随着时间延长可能有外部竞争者参与，导致原先的用水权交易失败。博弈参与方为交易谈判所付出的相关成本为常量c（c>0），该成本无论交易成败都会产生。

2 用水权交易博弈模型构建与分析

2.1 模型构建

2.1.1 缺水居民B1与余水居民A1的用水权交易

当余水居民A1和缺水居民B1进行交易时，双方收益期望矩阵见表1。

由x*、y*的表达式可以得到结论1：缺水居民B1策略的稳定性由余水居民在交易过程中认为交易失败出现的可能性决定；余水居民策略的稳定性由缺水居民B1认为交易失败出现的可能性、余水居民的心理价格以及双方出价共同决定。

在用水权交易过程中，交易双方会根据对方的出价不断修正自己的策略。由此可以得到结论2：当余水居民通过学习调整自己的策略，使得自己转让用水权的概率趋近于演化稳定策略时，缺水居民B1会根据余水居民的想法调整自己接受报价的概率，使其趋近于稳定状态。当余水居民对自己的报价过于自信而偏离均衡点时，缺水居民B1会为了达成用水权交易而调高自己接受报价的可能性，使之偏离均衡点y*。当缺水居民B1降低接受报价的概率，余水居民会意识到缺水居民B1对于达成用水权交易的意愿不强，则会随之降低自己转让用水权的概率，使之偏离均衡点x*。当缺水居民B1调高自己的报价时，余水居民会对自己的策略进行调整，增大选择转让用水权的概率，使其达到演化稳定策略。

2.1.2 缺水居民B1、B2与余水居民A的用水权交易

当余水居民A、缺水居民B1和B2参与水权交易时，三方收益期望矩阵见表2（若B1、B2均选择接受余水居民报价，则A与B2交易时收益较高，A将与B2达成交易）。

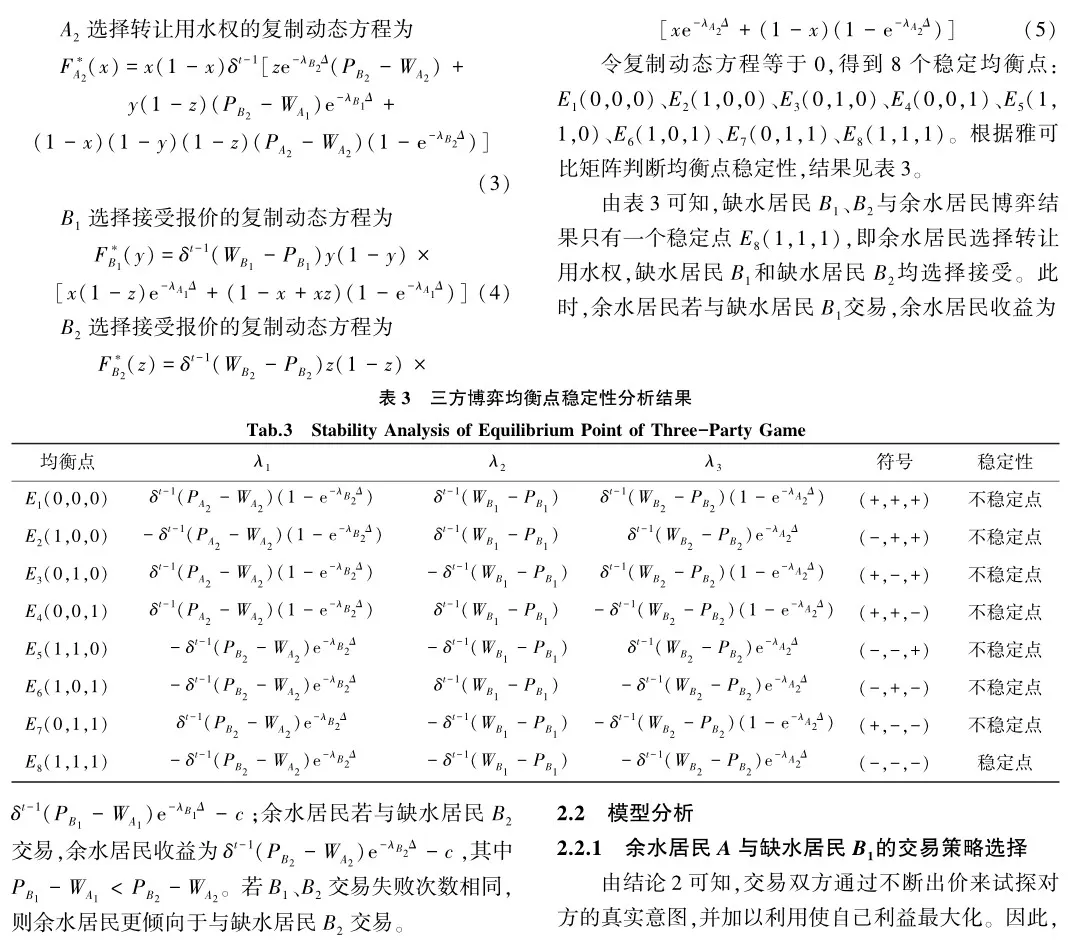
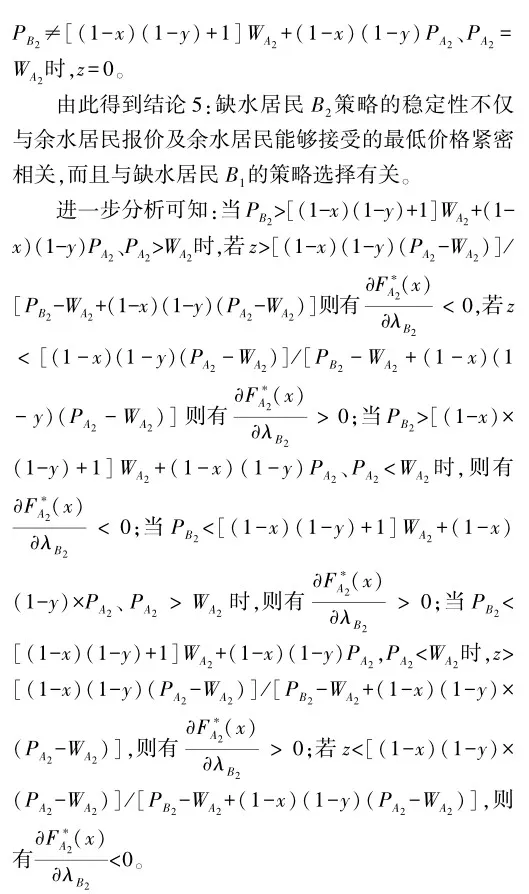
由此可得结论6：余水居民和缺水居民B2交易时的策略调整趋势与余水居民和缺水居民B1交易时的策略调整趋势相同。当缺水居民B2报价高于[（1-x）×（1-y）+1]WA2+（1-x）（1-y）PA2、余水居民报价高于其能接受的最低价格，且缺水居民B2接受余水居民报价的概率大于[（1-x）（1-y）（PA2-WA2）]/[PB2-WA2+（1-x）（1-y）（PA2-WA2）]时，余水居民根据缺水居民B2的态度调整自身策略的速度会变慢。

综上所述，当居民用水量未超过第二阶梯水量时，对于余水居民来说，不论是与缺水居民B1交易还是与缺水居民B2交易，如果缺水居民表达出购买用水权的意愿，余水居民则会更倾向于转让用水权，在日常生活中更倾向于节约用水来获得收益。对于缺水居民来说，当用水量超过第一阶梯水量时，缺水居民B1、B2均倾向于通过用水权交易购买用水权，而不是直接使用下一阶梯用水量。因此，市场需求会引导余水居民主动节水，使其拥有更多可交易的用水权，以此获得更大的经济收益。

3 数值仿真

3.1 交易价格分析

目前城市居民用水权交易尚未应用于实践，本文以黄河流域国家级中心城市郑州市为例，采用Matlab数值仿真软件来分析居民策略选择的变化趋势。根据《河南省城镇供水价格管理实施细则》及郑州市水费收费标准可知，郑州市第一阶梯水量为0～180m3，水价为4.4元/m3；第二阶梯水量为181～300m3，水价为5.95元/m3；第三阶梯水量为300m3以上，水价为10.6元/m3。考虑到数据合理性和仿真可操作性，假设余水居民能够接受的最低用水权交易价格为4.4元/m3，缺水居民B1能够接受的最高价格为5.95元/m3，缺水居民B2能够接受的最高价格为10.6元/m3。将假设的价格数值分别输入Matlab软件中进行数值仿真计算，并对仿真结果进行分析讨论。

3.1.1 情形1交易价格仿真

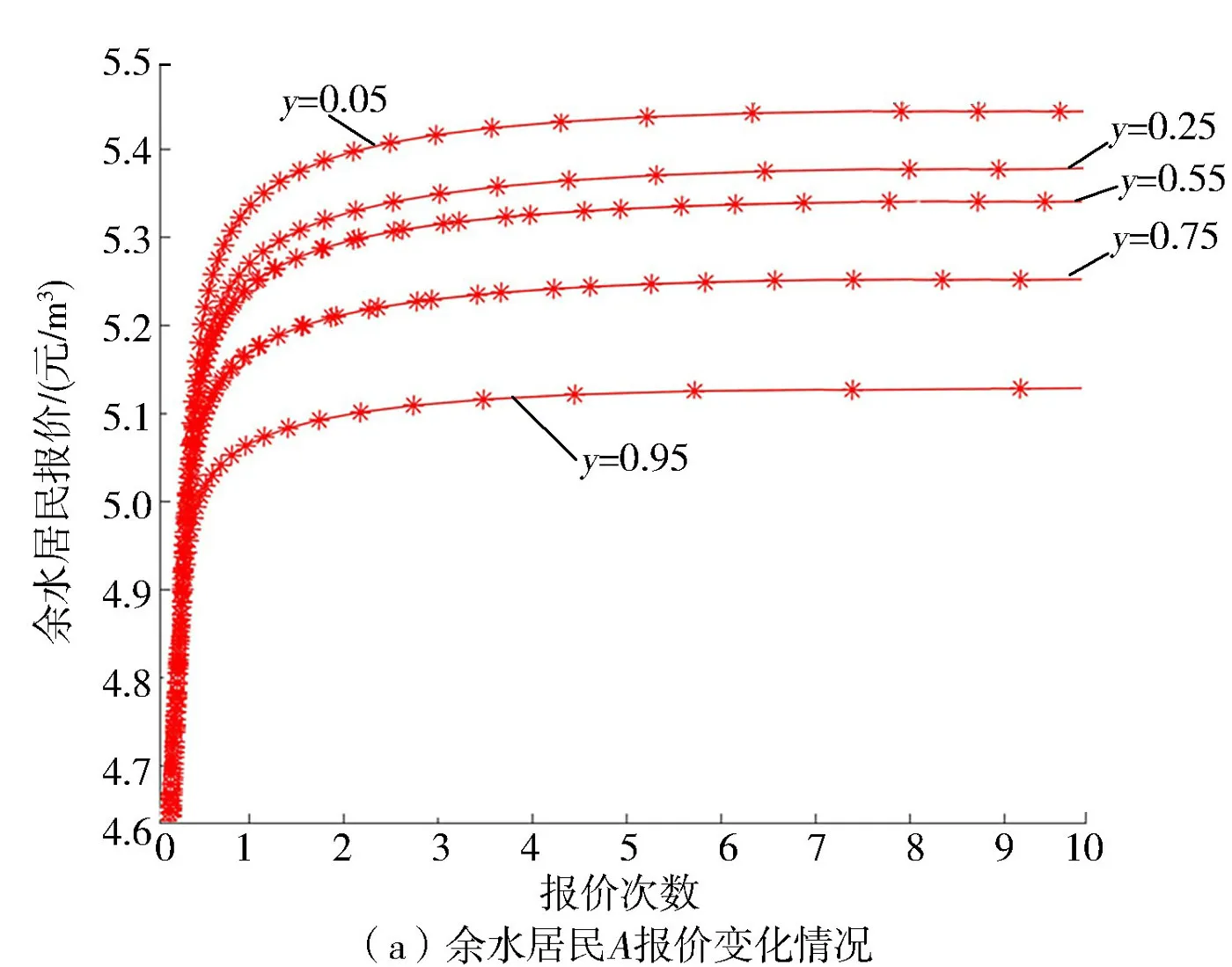
假设用水权交易双方的初始报价为（PA1，PB1）=（4.4，4.4）。由图1（a）可以看出，对于余水居民A而言，当缺水居民B1接受报价的概率增大时，余水居民A的报价逐渐降低。由图1（b）可知，对于缺水居民B1而言，其报价随着x增大而降低，当x在0.65附近时缺水居民B1的报价最低。

由图2可知，当x=0.15、y=0.25时，余水居民报价和缺水居民B1报价接近，最终报价均接近5.107元/m3；当x=0.30、y=0.45时，余水居民报价和缺水居民B1报价相近，最终报价分别为5.045元/m3和5.044元/m3。因此，通过仿真得到的用水权交易达成的两种情况为：余水居民转让用水权的概率为0.15，缺水居民B1接受报价的概率为0.25；余水居民转让用水权的概率为0.30，缺水居民B1接受报价的概率为0.45。当交易双方达成交易的概率增大时，其成交价格降低。

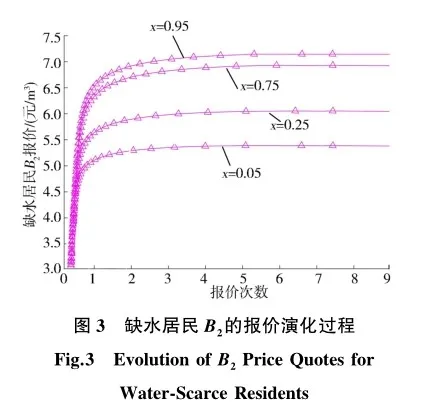
3.1.2 情形2交易价格仿真

假设交易双方的初始报价为（PA1，PB1，PB2）=（4.4，4.4，4.4）。由图3可以看出，缺水居民B2的报价随着余水居民转让用水权的概率增大而增大。与缺水居民B1的报价变化趋势对比发现，缺水居民B2的报价较高，余水居民与缺水居民B2交易得到的收益更大。因此，当缺水居民B1、B2均接受余水居民的报价时，余水居民会选择与缺水居民B2进行交易。

3.2 时间衰减因子δ对交易的影响

3.2.1 时间衰减因子δ对余水居民与缺水居民B1交易策略的影响

交易时间是影响用水权交易的重要因素。由上述分析可知，当余水居民报价为5.045元/m3、缺水居民B1报价为5.044元/m3时，两者实现水权交易的概率较高。将5.045和5.044输入Matlab软件中得到图4。可以看出，不论时间衰减因子如何变化，余水居民和缺水居民B1的策略最终均会向用水权交易达成的方向演化。当δ<0.35时，余水居民和缺水居民在交易前期策略演化速度较快；当δ>0.35时，余水居民和缺水居民在交易后期策略演化速度较快。

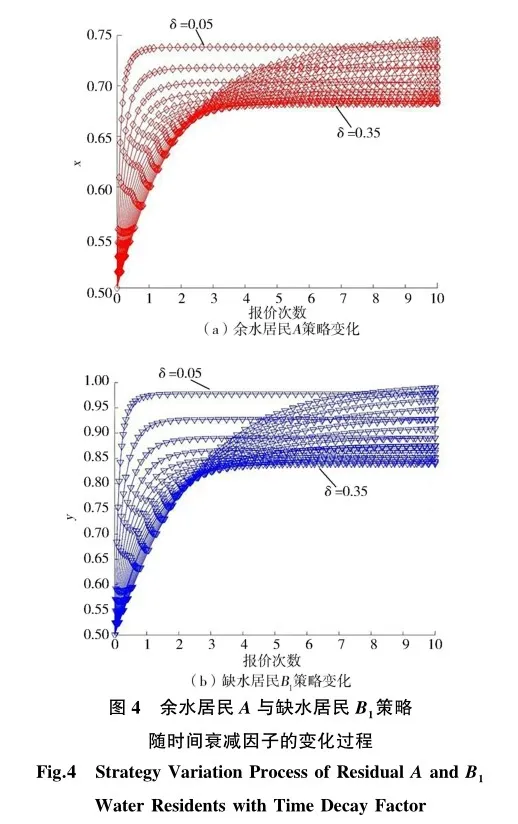
3.2.2 时间衰减因子δ对余水居民与缺水居民B2交易策略的影响

由图5可以看出，余水居民和缺水居民B2的策略均会向用水权交易达成的方向演化。δ值越大，缺水居民B2的策略演化速度就越慢，表明缺水居民B2在交易前期就有达成交易的意愿；当δ<0.35时在交易前期余水居民策略演化速度较快，当δ>0.35时在交易后期余水居民策略演化速度较快。

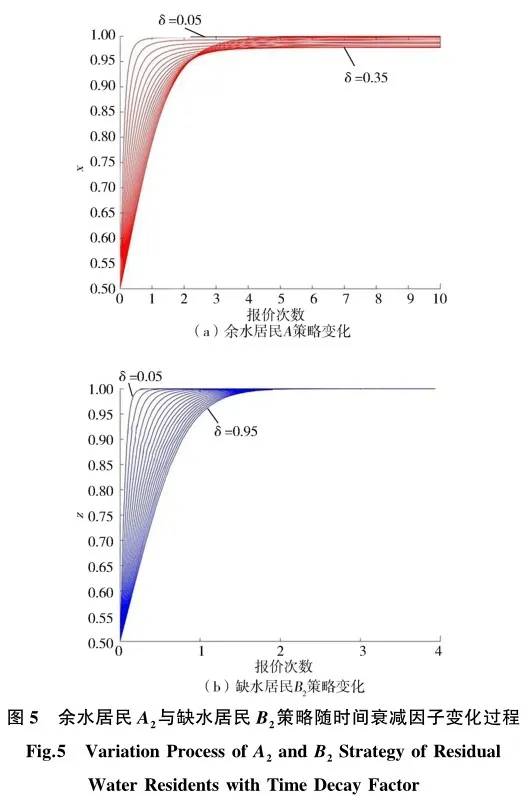
如果余水居民和缺水居民B1缺乏耐心，在交易前期会根据对方报价调整自己的策略以达成交易；反之，则在交易前期持观望态度并试探对方能接受的底线，在交易后期才会加快调整策略来达成用水权交易。

4 结论

本文利用演化博弈模型分析了不同主体参与城市居民用水权交易的两种情形，并以郑州市为例进行Matlab数值仿真，得到以下结论。

1）在用水权交易市场中，余水居民A和缺水居民B1、B2均可通过讨价还价达成用水权交易。缺水居民B2的报价高于缺水居民B1的，当缺水居民B2参与竞价时，余水居民A更倾向于与缺水居民B2进行交易。

2）在交易后期，余水居民A和缺水居民B1的策略变化速度随时间衰减因子的增大呈现先减小后增大的趋势。因此，余水居民A与缺水居民B1在交易前期持观望态度并试探对方能接受的底线，在后期更容易达成交易。

3）缺水居民B2的策略选择不仅与余水居民A有关，而且与缺水居民B1的策略选择有关。缺水居民B2的策略变化速度随时间衰减因子的增大而减小，因此余水居民A与缺水居民B2交易时应尽量缩短交易时间。

参考文献：

[1] 张保林.基于多主体系统理论的城市居民水权交易模型设计与仿真[J].价格月刊，2014（7）：80-85.

[2] SCHMACKM，ANDAM，DALLASS，etal.UrbanWater Trading？HybridWaterSystemsandNicheOpportunitiesinthe UrbanWaterMarket：ALiteratureReview[J].Environmental TechnologyReviews，2019，8（1）：65-81.

[3] GUANXJ，DUQY，ZHANGWG，etal.StudyonthePri？ cingofWaterRightsTransactionBetweenIrrigationWater UsersBasedonCooperativeGameinChina[J].Water，2021，13（12）：1672.

[4] SHENJQ，ZHUTT，SUNFH.AStudyontheMechanism andPricingofDrainageRightsTradingBasedonthe BilateralCallAuctionModelandWealthUtilityFunction[J].Water，2022，14（14）：2269.

[5] 田贵良，胡豪，景晓栋.基于演化博弈的水权交易双方行为策略选择及案例仿真[J].中国人口·资源与环境，2023，33（4）：184-195.

[6] 管新建，王宝勇，张文鸽，等.不同博弈情况下农户间水权交易价格研究[J].人民黄河，2022，44（10）：61-66.

[7] 张峰，程雪.中国工业用水需求价格弹性测算：基于联立方程模型[J].资源科学，2022，44（3）：583-594.

[8] 刘敏.“准市场”与区域水资源问题治理：内蒙古清水区水权转换的社会学分析[J].农业经济问题，2016，37（10）：41-50，111.

[9] 岳瑜素，王洁方，卢亚丽.黄河泥沙资源利用合作创新的演化博弈模型[J].人民黄河，2017，39（1）：21-23，29.

【责任编辑 张华兴】