基于模型集成的工程海量检测数据异常点识别方法

摘要：为提高公路工程中大量试验检测数据异常点的识别效率和准确性，提出采用“人工干预+检验模型”的异常点处理方法。通过基于领域+基于概率+基于线性+基于集成等4种类型算法对比后筛选初始模型，利用LSCP集成思路对初选模型进行集成运算，对检测数据集实现二次分类，提升模型检测的准确性和鲁棒性，对模型集成处理方法的有效性进行检验。结果表明，该模型能够使异常点识别查准率和灵敏度分别达到99.65%和96.99%，检测性能远高于其他单一算法。将该模型算法应用到云南某高速公路隧道涌水事故的监测数据检测，平均准确率为98.55%，表明该算法具有很好地异常检测效果。

关键词：公路工程；检测数据；模型集成；异常点识别；准确率

中图分类号：TP274文献标识码：A文章编号：1001-5922（2025）01-0157-04

A method for identifying outliers in massive engineering detection data based on model integration

DENG Aimin，NIE Liangpeng，LI Zhengyuan，XU Peng，FANG Shaobing

（Yunnan Tongqu Engineering Testing Co.，Ltd.，Kunming 650011，China）

Abstract：In order to improve the efficiency and accuracy of identifying outliers in a large amount of experimental detection data in highway engineering，an anomaly processing method“manual intervention+inspection model”was proposed.Through the comparison of four types of algorithms，including domain-based+probability-based+lin⁃ear-based+ensemble-based，the initial model was screened，and the LSCP ensemble idea was used to perform en⁃semble operation on the primary model，so as to realize the secondary classification of the detection dataset，improve the accuracy and robustness of model detection，and test the effectiveness of the model ensemble processing meth⁃od.The results showed that the model can achieve accuracy and sensitivity of outlier identification to 99.65%and 96.99%，respectively，and the detection performance is much higher than that of other single algorithms.The model algorithm was applied to the monitoring data detection of water inrush accident in a highway tunnel in Yunnan，and the average accuracy was 98.55%，indicating that the algorithm has a good anomaly detection effect.

Key words：highway engineering；detection data；model integration；identification of abnormal points；accuracy

在公路工程建设过程中，为确保工程质量和安全，需要进行大量的变形、位移、沉降、裂缝、强度、渗透等监测，在这些海量监测数据中，难免会存在一些异常点，这些异常点的存在往往可能会误导设计和施工参数的确定，危及工程建设质量和安全[1-3]。根据不同领域的需要，开发出了多种类型的异常值检测算法，如基于邻域的异常点检测算法[4]、基于概率的异常点检测算法[5]、基于线性的异常点检测算法[6]、基于集成的异常点检测算法[7]等。然而工程监测受天气等外力影响较大，在采用单一算法时，需要根据趋势变化对模型进行不断的训练调整，才能获得较高的识别精度，但这样会浪费大量的资源[8-9]。因此，研究提出“人工干预+检验模型”的异常点处理方法，将基于领域的异常点检测算法、基于概率的异常点检测算法、基于线性的异常点检测算法、基于集成的异常点检测算法等多种类型算法进行集成，从而提高异常值的检测精度，更好地为工程建设服务。

1算法简介

数据异常点检测算法根据原理可以划分为基于邻域的异常点检测算法、基于概率的异常点检测算法、基于线性的异常点检测算法、基于集成的异常点检测算法等多种类型。其中，基于领域的异常点检测算法核心思想为：异常点与内点分布存在差异，因此异常点所在的区域密度低或者与内点的距离很远，采用链接距离或者欧几里得距离来选择最近的邻居，从而实现异常点的检验，属于这类算法的有K最近邻算法（KNN）、局部异常因子算法（LOF）和基于连接的异常值因子算法（COF）等。基于概率的异常点检测算法核心思想为：假定数据样本服从某种概率模型，通过检查数据偏离样本均值的程度来检测数据集的异常点，为了应对不同大小数据集和不同维度数据集的使用需求，当前最常用的2种基于概率的异常检测算法分别为基于角度的离群点检测（ABOD）和基于copula函数的离群点检测算法（COPOD）。基于线性的异常点检测算法的核心思想是通过数据间映射关系来检测数据的异常值，常用的属于这一类算法的模型包括基于最小协方差行列式算法（MCD）和单类基于向量机的算法（OCSVM）。基于集成的异常点检测算法的核心思想是结合不同检测器或者是监测算法的检测结果重新生成更稳健的算法模型，然后减少某个模型对特定数据位置的依赖性，从而获得异常值，属于这类算法模型的有孤立森林算法（IForest）和并行异常值集合的局部选择性组合算法（LSCP）。

2模型集成检测算法构建过程

2.1初始模型选取

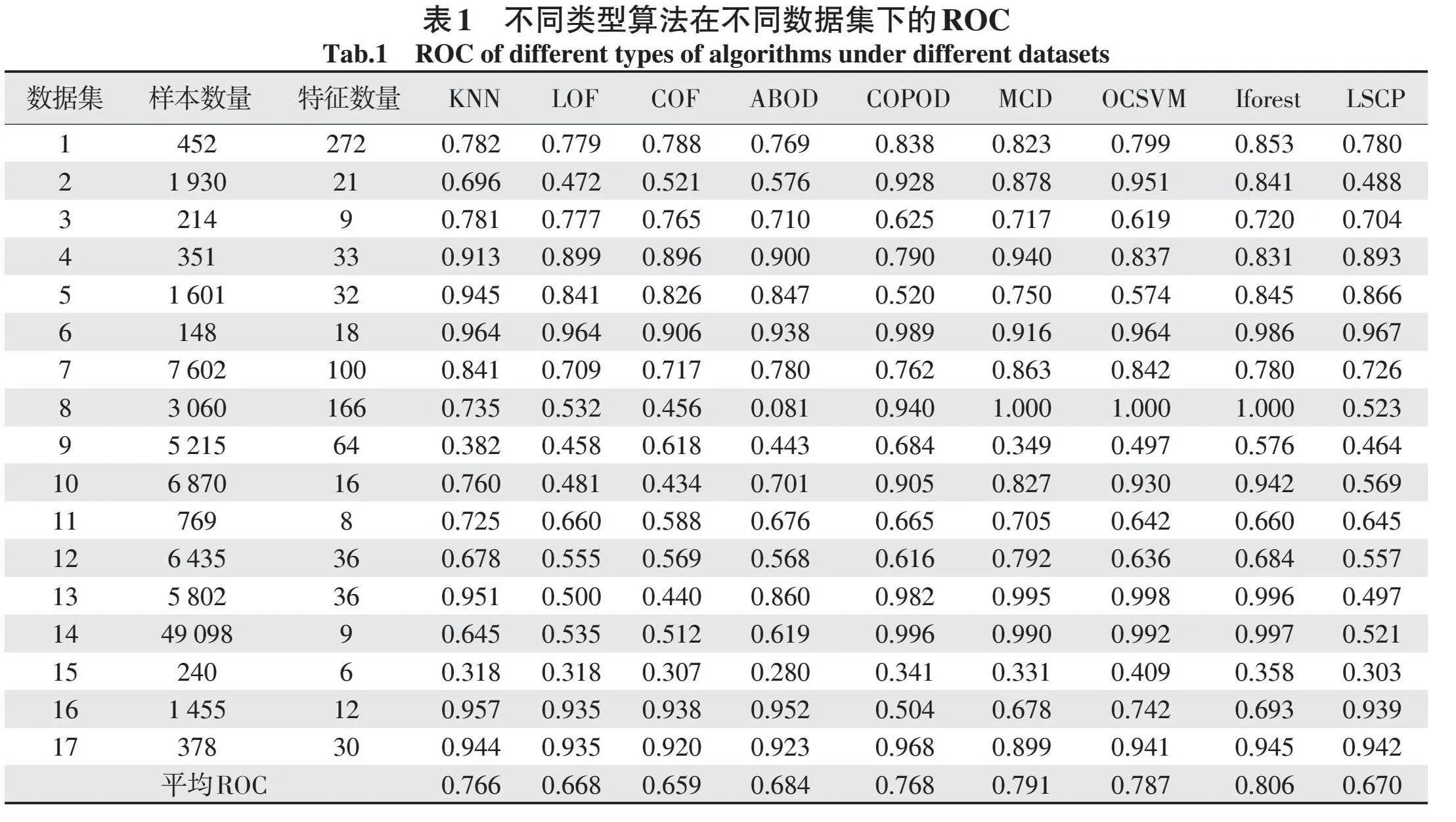
由于算法类型众多，模型集成不可能囊括所有算法，否则会造成模型集成计算量过大，影响异常点的检测效率，因此有必要在众多模型中选取最合适的算法来进行模型集成。随机选用UCI数据集中17组不同类型数据集，然后分别用不同算法对这17组数据集进行异常值检测，计算得到不同算法在17组数据集上的变动率（ROC）值，结果见表1。

由表1可知，9种算法模型在17种数据集下，均没有任何模型表现持续稳定，每种算法在某些数据下总有表现较差的现象，9种算法的平均ROC，按表现优劣排列依次为Iforest、MCD、OCSVM、COPOD、KNN、ABOD、LSCP、LOF、COF，Iforest算法检测稳定性最好。按同种类型算法检测效果对比，对于KNN、LOF和COF算法，KNN的检测效果最好，因此基于邻域异常点检测算法宜优先选择KNN算法；对于ABOD和COPOD算法而言，COPOD的检测稳定性更好，故基于概率的异常点检测算法宜优先选择COPOD算法；对于MCD和OCSVM算法，OC⁃SVM算法更加稳定，故基于线性的异常点检测算法宜优先选择OCSVM算法；对于Iforest和LSCP算法，Iforest算法表现更加稳定，故基于集成的异常点检测算法宜优先选择IForest算法。

2.2初分类

通过模型检测效果对比，筛选出了KNN、CO⁃POD、MCD和Iforest 4种算法进行模型集成训练，从而提高异常点的检测准确性。为检验初选模型的有效性，利用上述4种模型对UCI中的shuttle数据集进行异常点检测，该数据集包含正常数据点45 586个和异常数据点3 511个。

4种初选算法模型中，KNN模型相比其他3种模型，检测结果与实际结果最为接近，其他3种算法的检测结果相同，4种模型的检测结果均为有效。

2.3伪标签训练

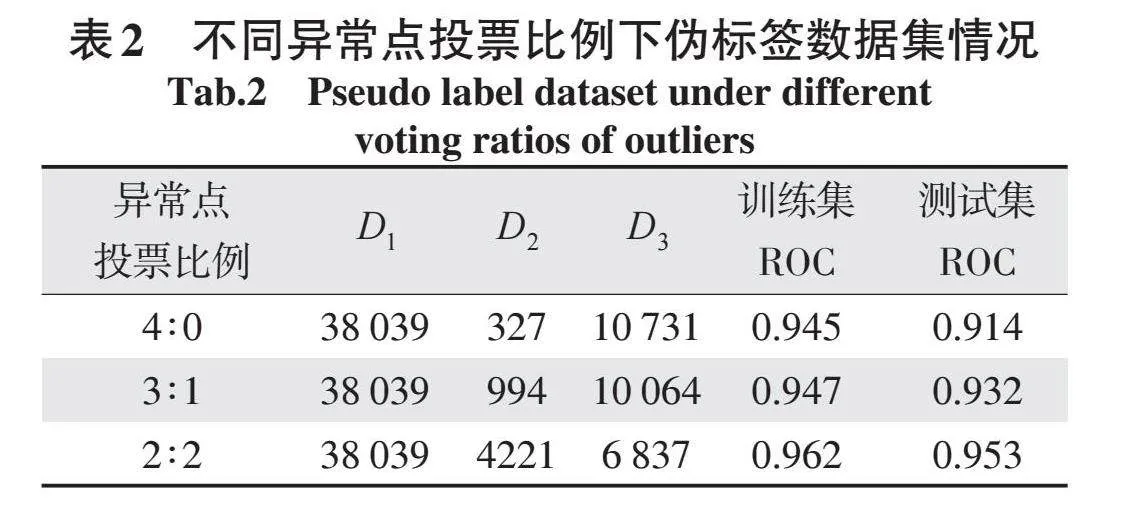
为了进一步提高检测的准确性，需要对上述4种分类结果进行整合。采用投票规则对4种模型的正常点和异常点进行投票，出现4∶0、3∶1和2∶2投票比例结果，由于工程检测数据的正常点远多于异常点，且正常点在后续工程建设中还需要进一步分析和利用，故在定义正常点时，需要比较严苛的标准，确保无监督条件下的检测尽可能准确。将4种模型检测结果均为正常点的点划分到正常点D1（即正常点投票比例为4∶0），而对异常点投票比例为4∶0、3∶1和2∶2投票结果的点进行二次划分，划分为异常点D2和人工规则之外的未被归类的中间点集D3，从而完成对工程检测数据集的二次划分，构造伪标签数据集。然后再根据伪标签数据集情况，将正常点和异常点按照6∶4的比例划分为训练集和测试集，并采用LSCP并行集成方式将KNN、CO⁃POD、MCD和Ifores这4种模型进行集成[10]，对不同异常点投票比例下的伪标签数据集进行异常检测，检测结果见表2。

2.4再分类

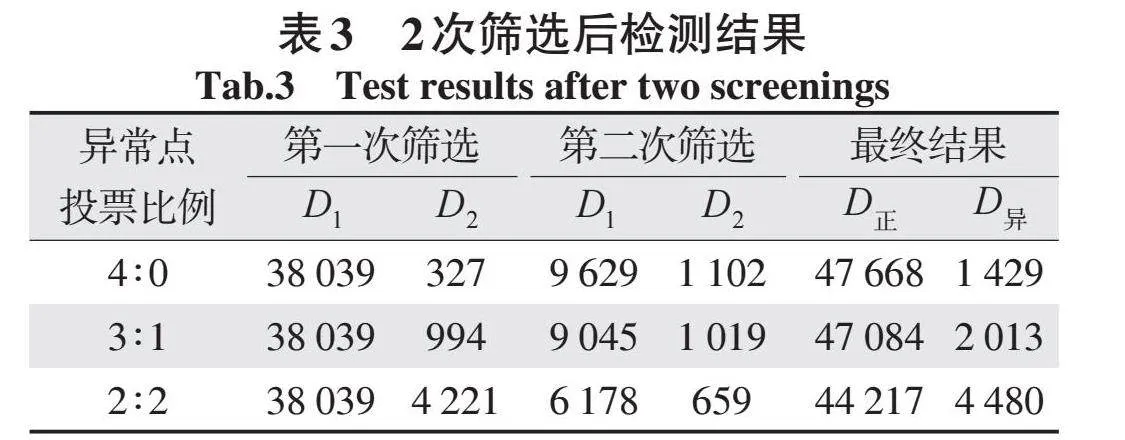
通过LSCP并行集成算法继续对中间点D3进行再次分类，分离出异常点和正常点，在人工干预情况下，经过2次筛选，最终得到正常点D正和异常点D异，见表3。

由表3可知，在不同投票比例下，当投票安排比例为2∶2时，D正和D异与实际情况最为接近，故模型集成投票比例选择为2∶2。

将所提模型集成检测效果与其他9种算法模型的检测效果进行对比，结果可知，无论从检测精确率还是检测灵敏度来讲，所提集成模型均较其他9种单一模型高，表明集成模型检测效果优异，在实际海量工程检测数据应用时，能够最大程度提高异常检测数据的准确，对于工程建设而言意义重大。

3模型集成算法应用

3.1案例背景

某高速公路工程全长42.76 km，桥隧占比达到42.7%，其中某特长隧道工程全长4.27 km，分为左右两线，设计形式为分离式小净距，隧道宽度为10.75 m，隧道高度为5 m，隧道设计高程为317.05～303.9 m，隧道顶部距地面最小距离为90 m。隧道穿越区主要地层岩性为粉质粘土、卵石、飘石等和残坡积层砂质粘土，下伏基岩岩性主要以片麻岩和石英岩为主，岩体分布全风化、强风化、中风化和微风化，地下水埋藏较浅，地下水丰富。隧道周边大部分民房为土坯房和简易砖混房，年久失修，多数存在不同程度的原生裂缝，且居民生活、生产用水以周边地表和溪流水为主。

隧道右线开挖至DK2+838掌子面时，出现大量渗水涌水，涌水口直径从0.15 m注浆扩大至0.8 m，涌水量1 000～1 300 m3/h。在涌水发生过程中，引发了隧道周边地层发生沉降塌陷、房屋开裂、地表水干涸以及农田损坏等多种次生灾害。根据现场地勘情况，确认了本次涌水潜在影响区为掌子面前方即左右两侧约100～800 m；在现场总共划出了A、B、C 3个监测区，在3个监测区内共布置了23个监测点，监测参数包括地表变形、地基沉降、裂缝和水位，监测期间共获得10 949个地表变形、10 008个地基沉降、3 347个裂缝和1 317个水位监测样本数据。

3.2异常检测过程

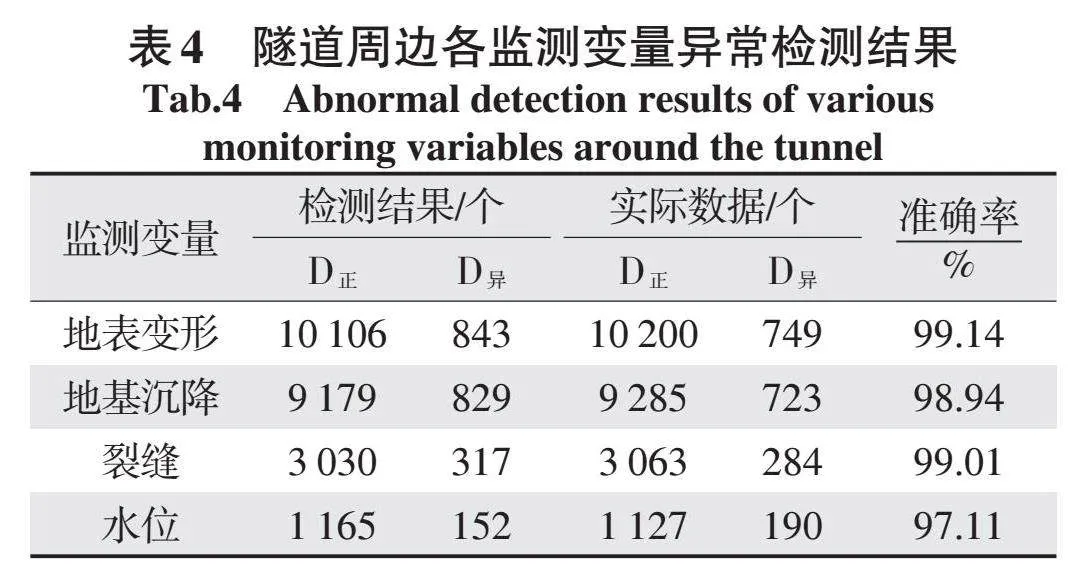
首先，分别利用KNN、COPOD、MCD和Iforest 4种算法对4种监测样本数据集进行异常检测，然后按照正常点投票比例4∶0，异常点投票比例2∶2的筛选规则对数据集进行初次划分；然后将数据集划分为正常点集D1、异常点集D2和中间点集D3，得到伪标签数据集，接着再通过LSCP并行集成框架将4种模型进行集成；然后，将所有中间点集D3再次进行划分，最后将2次划分得到的正常点和异常点数量相加，得到最终的检测结果，见表4。

由表4可知，采用集成模型检测得到的地表变形正常点和异常点分别为10 106个和843个，异常点占比为7.7%；地基变形正常点和异常点分别为9 179个和829个，异常占比为8.3%；裂缝正常点和异常点分别为3 030个和317个，异常点占比为9.5%；水位正常点和异常点分别为1 165个和152个，异常点占比为11.5%。将检测结果与实际结果进行对比，地表变形、地基沉降、裂缝和水位的检测准确率分别为99.14%、98.94%、99.01%和97.11%，平均准确率为98.55%。可见，本文提出的集成模型能够很好地完成海量工程检测数据的异常检测工作。

4结语

（1）利用9种不同类型算法对UCI中随机17种数据集进行检测，得到9种算法的ROC值排序为If⁃orest、MCD、OCSVM、COPOD、KNN、ABOD、LSCP、LOF、COF，分别选取基于邻域KNN、基于概率CO⁃POD、基于线性MCD和基于集成Iforest算法来构建集成模型；

（2）利用筛选出的4种算法模型首先对数据集进行初分类，再通过LSCP并行集成方式对模型进行集成和二次分类，将二次分类得到的数据点相加，获得最终检测分类结果，结果表明本文提出的基于集成模型的异常点检测查准率和灵敏度均高于其他单一算法模型，具有较高的异常点检测潜力；

（3）将集成模型应用到某高速公路隧道工程涌水事件监测的异常检测中，异常值平均检测正确率达到98.55%，检测效果优异。

【参考文献】

[1]王晨阳，张子新，黄昕，等.地下工程多时间序列监测数据异常检测算法[J].现代隧道技术，2022，59（S1）：171-179.

[2]郭松，尹晓星，李福平，等.基坑沉降监测小样本数据非等间距灰色建模与应用[J].工程勘察，2022，50（3）：67-71.

[3]尤辰汀.基于数据特征分析的污染源监测数据异常值识别方法研究[J].环境科学与管理，2023，48（2）：133-138.

[4]刘意，毛莺池，程杨堃，等.基于邻域一致性的异常检测序列集成方法[J].计算机科学，2022，49（1）：146-152.

[5]郭鹏.基于概率的网络异常数据流的检测方法[J].新乡学院学报，2021，38（6）：43-46.

[6]徐胜超，宋娟，潘欢.基于线性回归与最小二乘法的物理主机状态异常检测方法[J].计算机与现代化，2021（5）：105-111.

[7]庄锐，张浩.基于平均特征重要性和集成学习的异常检测[J].计算机系统应用，2023，32（6）：60-69.

[8]杨碎明，曹雅蓉.基于集成分类器的网络异常流量特征选择模型[J].自动化技术与应用，2022，41（4）：34-37.

[9]邝萌，李英娜，李川，等.基于多模型融合Stacking集成学习的异常用电检测方法研究[J].电力科学与工程，2021，37（3）：23-29.

[10]陈江雨，李培强，钟吴君.基于多模型并行集成框架的风电功率异常数据识别[J].电力系统及其自动化学报，2023，35（11）133-142.

（责任编辑：平海，苏幔）