中考中的“几何图形初步”

“几何图形初步”中的有关知识是学习初中几何的基础，也是中考命题的重点素材．

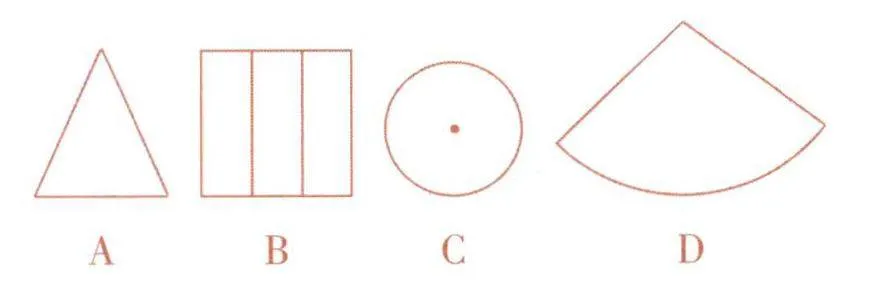
例1 （2024年甘肃）如图1所示，从前面看该几何体得到的平面图形是（ ）．

解析：根据从前面看的要求，得到的是选项C中的平面图形，故选C．

点评：解决从不同方向看得到的平面图形问题，要抓住两点：第一，弄清观察的方向：第二，掌握观察的方法．

例2 （2024年青海）生活中常见的交通锥通常是圆锥的形状（如图2），它的侧面展开图是（ ）．

解析：根据圆锥的侧面展开图是扇形，可知应选D．

点评：确定简单几何体的侧面展开图的关键是熟悉常见几何体的侧面展开图．

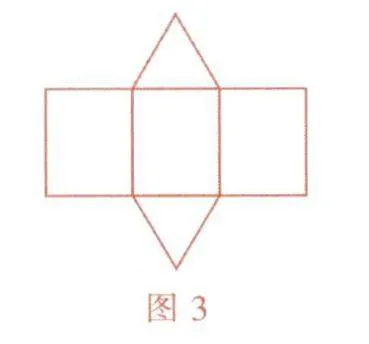
例3 （2024年扬州）图3是某几何体的表面展开后得到的平面图形，该几何体是（ ）．

A．三棱锥

B。圆锥

C．三棱柱

D．长方体

解析：由图3可知，这个几何体的展开图的底面为三角形，侧面为长方形，可知该几何体是三棱柱，故选C．

点评：本题考查由展开图得到对应的立体图形．解决这类问题的关键是熟记常见立体图形的展开图特征．

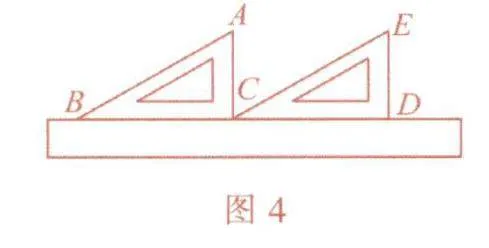
例4 （2024年广东）如图4，把一把直尺和两个含30，角的三角尺拼接在一起，则∠ACE的大小为（ ）．

A.120°

B.90°

C.60°

D.30°

解析：由题意可知∠ACB=90°，∠DCE=30du3，而真∠ACB+∠ACE+∠DCE=180°，故∠ACE=180°-90°-30°=60°，应选C．

点评：解决此类问题的关键是熟知三角尺的各个角的大小，想一想：利用这两个三角尺，还可得到怎样的问题？若换成两个含45°角的三角尺，又会得到怎样的问题？