深入理解概念 通盘考虑问题

在学习“几何图形初步”时，我们一不留神就容易出错．万老师为大家收集了一些常见错解，希望同学们能以错纠错，以防再错，为今后进一步学习更复杂的几何图形及其性质作好准备．

一、观察不细

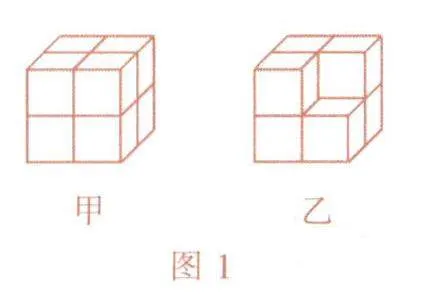
例1 图1中，甲（由8个边长为1的小正方体组成）的表面积（ ）乙（由7个边长为1的小正方体组成）的表面积．

A．大于

B．小于

C．等于

D．不能确定

错解：选A．

剖析：从图形上看，乙比甲少了1个小正方体，有些同学误认为表面积肯定也会减少，立体图形的表面积是指立体图形所有外表面的面积之和.由题意可知甲的表面积为4×6=24，乙的表面积为4×3+3×3+3×1=24，两个立体图形的表面积相等．

正解：选C．

二、表达不清

例2 某同学用剪刀沿直线将一片平整的树叶剪掉一部分（如图2），发现剩下树叶的周长比原树叶的周长要小．能正确解释这一现象的数学知识是（ ）．

A．两点之间，线段最短

B．两点确定一条直线

C．经过一点有无数条直线

D．直线比曲线短

错解：选B或D．

剖析：选B的同学看到“沿直线”，联想到两点确定一条直线，而没有考虑到题意是比较两点之间曲线与线段的长短：选D的同学没有真正理解题意．

正解：选A．

三、推理不明

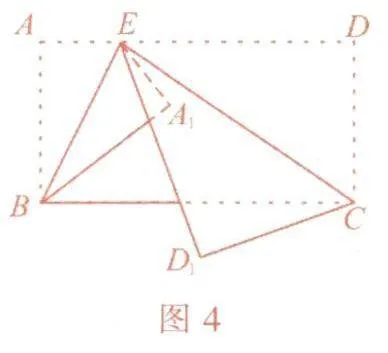
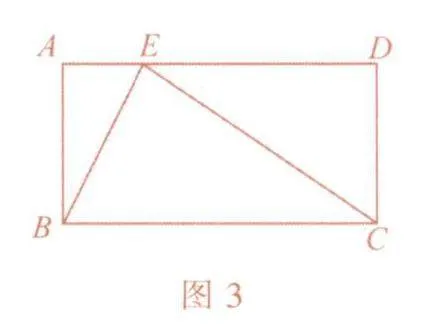
例3 如图3，在长方形ABCD中，点E在AD上，并且∠BEA =64°．分别以BE，CE为折痕进行折叠并压平，如图4．若图4中∠A1ED1=18°，则∠DEC的大小为______．

错解：填“26°”

剖析：有些同学误认为∠BEC等于90°，在求∠DEC的大小时利用180° -90°-64°得26°.

事实上，由题意得∠AEA1=2∠BEA=128°.因为∠A1ED1=18°，所以∠AED1=∠AEA1-∠A1ED1=110°，故∠DED1=180°-∠AED1=70°．

由题意得∠DEC=∠D1EC=1/2∠DED1=35°.