与数轴有关的问题

对教材上的习题进行反思，能让我们受益匪浅．

例1 （人教版数学教科书七年级上册第168页第7题）A，B，C是数轴上的三个点，点A表示数3，且线段AB的长为4，C为线段AB的中点，点C表示的数是多少？

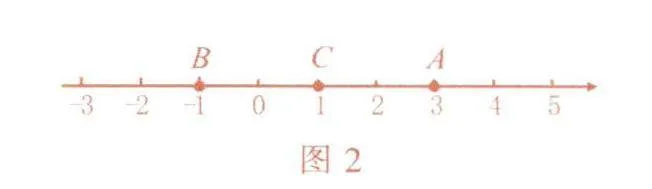
解析：当点B在点A的右侧时，如图1．因为点A表示数3，线段AB的长为4．所以点B表示数7．因为C为线段AB的中点，所以A C=BC.设点C表示数x，则x-3 =7-x．解得x=5.

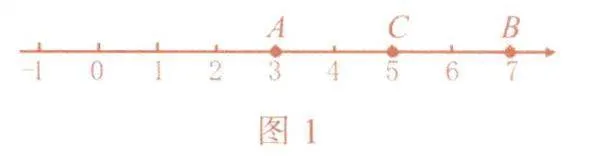
当点B在点A的左侧时，如图2．因为点A表示数3，线段AB的长为4，所以点B表示数-1.因为C为线段AB的中点，所以BC=CA．设点C表示数x，则x-（-1）=3 -x，解得x=1.综上所述，点C表示的数是5或1．

反思1：观察图1，点A表示数3，点B表示数为7，AB=7-3=4或者A B=-（3-7）=4；观察图2，点A表示数3，点B表示数-1．AB=3-（-1）=4或者A B=-（ -1 -3） =4.由此可知，若点A表示数x1，点B表示数x2，x1＜x2，那么AB=x2-x1或者AB=-（x1 -x2），综合得AB=|x1-x2|．于是我们得到数轴上求两点间距离的一个公式：在数轴上，如果点A表示数x1，点B表示数x2，那么，AB=|x1-x2|.

反思2：图1中，点A表示数3，点B表示数7，点C表示的数是5，注意到3+7/2=5；图2中，点A表示数3，点B表示数-1，点C表示的数是1，注意到3+（-1）/2=1．

由此可知，在数轴上，如果点A表示数x1，点B表示数x2，那么AB的中点c表示数x1+x2/2．

回到例1，此时，若设点C表示的数为x0，点B表示的数为x，因为C为线段AB的中点，所以BC=CA，则3-x/2=x0，解得x=2x0-3．因为AB=4，所以|（2x0-3）-3|=4，所以2x0-6=±4，故可得x0=5或x0=1．

受此启发，还可这样解：设点C表示的数是x0，因为C为线段AB的中点，所以CA=1/2AB=2，所以|x0-3|=2，所以x0-3=±2，故可得x0=5或x0=1．

试一试

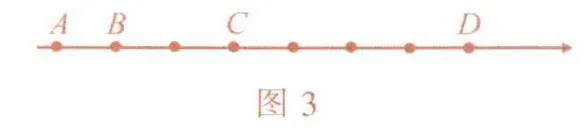
如图3，在数轴（不完整）上标出若干个点，每相邻两点相距一个单位长度，点A，B，C，D分别表示整数a，b，c，d，且d=3c，则原点在（ ）的位置．

A．点A B．点B

C．点C D．点D

参考答案：B