积淀操作经验 发展想象能力

在日常生活中，千姿百态的图形美化了我们的现实世界，这些图形既赋予了我们美的体验，又为我们提供了诸多便利。同时也启发我们去思考：图形世界有哪些秘密？精美的物品都是由哪些基本图形构成的呢？

一、图形的由来

相传四千年前，古埃及尼罗河每年都会洪水泛滥，泛滥的洪水在带来肥沃淤泥的同时，也模糊了原有的土地界线．为了应对尼罗河洪水过后的土地界线问题，尼罗河流域的人们每年都会进行土地测量，因而，古埃及人积累了许多土地测量知识，也为几何学的早期发展奠定了基础．

我国对几何学的研究历史同样悠久，我国新石器时代的黑陶器皿上的花纹演变逐渐由鱼形过渡到不规则图形，再到菱形、正方形等规则几何图形；墨翟及其弟子所著《墨经》里也有几何图形的相关知识；成书不晚于公元前2世纪的中国数学典籍《周髀算经》里记载了直角三角形三边之间的关系；成书最迟在公元前1世纪的中国古代数学典籍《九章算术》里详细记载了土地面积和物体体积的计算方法，此外，我国古代数学家祖冲之、刘徽等对几何学的发展都做出了重大贡献．

几何图形并不是数学家凭空创造的产物，而是由现实世界的实物抽象和提炼而来的．在现实世界中，存在着各种各样的几何图形，包括简单的几何图形，以及由简单几何图形组成的复杂几何图形．

一些几何图形（如线段、角、三角形、长方形、圆等）的各部分都位于同一个平面内，它们是平面图形，而有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一个平面内，它们是立体图形．

二、图形的应用

几何图形的应用十分广泛，尤其在创意文化用品和家居用品领域，几何图形扮演着重要角色，几何图形在帮我们解决生活问题的同时也美化了生活环境，现在我们提出一个问题：

能否利用手中的材料，制作一个正五棱柱呢？

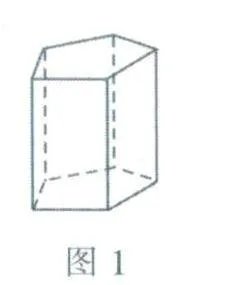
观察正五棱柱（如图1所示），可以发现正五棱柱的上表面和下表面是一样的正五边形．侧面都是矩形，并且这些矩形都具有特定的性质：宽与正五边形的边长相等，长全部都相等，正五棱柱的展开图需要满足这样的条件：上表面和下表面至少要有一条边与侧面连接，而侧面之间则不必完全连接．

下面我们开始动手做．

（1）制作正五棱柱的展开图，正五棱柱的展开图大致分为两类：

当侧面都连在一起时，只要两个一样的正五边形在侧面所连成的大矩形的两侧即可（如图2所示）.

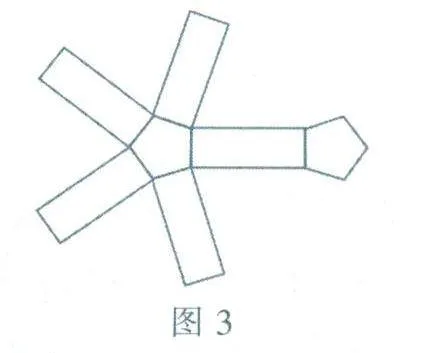
当侧面和侧面不连接在一起时，有一个正五边形就会和每一个侧面都相连，另一个正五边形和其中的一个侧面相连即可（如图3所示）．

这两类展开图均可组成一个正五棱柱．

（2）任选第一步中可以组成正五棱柱的一个展开图，将展开图折叠起来，用胶粘好，一个正五棱柱就做好了．

三、图形的学习

和数与代数、统计与概率领域的学习相比，几何图形领域的学习更需要在直观操作和思考推理中完成．

1．动手实践．

在本章中，教科书精心设计了丰富的数学实践活动，许多数学结论和图形的性质不是直接呈现给我们的，而是要求我们亲自动手操作和探索，通过亲身体验，进而理解和掌握数学结论及图形的性质．

2．细致观察．

在几何图形的学习中，同学们需要学会如何从不同角度观察和分析问题．在解决现实世界中的问题时，这是非常重要的技能．例如，在规划一个花园时，同学们需要考虑如何最有效地利用空间，解决这样的实际问题不仅使学习变得有意义，而且能帮助同学们认识到数学的重要性和实用价值．

3．激发想象．

数学学习离不开丰富的想象，尤其是几何图形的学习，更离不开想象，虽然本章提供了大量动手操作的数学活动，但是，我们不能完全依靠动手操作去探究所有的数学结论．

事实上，先想象一下，然后动手操作，再回想操作过程，是培养我们想象能力的重要环节．

4．学思结合．

“学而不思则罔”，在数学学习中，我们不能仅仅满足于动手操作的活动层面，应该在操作的每个环节以及操作结束后进行深入思考：我是怎么进行操作的？为什么要这么做？这样的操作方法是否有效？接下来我应该采取什么步骤？这个活动涉及哪些数学知识？通过这个活动我学到了什么？

总之，在“几何图形初步”学习中，多一次动手、多一分观察、多一次想象、多一分思考，就会多一点收获！

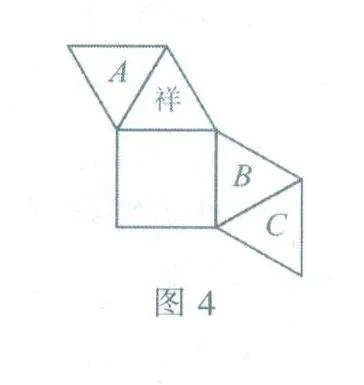
（2024年德阳）走马灯，又称仙音烛．史料记载，走马灯起源于隋唐时期，盛行于宋代，是中国特色工艺品，常见于除夕、元宵、中秋等节日，在一次综合实践活动中，一位同学用如图4所示的纸片，沿折痕折合成一个棱锥形的“走马灯”，正方形做底，侧面有一个三角形面上写了“祥”字，当灯旋转时，正好看到“吉祥如意”的字样，则在A，B，C处依次写上的字可以是（ ）．

A．吉、如、意

B．意、吉、如

C．吉、意、如

D．意、如、吉

参考答案：A