基于灰色理论的广东省人口老龄化趋势预测及影响因素

摘" "要：中国人口老龄化现象持续加剧，对经济运行全领域、社会建设各环节、社会文化多方面乃至国家综合实力和国际竞争力都具有深远影响。因此，将广东省人口老龄化作为研究对象，基于GM（1，1）模型，探究2022—2035年老年人口数量及其占比的变化趋势。再运用灰色关联分析和主成分分析方法，分析影响老龄化的8个因素，找出主要影响因素。结果表明：未来14年65岁及以上老年人口数量及其占比将呈现逐年递增趋势，预计到2035年，65岁及以上老年人口数量将达到1 584.735 2万人，占比将达到9.971543035%；城镇化率、死亡率、出生率、卫生技术人员数、医疗卫生机构床位数和人均GDP是影响老龄化的六个重要因素；经济发展因素和人口结构因素是影响老龄化的两个主要成分。

关键词：人口老龄化；GM（1，1）模型；灰色关联分析；主成分分析；影响因素

中图分类号：C921" " " " 文献标志码：A" " " 文章编号：1673-291X（2024）22-0067-06

近年来，我国人口老龄化问题日益突出，未来老龄化现象仍将持续加剧。这一问题对于经济建设、政治建设、文化建设、社会建设、生态文明建设等多方面乃至国家综合实力和国际竞争力都具有相当深远的影响。特别是处于我国改革开放前沿阵地的广东省，理清其人口老龄化发展趋势及影响因素更具重要意义。根据广东省统计年鉴，截至2021年年末，全省常住人口为12 684万人，位居全国首位。65岁及以上老年人口为1 615万人，占12.73%。广东省已成为全国老年人口最多的10个省份之一，并且65岁及以上老年人口数量逐年递增，老龄化速度正在不断加快。通过对广东省人口老龄化的研究，为我国应对人口老龄化问题制定相关的人口政策，同时提出相应的应对方案。

国内外已有不少学者对人口老龄化问题进行了研究。在人口老龄化对经济和社会的影响方面，David和Bloom等[1]认为，生育率的下降将导致劳动年龄人口的比率上升，而劳动年龄人口的增加将减小人口老龄化发展对经济的影响，因此人口老龄化不会对发展中国家的经济发展有明显阻碍。Dall和Timothy[2]在美国人口老龄化的背景下，预测了未来对医疗保健服务的需求。在人口老龄化的预测方面，韩鹏和宋晓晓[3]利用GM（1，1）模型对内蒙古老年人口进行了预测。杨华[4]构建了NSGA-III-WFGO-GM（1，N）与BP神经网络的组合模型并应用于人口老龄化预测。胥俊林和陈友军[5]利用新陈代谢灰色模型预测了人口老龄化。在人口老龄化的影响因素方面，大多数研究者认为，出生率和死亡率的降低是导致人口老龄化的主要原因，例如Walford和Kurek[6]对英国和波兰的人口老龄化进行对比后发现，这两个国家的人口老龄化都是由出生率和死亡率的降低导致的。田甜[7]以中国西部地区为研究对象，运用空间自相关和地理探测器等方法进行研究，得出人口老龄化空间分布特征的主要影响因子是人口自然增长率、职工平均工资。胡琼和罗娟[8]利用上海市2007—2018年统计年鉴数据，运用灰色关联理论分析了上海市人口老龄化的主要影响因素，发现GDP增长率、人均可支配收入、卫生服务人员数与出生率等对其影响较大。陈宁[9]采用年龄移算和队列要素分析等方法预测“全面二孩”政策对人口老龄化的发展速度有一定抑制作用，有助于降低老年抚养比，降低劳动力供养负担。

从现有研究成果来看，不同角度、不同方法的研究都有助于揭示人口老龄化的发展趋势及影响因素。鉴于此，文章尝试对于老龄化人口数量建立GM（1，1）模型[10]，并进行研究、分析和预测。再进行灰色关联分析和主成分分析，分析影响老年人口数量及其占比的8个因素，得到影响人口老龄化的主要因子。

一、人口老龄化的趋势预测

（一）数据选取

数据主要来源于《广东省统计年鉴》（2001—2022）、《国家统计年鉴》（2001—2022）、广东省第七次人口普查公报（第四号）、第七次人口全国普查公报（第五号）、国家统计局数据库。

（二）GM（1，1）模型

GM（1，1）模型是一种对含有不确定因素的系统进行预测的模型。建模过程中所需信息较少，运算简便，精度较高，易于检验，也不必过分关注数据的分布规律或检验特征。本质是通过微分方程来充分挖掘数据的内在规律，预测数据未来的发展趋势，特别能对数量较少、完整性和可靠性较低的数据序列进行有效的预测。具体来说，首先，需要进行关联分析，就是鉴别系统各种因素之间发展趋势的相异程度。因为这些因素的影响会使得表现系统行为特征的数据显得无规律，但其实这些看似无规律的数据也有可能是潜在的有规律数据的一种表现。其次，通过累加或累减的方式对原始数据进行处理，以便得到有较强规律性的数据，进而寻找内在的规律性。最后，建立相应的微分方程模型，预测数据未来的发展趋势。

（三）数据预处理

1.级比检验

为了弱化数据的随机性，对65岁及以上老年人口数量记为X（0），并对X（0）进行级比检验。记X（0）={X（0）（1），X（0）（2），...，X（0）（n）}，令λ（k）=X（0）（k-1）/X（0）（k）（k=2，3，...，n），经过计算可知并非所有的λ（k）均落入区间（e-2/（n+1），e2/（n+1））之内。因此，对X（0）作平移变换，即对X（0）的每个值都加上常数C，再进行检验。当C=668时，X（0）通过检验，说明X（0）可使用GM（1，1）模型进行分析。对65岁及以上老年人口占比也进行级比检验，当C=7时，数据通过检验，说明也可使用GM（1，1）模型进行分析。

2.数据累加

对X（0）进行累加。令X（1）（K）=" X（0）（i）=X（1）（k-1）+X（0）（k）（k=1，2，...，n），则生成数据为X（1）={X（1）（1），X（1）（2），...，X（1）（n）}。对于非负数据，累加次数越多，随机弱化越强。当累加次数足够多时，可认为X（0）已由随机序列变为非随机序列了。一般经过多次累加后，多数序列可用指数曲线进行逼近。

（四）模型建立

定义X（1）的灰导数为d（k）=X（0）（k）=X（1）（k）-X（1）（k-1），令Z（1）为X（1）的均值序列，且Z（1）（k）=0.5X（1）（k）+0.5X（1）（k-1）（k=2，3，...，n），则Z（1）=（Z（1）（2），Z（1）（3），

...，Z（1）（n））。此时灰微分方程模型为d（k）+az（1）（k）=b，即X（0）（k）+az（1）（k）=b，其中X（0）（k）为灰导数，a为发展系数，z（1）（k）为白化背景值，b为灰作用量。

令u=（a，b）T，Yn=（X（0）（2），X（0）（3），...，X（0）（n）），B=-Z （2）" -Z （3）" ..." "-Z （n）" " "1" " " " " " " 1" " " "..." " " " 1 ，则由最小二乘法，求使 J（u）=（Yn-Bu）T（Yn-Bu）达到最小值的u=（a，b）T=（BTB）-1BTYn。解微分方程，即可得到预测值

对65岁及以上老年人口数量建立GM（1，1）模型，所得结果为：

对65岁及以上老年人口占比也建立GM（1，1）模型，所得结果为：

（五）模型检验

采用拟合图法、后验差检验法和小误差概率检验法分别对模型（1）和（2）进行检验。

1.拟合图法

将模型（1）的真实值与预测值做成拟合图进行分析（见图1），可以看出模型的拟合效果较好，预测结果理想。

将模型（2）的真实值与预测值做成拟合图进行分析（见图2），可以看出模型拟合出了真实值的趋势，预测结果较为理想。

2.后验差检验法和小误差概率检验法

对于模型（1），先计算原始序列的标准差S1= （X （k）-X ） /（n-1），再计算误差序列的标准差S2= （ε （k）-ε ） /（n-1），两者相除得到方差比率C=S2/S1=0.237，最后计算小误差概率P=P（|ε （k）-ε |lt;0.6745S1）=1.0。根据GM（1，1）模型拟合精度等级标准（见表1），确定模型（1）的精度等级为好，检验通过。同理，可算出模型（2）的方差比率C=0.624，小误差概率P=0.818，确定模型（2）的精度等级为基本合格，检验通过。

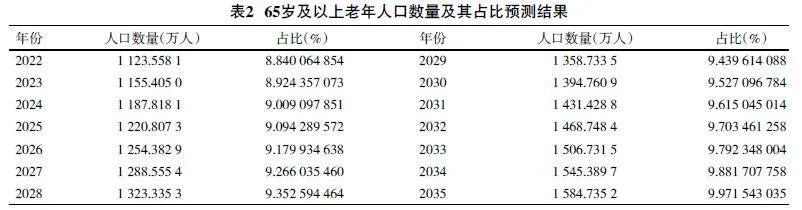
口增长速度加快，且在未来14年65岁及以上老年人口数量还将持续增长。预计到2035年，65岁及以上老年人口数量将达到1 584.735 2万人，占比将达到9.971543035%。老年人口规模不断扩大，老年化现象逐渐严重，老年人的赡养负担逐渐加重，将会持续增大年轻人的社会压力，这些都将对经济和民生等造成一定的影响。

二、人口老龄化的影响因素

（一）数据选取

筛选出X1人均GDP（万元）、X2出生率（%）、X3死亡率（%）、X4城镇化率（%）、X5卫生技术人员数（万人）、X6医疗卫生机构床位数（万张）、X7基本养老保险支出（亿元）、X8基本医疗保险支出（亿元）共8个主要影响因素。

（二）数据预处理

在收集数据的过程中，因为某些统计指标在早年没有数据记载，再加上其他因素的影响，不可避免地使某些统计指标在部分年份出现了缺失值，所以要对数据进行预处理，即进行数据的填充。根据插值法的思想用最可能的值来插补缺失值，大量的研究表明这要比删除不完全样本或变量丢失的信息少[11]。因此，选择用Excel软件来绘图观察之后插入缺失值。

（三）灰色关联分析

灰色关联分析是对系统发展变化的趋势提供量化的度量，十分适合动态历程分析。主要步骤为：

第一步，将2022年65岁及以上老年人口数量及其占比数量作为参考序列X0（k）=X0（1），X0（2），...，X0（22），选取的8个影响因素作为比较序列Xi（k）=Xi（1），Xi（2），...，Xi（22）（i=1，2，...，8）。

第二步，无量纲化处理，得到新序列Y0（k）=Y0（1），Y0（2），...，Y0（22）和Yi（k）=Yi（1），Yi（2），...，Yi（22）（i=1，2，...，8）。

第三步，计算差序列△i0（k）=|Y0（k）-Yi（k）|（i=1，2，...，8，k=1，2，...，22）。

第四步，计算极大差M=maxi maxk△i0（k）和极小差m=mini mink △i0（k）。

第五步，计算关联系数ri0（k）=（m+ρM）/（△i0（k）+ρM）（ρ∈[0，1]），这里取ρ=0.5。

第六步，计算关联度r（X0，Xi）=" ri0（k）/n。

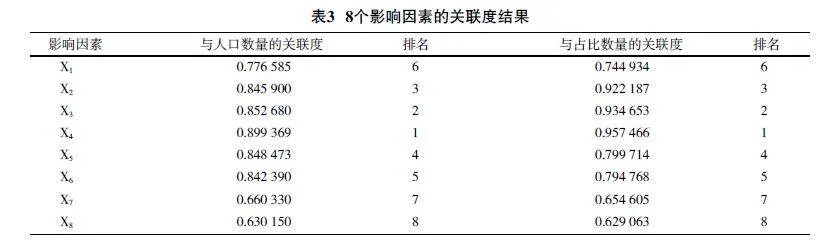
由下页表3可以看出，8个影响因素的关联度都大于0.5，说明选取的8个指标对于广东省老年人口数量及其占比均有明显影响，影响程度均为：X4gt;X3gt;X2gt;X5gt;X6gt;X1gt;

X7gt;X8。其中，城镇化率和死亡率与老龄化的关联度很高，均达到了0.85以上，对老龄化的影响很大。随后的出生率、卫生技术人员数、医疗卫生机构床位数和人均GDP与其关联度也达到0.75以上，也将会对老龄化产生较大的影响。

（四）主成分分析

1.基本思想

主成分是被选择出的比原始变量个数少，却能解释大部分数据信息的几个新变量。主成分分析就是研究多个变量间相关性并进行应用的一种多元统计方法，该方法通过较少的变量（几个主成分）来解释多个变量间的相关信息。即从原始变量中推导出少数几个主分量，使它们尽可能多地保留原始变量的信息，且主成分间互不相关。具体来说，主成分分析就是在尽量保证不丢弃任何变量信息的情形下，将n维特征值映射到k维上（klt;n），而重新构造出来的k维正交特征值就称为主成分。

对某一问题假设有P个指标，分别记为X1，X2，...，Xp由这些随机变量构成的随机向量记为X=（X1，X2，...，Xp）T，对X进行线性变换可以得到组合变量F。主成分分析的一般模型为：

F =a X +a X +...+a X F =a X +a X +...+a X ...F =a X +a X +...+a X

其中a2i1+a2i2+...+a2ip=1，Fi为第i个主成分（i=1，2，...，P）。

2.具体步骤

第一步，选取初始分析变量。根据对广东省人口老龄化影响因素的灰色关联分析，选取了X1人均GDP（万元）、X2出生率（%）、X3死亡率（%）、X4城镇化率（%）、X5卫生技术人员数（万人）、X6医疗卫生机构床位数（万张）、X7基本养老保险支出（亿元）、X8基本医疗保险支出（亿元）共8个因素作为初始分析变量。

第二步：判断是否需要进行无量纲化处理。主成分分析对于初始变量的方差非常敏感，如果初始变量的取值范围之间存在较大差异，将会造成分析结果存在较大偏差，所以需要采取措施将数据转换为可比较的尺度，即要对数据进行无量纲化处理。常用的方法有标准化、极值化和均值化等。通过观察，可以发现这8个初始变量的取值范围相差较大且度量指标各不相同，故需要对数据进行无量纲化处理，这里选择标准化处理。

第三步，进行适配性检验。这里采用KMO检验法和巴特利特球形检验法。KMO检验法是通过比较样本各变量间的简单相关系数和偏相关系数的大小来判断变量间的相关性。若偏相关系数远小于简单相关系数，则认为变量间的相关性较强。巴特利特球形检验法的原假设是相关系数矩阵为单位阵，认为各变量之间是线性无关的。若拒绝原假设，则认为各变量之间是线性相关的。在进行适配性检验时，可得KMO统计量的值为0.744，大于0.6，对应的因子分析情况为合适，说明各个变量之间存在相关性。同时，巴特利特球形检验的概率P值为0.000，小于显著性水平0.05，应当拒绝原假设，即认为相关系数矩阵与单位矩阵存在显著的差异。二者均说明了原始数据适合做主成分分析。

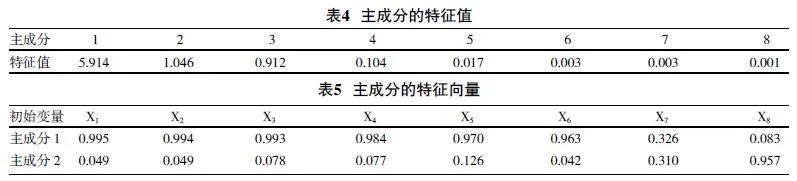
第四步，计算特征值（见表4）和特征向量（见表5）。根据特征值和特征向量可以进一步求出对应主成分的线性表达式。

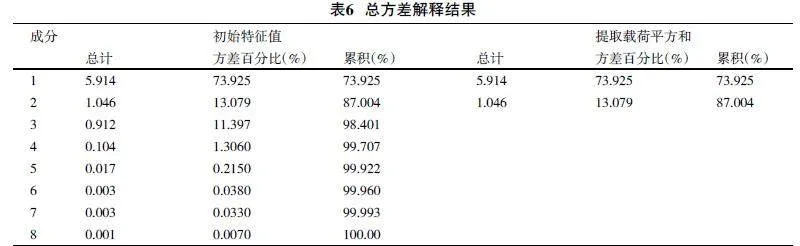
第五步，判断特征值是否大于1。只有当某个主成分的特征值大于1时，主成分从初始变量的组合中提取的信息才能比单一的初始变量多。而只有主成分的累计方差贡献率大于80%时，才能反映出全部初始变量的信息。若达不到标准，则说明数据不适合做主成分分析，需要另选其他方法。由表6可以看出，第一主成分的特征值为5.914，第二主成分的特征值为1.046，均大于1，并且第一和第二主成分的累积方差贡献率为87.004%，大于80%，说明第一和第二主成分已达到主成分分析的要求。

第六步，确定主成分个数，得到线性表达式。即Fi=wi1Xi1+wi2Xi2+...+wipXip，wipθpi / 表示各个初始变量的系数，θpi 表示第i个主成分对应第P个初始变量的系数， 表示第i个主成分特征值的平方根。因此，主成分F1和F2的线性表达式分别为：

F1=0.408X1-0.134X2+0.034X3+0.399X4+0.409X5+

0.409X6+0.396X7+0.404X8

F2=-0.077X1-0.303X2+0.935X3-0.123X4-0.048X5-

0.048X6+0.041X7+0.075X8

3.结果分析

分析主成分F1可知，人均GDP、城镇化率、卫生技术人员数、医疗卫生机构床位数、基本养老保险支出和基本医疗保险支出这6个变量的载荷量较高，它们能够反映一个地区的经济发展水平，因此可称F1为经济发展因素。一般来说，一个地区经济发展水平越高，该地区的人均GDP和城镇化率也越高。与此同时，经济水平的提升也会增加医疗资源，卫生技术人员数和医疗卫生机构床位数也会随之增加。有了可靠的医疗资源和增加的收入作保障，老年人会增加基本医疗与养老保险支出，从而提高生活质量和医疗保障水平，便会延长平均预期寿命。

分析主成分F2可知，出生率和死亡率这两个变量的载荷量较高，它们能够反映一个地区的人口结构变化，因此可称F2为人口结构因素。2000—2015年人口出生率缓慢下降，幅度不大。在2015年实施“全面二孩”政策后，2017年的出生率较2015年增长了2.56%。但在此轮生育高峰过后，从2018年开始出生率便逐年下降，截至2021年底已经跌至9.5%。显然，当前广东省面临着的是较低的出生率和死亡率，未来人口老龄化现象会进一步加剧。

三、结论

第一，GM（1，1）模型预测结果表明，未来广东省65岁及以上老年人口数量及其占比将呈现逐年递增趋势。预计到2035年，65岁及以上老年人口数量将达到1 584.735 2万人，占比将达到9.971543035%。人口老龄化现象日益严重，不仅会给经济带来新的挑战，还将增加中青年的负担。不过，也要理性看待模型的预测结果，不同方法、不同时期的数据以及模型拟合过程中产生的误差，都会对预测结果产生不同的影响。但是，在未来老龄化程度不断加深、老年人口不断增加是相同的研究结果。

第二，灰色关联分析结果表明，城镇化率和死亡率与老龄化的关联度较高，对老龄化的影响效果较为显著。城镇化率越高意味着该地区现代化程度越高，能在一定程度上代表当地的经济发展水平以及生活水平，并且城镇化率能在一定程度上影响医疗保障水平，进而影响死亡率。其次是出生率、卫生技术人员数、医疗卫生机构床位数和人均GDP与老龄化的关联程度。人均GDP作为衡量经济发展水平的重要指标，它的提高标志着经济水平的提升，可以为老年人提供坚实的养老保障。经济越发达，卫生技术人员数与医疗卫生机构床位数等基础医疗水平会越好，能使人均寿命延长。出生率降低会使老龄人口占比提升。基本养老保险与医疗保险支出同样对老龄化有重要影响，因为它们涉及老年人退休后享有的待遇和报销的医疗费问题，能够为他们提供基本的生活和医疗保障。

第三，主成分分析结果表明，影响广东省人口老龄化的主成分可以分为经济发展因素和人口结构因素。其中人均GDP、城镇化率、卫生技术人员数、医疗卫生机构床位数、基本养老保险支出和基本医疗保险支出这6个变量可归为经济发展因素。人均GDP和城镇化率都是衡量经济发展的重要指标。经济发展水平的提高，可以促进卫生技术人员数和医疗卫生机构床位数的增长，可以为老年人提供更坚实的养老和医疗保障。同时，老年人的基本养老保险支出和基本医疗保险支出也会随之增加，从而延长老年人口的平均寿命。出生率和死亡率这两个变量可归为人口结构因素。随着现代社会的发展，平均受教育水平的提高，越来越多的年轻人从早婚早育、多子多孙的观念转向了晚婚晚育、少生优育的观念，不断降低的出生率会直接影响老年人口的占比。现代养老保障和医疗服务体系的不断发展，也使得老年人能够得到较好的生活和医疗保障，平均预期寿命相应延长，老年人口数量相应增加。

参考文献：

[1]" "David E，Bloom，et al.Implications of Population Ageing for Economic Growth[J].Oxford Review of Economic Policy，2010，26（4）：583-612.

[2]" "Dall，Timothy M，et al.An Aging Population And Growing Disease Burden Will Require A Large And Specialized Health Care Workforce By 2025[J].Health Affairs，2013，32（11）：2013-2020.

[3]" "韩鹏，宋晓晓.基于灰色理论的内蒙古人口老龄化趋势预测及其影响因素研究[J].干旱区资源与环境，2023，37（1）：44-51.

[4]" "杨华.基于灰色神经网络组合模型的人口老龄化预测研究[D].重庆：重庆工商大学，2022.

[5]" "胥俊林，陈友军.基于新陈代谢灰色模型对人口老龄化的预测[J].四川文理学院学报，2023，33（2）：47-53.

[6]" "Walford N S，Kurek S.A Comparative Analysis of Population Ageing in Urban and Rural Areas of England and Wales，and Poland over the last Three Census Intervals[J].Population Space amp; Place，2010，14（5）：365-386.

[7]" "田甜.西部地区人口老龄化时空演变及影响因素[J].市场周刊，2023，36（5）：17-20.

[8]" "胡琼，罗娟.上海人口老龄化发展趋势及影响因素研究：基于灰色理论[J].经济研究导刊，2021，491（33）：52-54，151.

[9]" "陈宁.全面二孩政策实施对我国人口老龄化的影响研究[J].华中科技大学学报（社会科学版），2017，31（2）：96-103.

[10]" "刘思峰，党耀国，方志耕，等.灰色系统理论及其应用（第五版）[M].北京：科学出版社，2010.

[11]" "龚家强.用EXCEL实现VCF值的自动查找及插值计算[J].大众科技，2013，15（6）：11-14，5.

Prediction of Population Aging Trend and Influencing Factors in Guangdong Province Based on Grey Theory

CHEN Siyuan， WANG Minghui， YU Yuekai， CHEN Xunhua

（School of Mathematics and Statistics， Shaoguan University， Shaoguan 512005， China）

Abstract： The aging of China's population continues to intensify， which has a profound impact on all areas of economic operation， all links of social construction， social and cultural aspects， as well as national comprehensive strength and international competitiveness. Therefore， taking the aging population of Guangdong Province as the research object， based on the GM （1，1） model， this study explores the changing trend of the number and proportion of elderly population from 2022 to 2035. Using grey relational analysis and principal component analysis methods， analyze the 8 factors that affect aging and identify the main influencing factors. The results indicate that the number and proportion of elderly people aged 65 and above will show an increasing trend year by year in the next 14 years. It is expected that by 2035， the number of elderly people aged 65 and above will reach 158473500， accounting for 9.971543035%; urbanization rate， mortality rate， birth rate， number of health technicians， number of beds in medical and health institutions， and per capita GDP are six important factors affecting aging; economic development factors and population structure factors are the two main components that affect aging.

Key words： Population aging; GM （1，1） model; Grey correlation analysis; Principal component analysis; Influencing factors

[责任编辑" "妤" "文]