基于GA优化神经网络的变刚度复合材料板簧刚强度预测研究

关键词：SMA驱动器;空间布置参数;BP神经网络;遗传算法;寻优效率

0 引言（Introduction）

为顺应汽车低碳、轻量化[1]及智能化[2]的发展趋势，将具有形状记忆特性的镍钛合金丝（SMA）植入三维编织体中形成SMA驱动器，再将其模块化并植入汽车钢板弹簧中，可以在温度激励下实现变刚度驱动[3-4]。通过优化植入驱动器的性能和空间布置参数，可以得到最佳变刚度效果和强度，然而在SMA驱动器模块化植入大型板式结构以实现工程应用的过程中，如何提高优化算法效率是首先要解决的问题。

目前，为了提高模块化元件布设参数寻优算法的效率，相关学者尝试将智能算法应用到模块化元件布设参数的寻优中[5-6]，但上述智能算法在处理大型结构时，都会不可避免地遇到由于布设点的增加、驱动器数量增加等所导致的搜索点过多及目标函数值计算次数过多、时间较长的问题。

基于上述问题，本文提出了采用BP神经网络[7]预测的方法代替传统的对目标函数值进行直接计算的方法[8]，并针对BP神经网络易收敛在局部极小值而得不到全局最优的缺点，进一步通过遗传算法对BP神经网络模型进行改善，以提高预测精度，进而提升对于大型板式结构中驱动器最优空间布置参数的寻优效率。

1BP神经网络模型建立（Establishment of BPNeural Network model）

1.1 数据来源

鉴于篇幅所限，刚度和强度的详细理论计算将在另一篇论文中深入阐述。但是，本文会引用相关的Matlab计算程序作为支持数据集。

1.2BP神经网络基本原理

BP神经网络（Back Propagation Neural Networks）是一种多层的前馈型神经网络，由于其对误差的调节是从输出层逐步往回推进，因此又被称为误差反向传播网络。BP神经网络一般由3个神经元层组成，分别为输入层、隐藏层及输出层。BP神经网络通常采用全连接方式，同一层的神经元互不干扰，不同层之间的神经元通过权值等网络结构参数实现非线性连接。传统BP神经网络算法具体分为以下两个过程[9]。

第一阶段是信号的正向传播过程：将对象的特征信号经由输入层开始正向传递，不同的自变量x1，x2，…，xi 对应不同的权重系数w1，w2，…，wj，为了使模型更好地收敛，引入偏置项自变量x0 为恒定值-1，对应的权重系数为θ，将所有的自变量乘以各自对应的权重系数后求和得到b，将b 经过激活函数处理后得到ϕ（b），上一层神经元的输出元又作为下一层的输入，如此进行一系列非线性变换，经由隐藏层神经元传递到输出层神经元，最后将得到的输出信号与目标输出信号进行误差对比分析，若达不到条件，则转入误差的反向传播过程。

第二阶段是误差的反向传播过程：输入层x1，x2，…，xi将信号经由隐藏层正向传播到输出层后，得到的预测输出x1，x2，…，xi 与真实值x1，x2，…，xi 之间存在误差，为了缩小预测输出与真实输出之间的误差，将误差从输出层开始，按照正向传播时的权重系数进行反向传播，从而根据算法策略对权重系数进行修正。如此循环往复正反向传播，权重系数得到不断的更迭，直到前向传播达到期望输出，即误差达到一个满意值。此时，神经网络模型完成训练，可直接对其他样本进行预测。

1.3BP神经网络参数设置

BP神经网络的输入层是影响板簧刚强度的主要因素，用X 表示;输出层是影响板簧静态性能的主要因素，用Y 表示。其分别可以表示如下：

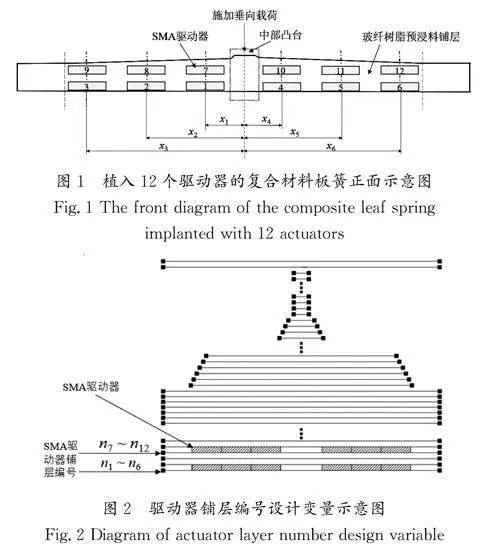
其中：x1，x2，…，x6 为驱动器在板簧中的横坐标，植入12个驱动器的复合材料板簧正面示意图如图1所示。n1，n2，…，n12为驱动器在板簧厚度方向中铺层的铺层位置编号，驱动器铺层编号设计变量示意图如图2所示。Δk 为板簧在通电前后的变刚度效果，称其为第一目标（T1）;R 为板簧的结构强度比，称其为第二目标（T2）。

在BP神经网络模型中，输入层各因素对输出层各因素的影响程度取决于输入层各影响因素的权重，通过BP神经网络的自主学习能力，网络不断进行自我训练和调节，使最终的网络输出值不断逼近实际值。模型的训练基于Pytorch深度学习框架，采用留出法（Holdout）进行验证，将整个数据集随机分成两个部分，完整的数据集有8 000组，其中7 920组数据作为训练集，80组数据作为测试集。使用SGD（随机梯度下降策略）优化算法更新训练数据中的网络权重。损失函数采取均方误差（MSE）来衡量训练过程中预测值与真实值的匹配程度。隐藏层使用激活函数ReLU，输出层使用线性激活函数。本文还考虑了网络拓扑和学习率对模型性能的影响，并开发了几种网络模型，这些模型的隐藏层层数和神经元数量各不相同，根据经验公式判定隐藏单元数的大概取值范围，进而通过试错法确定最佳网络结构，经验公式如下：

其中：n 为输入层单元数量，m 为输出层单元数量，α 为1～10的常数。

常见的回归模型一般使用R2 系数和RMSE 评估回归模型的性能。其中，R2 系数又称拟合优度，通常被用来描述数据对模型拟合程度的好坏，表示自变量对因变量的解释程度，值域在[0，1]之间，越接近1，说明回归拟合效果越好。RMSE 为均方根误差，它衡量了预测值与真实值之间的均方根差异，表示预测值与真实值之间的平均偏差程度。R2 系数和RMSE的计算公式如下：

为了获得泛化性能良好的模型，需要合理设置完整遍历数据集的次数，若遍历次数过少，则有可能发生欠拟合（对于定性数据的学习不够充分），若太多，则容易发生过拟合（泛化能力不足，在非样本的数据上表现很差），所以本文引入提前停止功能，在每次遍历结束后进行一次误差检查，如果200次遍历中，某次迭代下误差未得到1e-6的改善降低，便提前停止训练。

1.4 训练结果总结与讨论

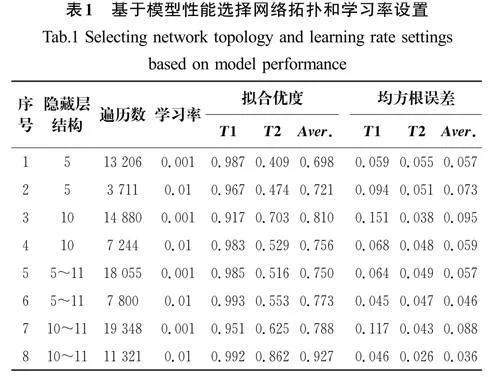
在训练过程中，研究人员尝试调整损失权重（各个目标损失在总损失中的占比），但是发现这类改变对于拟合效果的改善效果微乎其微，表明两个输出之间的任务关联性较强，存在一定的依赖关系，所以网络会自动适应重要性不同的任务。本文虽然通过加权求和得到总损失，但是不会考虑损失权重的影响，在BP神经网络模型中将其设置为1∶1。输入层神经元数量恒定为18个，输出层神经元数量恒定为2个，由此对不同隐藏层的层数、不同隐藏层的神经元数量及不同学习率的模型进行了性能评估，基于模型性能选择网络拓扑和学习率设置如表1所示。

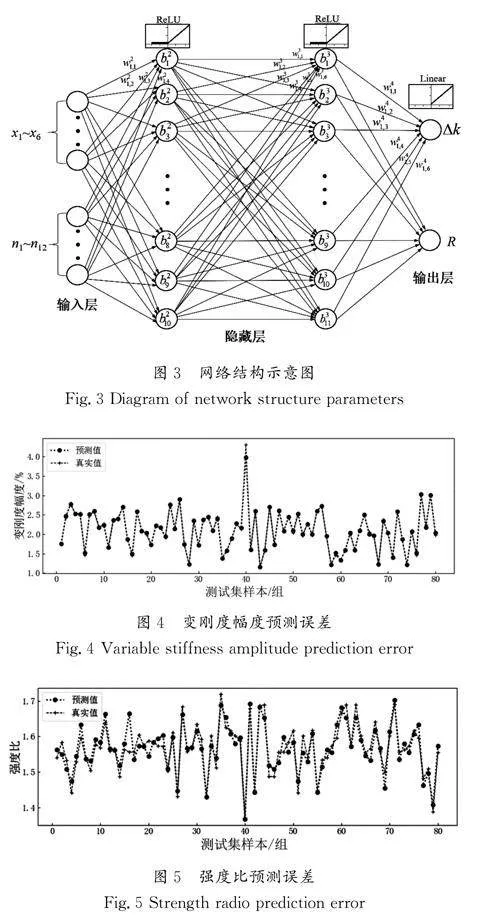
从表1中的数据可知，在经验公式给出的范围内，当学习率和隐藏层层数保持一致时，增加隐藏层神经元数量能够在一定程度上提升网络性能。通常，学习率越小，意味着极值点越不容易被忽略，但也可能导致进入局部极值点就收敛，并大幅降低收敛速度;学习率过大，意味着有可能找不到极值点，容易在最优解附近振荡。由表1可知，学习率越大对本文所提网络的性能改善效果越好，并且具有较快的训练速度。综上所述，表1中序号8的网络结构和参数为最佳模型，其网络结构示意图如图3所示，测试集中预测结果与真实值的对比如图4和图5所示。描述T1的预测效果的R2 系数达到了0.992，RMSE仅有0.046。描述T2的预测效果的R2 系数达到了0.862，RMSE仅有0.026。在本文中，T1作为主要目标，传统BP神经网络对其预测效果也比较理想，而对T2的预测效果则稍显不足，因此还需对模型进行改进。

2 GA-BP 算法模拟分析（GA-BP algorithmsimulation analysis）

2.1 GA-BP算法概述

BP神经网络中存在隐藏单元，虽然在训练过程中采用了梯度下降的策略对权值进行更新，但是由于无法保证误差全局最小，因此网络的权值和阈值可能并非最优。尽管BP神经网络模型已经具备一定的预测精度，但是为了更准确地预测板簧的静态性能，本研究采用遗传算法（GA）[10-11]替代梯度下降策略对BP神经网络模型的权重和阈值进行优化。遗传算法基于遗传学的原理，以遗传学为理论基础，通过模拟群体中个体的选择、交叉和变异等过程，逐步优化问题。引入GA优化BP神经网络可以很好地解决在BP神经网络中初始权重选择范围大、误差无法获取到全局最小值等问题，从而得到一个预测性能和精度更好的网络模型[12]。

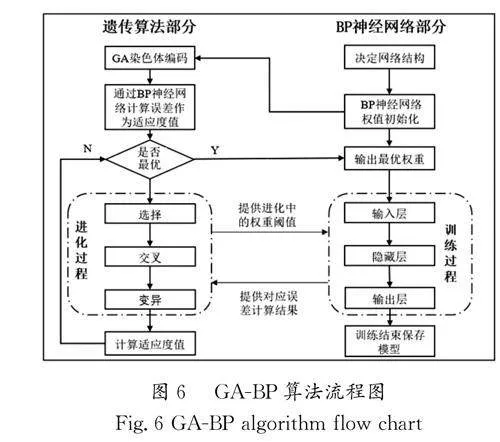
使用GA优化BP神经网络分为以下3个部分：①BP神经网络结构的确定;②使用GA进行权值训练;③进行GA-BP神经网络模型预测。在已经确定了神经网络模型结构的基础上，研究人员采用遗传算法进一步优化BP神经网络的权值和阈值，在此过程中，每个遗传算法的个体均涵盖网络的所有权值和阈值，其适应度通过特定的适应度函数进行计算。遗传算法通过选择、交叉、变异等操作，筛选出最优适应度值的个体。BP神经网络预测利用遗传算法得到的最优个体分配网络的初始权值和阈值，然后用这些数据训练网络，最终获得预测模型的输出。GA-BP算法流程图如图6所示，GA-BP优化步骤如下。

（1）染色体编码。根据前文建立的变刚度复合材料板簧性能预测BP神经网络，将其所有的权值和阈值作为染色体的基因片段，采用分段的实数编码方式，每个染色体都是一个实数串。所有基因形成染色体向量V=[v1，v2，…，vk，…，vn]，其中[v1，v2，…，vk]是染色体的权重基因，[vk +1，…，vn ]是染色体的阈值基因。

（2）种群初始化。通过BP神经网络权值和阈值随机初始化生成对应种群规模的染色体数量。

（3）适应度函数构造。遗传算法是通过适应度函数模拟大自然中的“适者生存”机制，因此适应度函数要能有效地指导整体优化方向，并且保证不会陷入局部最优或者搜索不收敛的情况。为提升BP神经网络的泛化能力，在混合训练中，本文以所有目标样本的误差平方和作为染色体个体的适应度值，以获取更优的初始权值，其公式如下：

其中：yi 是BP神经网络第i 个输入特征下的板簧性能的期望输出值，y^i 是第i 个输入特征下的板簧性能的预测输出值，N为目标样本总数。

（4）选择策略。遗传算法的选择策略有很多种，例如轮盘赌法和锦标赛法。本文中选择轮盘赌法，具体而言，采用了基于适应度大小进行选择的概率分配方法，其公式如下：

其中，Fi 为个体的适应度值。由于本文中适应度值代表的是期望输出与预测输出的误差大小，因此该值越小越好，但在轮盘赌中适应度越大的个体，被选中的概率更高，因此在个体选择之前，需要将适应度值进行转换，本文进行了倒数处理。fi是转换后的个体适应度值，pi 是每个个体在轮盘赌中被选择的概率。

（5）交叉策略。由于本文采用实数编码的方式对个体进行染色体编码，交叉操作方法采用简单的单点交叉方式，通过选择策略筛选出的个体进行随机配对，分成父代和母代，再通过随机选择交叉点进行基因交换。值得一提的是，为了更好地保证种群的多样性，本文引入交叉概率，满足条件则进行如上的单点交叉方式，不满足条件则直接返回父代和母代。

2.2 参数设置

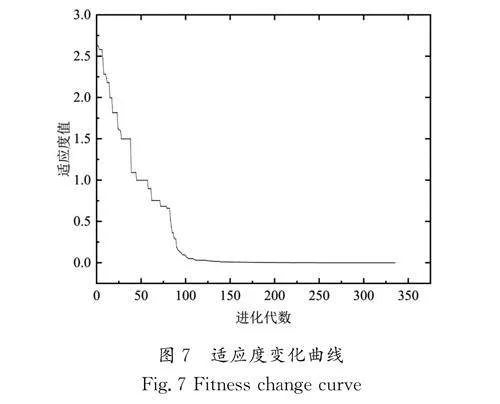
在已训练好的网络结构上，采用遗传算法对权重进行更新迭代，搜索使目标损失最小的预测模型参数，鉴于本文的模型为多输出类型，遗传算法的适应度计算，即目标损失，是通过加权和的方式来确定的。对于变刚度复合材料板簧而言，变刚度效果为首要满足目标，因此将权值设置成第一目标（变刚度效果）为0.6，第二目标（结构强度）为0.4。初始化时，设置迭代次数为1 000次，种群大小为300，选择策略采取轮盘赌法，交叉策略采取单点交叉，交叉概率设置为0.95，变异概率为0.1，经过345次迭代后获得最优结果，其中适应度变化曲线如图7所示。

2.3 模型评估性能对比

为了更好地观测预测效果与真实值的误差，引入绝对误差计算，公式如下：

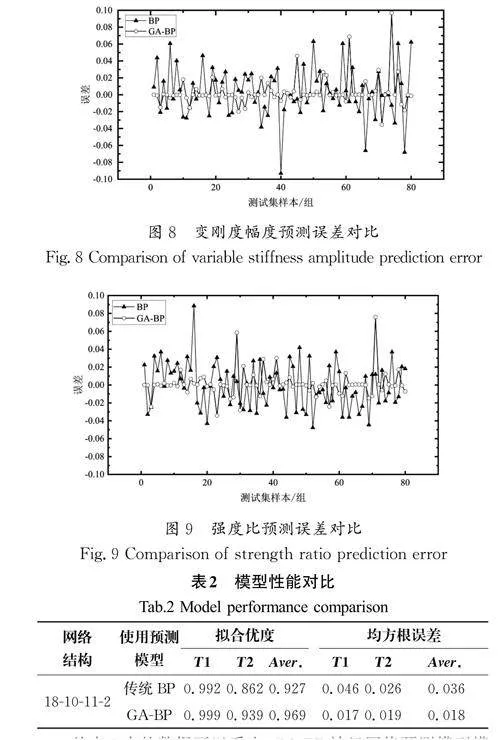
其中：y^为预测输出值，y 为真实输出值。两个目标的两种方法预测误差对比如图8和图9所示。

对比传统BP神经网络预测误差和GA-BP神经网络的误差，评价指标结果如表2所示。

从表2中的数据可以看出，GA-BP神经网络预测模型模拟的拟合优度为0.969，比传统BP神经网络预测模型提高了4.5%，均方误差降低了50%，GA-BP神经网络预测结果误差较小，更接近期望目标值，优化效果明显。

从图8和图9中可以看出，对于两个目标而言，大部分误差均处于±0.04范围内，少数达到了±0.06以上，总体符合预测精度要求，并且在大部分测试样本中，相较于传统单一使用BP神经网络模型，经过GA优化的BP神经网络模型的预测结果误差更小，更接近真实值，并且具有更准确的变刚度复合材料板簧性能预测结果。

2.4 优化速度对比

将拟合好的神经网络模型导入Matlab中，与变刚度复合材料板簧的理论模型直接进行计算对比，综合考虑优化目标变刚度效果和结构强度，对每个驱动器的空间布置参数进行遗传算法寻优，分为传统遗传算法寻优（每次迭代种群中的个体目标值通过理论模型计算得到），GA-BP-GA算法寻优（每次迭代种群中的个体目标值通过预测模型得到）。在相同的计算机配置下优化效率对比如表3所示。

从表3中的数据可知，使用GA-BP神经网络对个体进行预测代替传统的对于目标函数值的直接计算，在单次目标值的计算中效率提高了172倍，在总体空间位置寻优中同样大大提高了效率，优势明显。并且，寻优得到的驱动器空间布置参数完全一致，符合优化结果。在更大的板式结构中，随着驱动器数量和可选位置的增加，寻优效率的提升效果将更加明显。

3 结论（Conclusion

本文基于传统智能算法寻优效率低的缺点，提出GA-BP 神经网络方法，并针对变刚度复合材料板簧中驱动器的空间布置情况进行了分析，通过对比两个方法对于性能目标的拟合优度和均方根误差，相较于传统BP神经网络方法，经过GA优化的BP神经网络预测模型的预测精度更高，均方根误差和平均误差更小，优化效果明显，并且其多目标平均预测精度达到96.9%，满足要求。此预测方法相较于传统智能算法大大提升了空间位置的寻优效率，为大型板式结构的寻优效率的提升提供了有益的参考。