EGM2008全球重力场模型在输电线路工程中的应用

第一作者简介：刘丰（1982-），男，工程硕士，高级工程师。研究方向为电力勘测。

*通信作者：陈西强（1987-），男，硕士，高级工程师。研究方向为电力勘测。

DOI：10.19981/j.CN23-1581/G3.2024.21.037

摘" 要：针对输电线路工程所需的正常高，该文介绍基于EGM2008全球重力场模型来获取待定点正常高的直接法、均值法、高差法基本原理，结合某一特高压输电线路工程进行应用分析，得出直接法无法满足输电线路工程的应用要求，而均值法和高差法能够满足输电线路工程规程规范要求，且均值法和高差法在整体应用上精度一致。高差法在选取基点后，正常高获取的精度与基准点在空间距离上呈现一定的相关性，在有多余已知控点的情况下，应分段选取基点，保证每个基点的控制范围在30 km以内。

关键词：EGM2008；输电线路；直接法；均值法；高差法

中图分类号：P223" " " 文献标志码：A" " " " " 文章编号：2095-2945（2024）21-0156-04

Abstract： In view of the normal height required by transmission line engineering， this paper introduces the basic principles of direct method， mean method and height difference method based on EGM2008 global gravity field model to obtain the normal height of a certain UHV transmission line project. It is concluded that the direct method can not meet the application requirements of transmission line engineering， but the mean method and high difference method can meet the requirements of transmission line engineering specifications， and the accuracy of the mean value method and the height difference method are the same in the whole application. After selecting the base point of the height difference method， there is a certain correlation between the accuracy of the normal height acquisition and the reference point in the spatial distance. In the case of excess known control points， the base point should be selected in stages to ensure that the control range of each base point is less than 30 km.

Keywords： EGM2008; transmission line; direct method; mean value method; height difference method

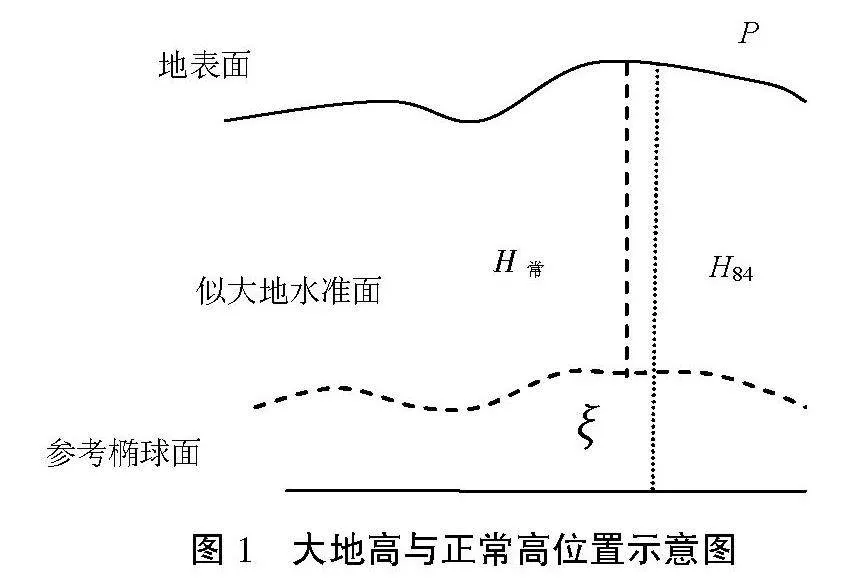
输电线路工程中高程基准通常采用1985高程基准，均属于正常高。目前主要采用GNSS定位技术，结合高程转换参数获取待定点的正常高，但GNSS所获取的直接高程为大地高H84，其是相对于WGS84参考椭球面的高度，与正常高H常存在的差值称为高程异常，三者直接的关系如图1所示。

图1" 大地高与正常高位置示意图

EGM2008全球重力场模型结合当前能够快速获取地表某点的GNSS大地高和平面位置，为快速获取工程所需的正常高提供了新的思路。EGM2008全球重力场模型在中国大陆区域的总体精度为20 cm，华东华中地区12 cm，华北地区达到9 cm，西部地区为24 cm[1-2]，其精度与地形复杂程度成反比，地形平坦的东部模型精度最高，西部最低，且高程异常转换精度主要取决于GPS大地高的精度，点位精度对其影响不大[3]。有关学者研究表明，在铁路勘察、水利水电等工程应用中，对不同地形条件采用EGM2008全球重力场模型结合少量水准高程，通过高差法消除其与局部大地水准面直接的系统差，可在一定程度上取代水准测量，满足大比例尺测图的计算要求[4-8]。

本文研究EGM2008全球重力场模型的高程异常获取直接法、均值法、高差法，介绍了其求取的基本原理和实现方法，并对其精度通过误差传播定律进行了初步分析，最后通过某特高压工程实践，比较3种方法的精度及应用场景，得出有益于输电线路工程中高程异常快速高精度求取方式，为输电线路工程高程控制提供参考价值。

1" 正常高求取方法

基于EGM2008全球重力场模型的高程异常获取方法是由地球挠动位的球谐函数级数展开式求高程异常ξm，结合GNSS获取的高精度大地高，再求出点的正常高的一种方法。

由物理大地测量学可知，地面点P的挠动位T与该点引力位V和正常引力位U之间的关系为

T=V-U。" " " （1）

而地面点P的高程异常ξm为

ξm=T/r，" " " "（2）

式中：r为地面点P的正常重力值。正常重力值r和正常引力位U可以精确计算，因此只要给出地面点P的引力位V，就可求出地面点P的高程异常ξm。引力位V可由球谐函数级数展开式计算

式中：？籽、B、L分别为地面点的矢径、纬度、经度；Cnm、Snm为位系数；Pnm（sinB）为勒让德函数；n为阶；m为次；GM为地心引力常数和地球质量的乘积，是个常数；A为参考椭球长半轴。

由GPS精确的大地高程与由重力场模型求得的高程异常ξm进行比较，求出该点的正常高程，其原理如下

h=H84-ξm。" " " " "（4）

该方法称为直接法，但相关研究表明，正常高系统与重力场模型之间在某个区域存在一定的系统差[9-14]，通常由GPS大地高程和其水准正常高求得的高程异常ξ与由重力场模型求得的高程异常ξm进行比较，求出该地面点在2个高程系统之间的高程异常差值，如公式（5）所示

？啄ξ=ξ-ξm。" " " " （5）

然后由公共点的平面坐标和高程异常残差值推求其他点的高程异常残差值？啄ξ，由此计算GPS网中未联测水准点的正常高程

h=H84-ξm-？啄ξ。" " " " " （6）

但？啄ξ值的求取方法有2种，第一种是直接由公式（5）求取，即基于EGM2008模型求得高程异常后，由已知点的大地高减去高程异常ξm得到已知点的高程异常残差，当多余1个已知点时，可以将已知点求取的高程异常残差进行平均值计算，将该平均值作为整个区域的均值，记为δξ，称为残差均值法，其他待定点则根据以下公式计算正常高h

h=H84-ξm-δξ。" " " " "（7）

高差法是由已知控制点来确定其中一个作为基点，而其他待定点与基点求差，采取类似水准高差的方式，将高程异常模型之间的系统差通过求差进行消除，从而提高高程异常求取的精度，其原理如下。

确定基点位置。选取离测区中心最近的已知点作为基点位置，其原则如下

根据公式（8）至（10）确定的基准点记为（X0，Y0），采用类似于水准高差的求法，假定同一个测区内正常高与重力场模型之间的高程异常残差是一致的，由此待定点高程hi通过以下方式进行求取

h0=H0-？着m0-？啄？着， （11）

hi=Hi-？着mi-？啄？着。" " "（12）

由公式（11）、（12）推导出

hi=h0+（Hi-H0）-（？着mi-？着m0）。（13）

由式（13）可知，通过对基准点求差后，把正常高系统和重力场模型之间的系统差进行了差分消除，其精度由误差传播定律可知

即未知点的高程精度由未知点大地高的高程精度、重力场模型求取的高程异常精度综合决定。其中，未知点高程精度由实时动态定位（RTK）所采集的高精度GNSS大地高所得，基本在3 cm以内，而重力场模型求取的高程异常精度与地区有关，华北地区可以达到9 cm的精度。由此可知，采用EGM2008全球重力场模型求取正常高的精度总体最优精度应该在9.5 cm。

2" 工程实例分析

某特高压线路工程呈东西走向，西高东低，且位于平原丘陵地区，线路长度约90 km，控制点均匀分布于线路两侧共计18个点。

测区平均高程为67.178 m，最大高程点为最西边的KS11，高程值为139.14 m，根据已知控制点资料，通过以下3种方法进行求取：①直接法，由EGM2008全球重力场模型求取高程异常，根据公式（2）求取，得到高程h1，并与已知值h进行比较，得到高程残差值。②均值法，由EGM2008全球重力场模型求取高程异常，先根据公式（2）求取其高程异常残差值均值，再根据公式（4）直接求取待定点的高程，得到高程值h2，并与已知高程值h进行比较，得到高程残差值。③高差法，根据高差法原理求取待定点高差h3，并与已知高程值h进行比较，得到高差残差值。

由图2分析可知，直接法求取的高程残差值均值为0.425 m，中误差为0.090 m，最大高程残差值为0.471 m，最小为0.185 m，明显不能满足线路工程勘测规范高程较差小于10 cm的技术要求[15]；而均值法的高程较差均值为0.016 m，中误差为0.090 m，最大高程残差值为-0.240 m，最小为0.003 m，且大于10 cm的为KS11、KT01、KT14，均在线路路径途径区域外侧，线路覆盖区域内的高程较差均小于10 cm。高差法的高程较差均值为0.033 m，中误差为0.090 m，最大高程残差值为-0.273 m，最小为0.000 m，且大于10 cm的为KS11、KT01、KT02，相对KT07基点由远而近呈递减趋势，越靠近基点其高程差值越小。

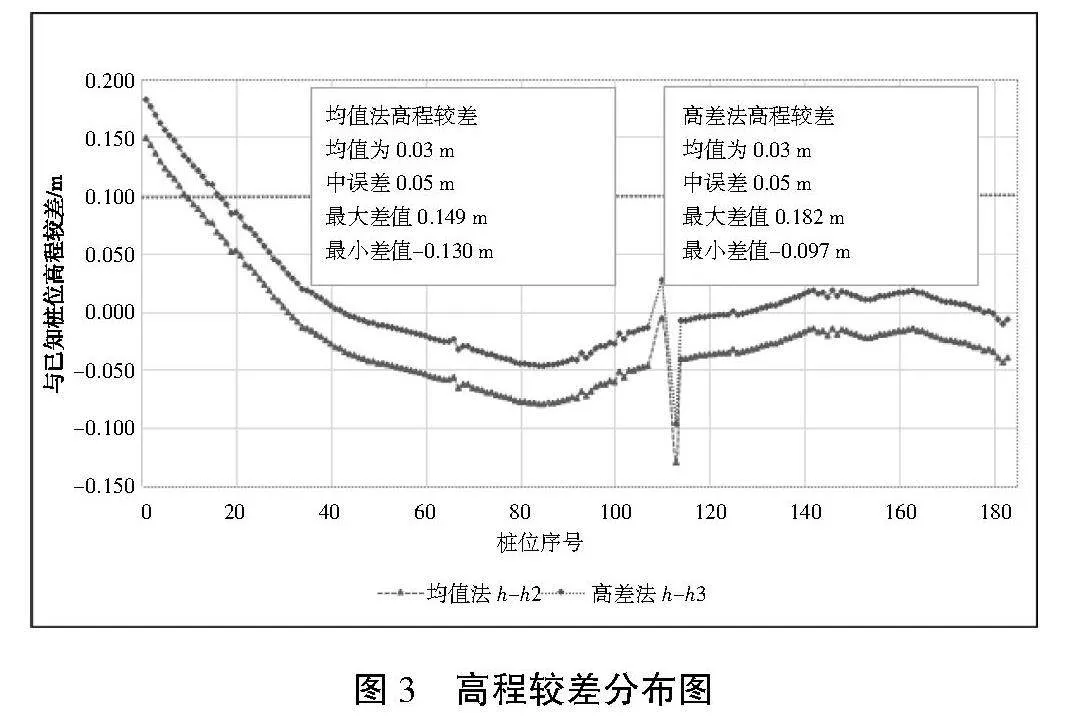
以上分析可知，采用均值法和高差法，对全线中心桩位的高程进行求取，得到已知中心桩位高程h与均值法求取的h2和高差法求取的h3进行做差比较，得到高程较差分布如图3所示。

由图3分析可知，均值法和高差法所求取的正常高与已知桩位高程的差值均值都为0.03 m，且中误差均为0.05 m，整体高程较差分布小于0.1 m，与理论精度分析一致。由此可知，剔除线路起始位置高程起伏大的影响，其余相对平缓的线路路径区域均能满足输电线路规程规范对高程较差的限差的要求。其中，均值法和高差法所求取的正常高整体精度一致。但靠近线路路径所跨区域中心部分高差法求取的精度要比均值法高。

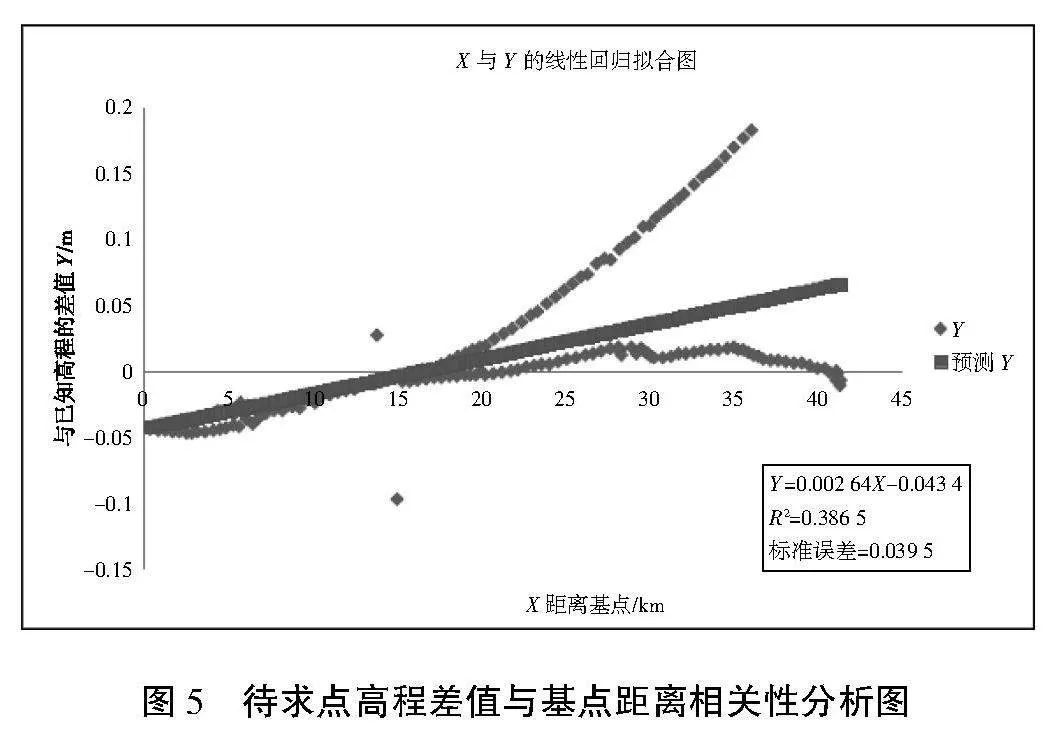
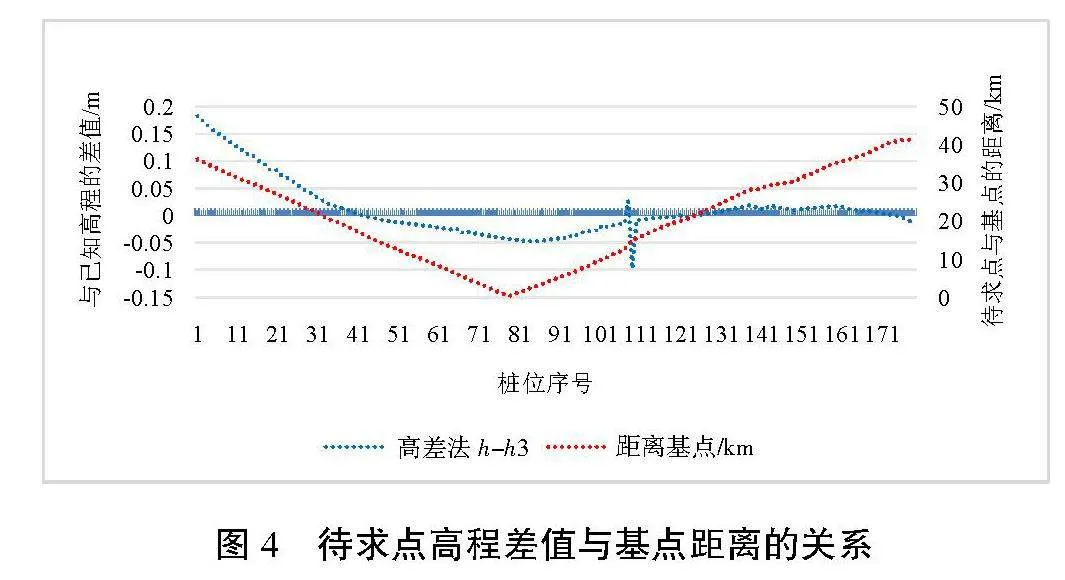
考虑到高差法所选基准点与待求点之间存在一定的距离，其待求点高程差值与基点距离的关系如图4所示，2个因素直接的相关分析如图5所示。

由图4分析可知，高差法所选取的基点在30 km以内均能满足输电线路工程对高程校核差值在10 cm以内的要求，但大于30 km以上，尤其是超过40 km后，其求取差值达到0.169 m，难以满足工程应用需求。同时由图5分析可知，高程法所求取的正常高与已知点高程较差值和距离基点的距离在线性回归分析中，其相关系数为0.386 5，由此说明其相关性并不密切，且在30 km范围其求值误差在5 cm以内。因此建议在有多余已知控点的情况下，应分段选取基点，保证每个基点的控制范围在30 km以内。

3" 结论

本文介绍了基于EGM2008全球重力场模型在输电线路工程中3种高程异常求取方法，分别为直接法、均值法、高差法，其中直接法因正常高程系统与重力场模型所求取的高程异常存在系统性差别，不能直接应用于输电线路工程高程控制及高程获取，而均值法和高差法在某种程度上能够满足输电线路对高程精度的要求，理论最优精度能够达到9.5 cm。

均值法和高差法所求取的正常高整体精度一致，但靠近路径所跨区域中心部分高差法求取的精度要比均值法高。其中，高差法在选取基点后，距离基点由远而近所求取的高程精度越靠近基点精度越高，与基准点高程异常在空间距离上呈现一定的相关性，但不是特别明显。

基于EGM2008全球重力场模型在输电线路工程中应用时，可采用均值法或高差法，但需要注意已知点的内部复核和外部复核检查，均值法宜选取输电线路途径区域内的控制点作为计算依据，而高差法在有多余已知控点的情况下，应分段选取基点，保证每个基点的控制范围在30 km以内。

参考文献：

[1] 杨金玉，张训华，张菲菲，等．EGM2008地球重力模型数据在中国大陆地区的精度分析[J]．地球物理学进展，2012，27（4）：1298-1306.

[2] 章传银，郭春喜，陈俊勇，等.EGM2008地球重力场模型在中国大陆适用性分析[J]．测绘学报，2009，38（4）：283-289.

[3] 张兴福，刘成，王国辉，等.基于EGM2008重力场模型的GPS高程转换方法及精度分析[J].地球物理学进展，2012，27（1）：38－44.

[4] 束蝉方，李斐，郝卫峰.EGM2008模型在中国某地区的检验及适用性分析[J].武汉大学学报（信息科学版），2011，36（8）：919-921.

[5] 许双安.基于EGM2008模型的GPS高程转换方法研究[J].铁道勘察，2012（5）：31-34.

[6] 王作钰.EGM2008重力长模型的高程异常精度分析[J].地理空间信息，2014，12（3）：110-111.

[7] 余宣兴，詹昊，朱明新，等.EGM2008地球重力场模型在GPS高程转换中的应用研究[J].测绘通报，2013（12）：18-20.

[8] 朱亚光，高兴国，常增亮，等.基于EGM2008重力场模型的电厂区高程传递方法研究[J].电力勘测设计，2011（4）：30-32.

[9] 罗陶荣，王中元，梁宁，等.利用EGM2008模型与加权组合模型进行高程异常拟合[J].测绘通报，2018（1）：28-32.

[10] 蔡庆立，卢荣.EGM2008重力场模型在RTK高程测量中的应用[J].全球定位系统，2012，37（4）：71-73.

[11] 翟振和，魏子卿，吴富梅，等.利用EGM2008位模型计算中国高程基准与大地水准面间的垂直偏差[J].大地测量与地球动力学，2011，31（4）：116-118．

[12] 原喜屯.地球重力场模型在GPS高程测量中的应用[J].全球定位系统，2011，36（2）：59-62．

[13] 刘斌，郭际明，史俊波，等.利用EGM2008模型与地形改正进行GPS高程拟合[J].武汉大学学报（信息科学版），2016，41（4）：554-558．

[14] 赫林，李建成，褚永海.1985国家高程基准与全球高程基准之间的垂直偏差[J].测绘学报，2016，45（7）：768-774．

[15] 330 kV～750 kV架空输电线路勘测标准：GB/T 50548—2018[S].北京：中国计划出版社，2018.