河道疏浚工程一维、二维数值模拟比较研究

第一作者简介：石立君（1981-），男，博士，高级工程师。研究方向为土木工程、工程检测鉴定。

DOI：10.19981/j.CN23-1581/G3.2024.21.019

摘" 要：该文通过建立某河道疏浚工程河段平面一维、二维水动力数学模型，对水位进行数值模拟，进而对疏浚前后水位、流速结果进行比较分析。

关键词：一维水动力数学模型；二维水动力数学模型；流速；水位；河道疏浚工程

中图分类号：U616" " " 文献标志码：A" " " " " 文章编号：2095-2945（2024）21-0078-06

Abstract： Through the establishment of the river section plane of a river dredging project， the water level is numerically simulated by using one-dimensional and two-dimensional hydrodynamic mathematical models， and then the results of water level and velocity before and after dredging are compared and analyzed.

Keywords： one-dimensional hydrodynamic mathematical model; two-dimensional hydrodynamic mathematical model; velocity; water level; river dredging engineering

为适应新时期社会经济高质量发展需要，按照问题导向、系统治理的原则，通过对堤防岸坡达标治理、河道清淤疏浚，防汛公路改造消除河段堤防岸坡安全隐患，提升河道防洪和抵抗自然灾害的能力，保障城区防洪安全及社会稳定，改善生态和人居环境，改善流域空气环境质量及水体质量，促进社会经济发展。随着计算机技术的持续进步，数值模拟因其低成本、无比尺效应等优势，在河流运动模拟领域得到了广泛使用，并逐渐替代物理模型试验，变为研究水流运动规律的关键工具。

河流数值模型可分为一维、二维和三维，其中一维数学模型是最早发展的，它以断面平均水流为研究对象，探讨了断面水力要素沿河道变化的特性，常用于分析沿程各断面在洪水演进过程中水位和水量的变化。一维水力学计算方法由于不能反映地表在横向方向起伏变化的影响，在局部河段计算结果可能会出现较大偏差。二维数学模型假设水体的水平尺度远超过垂直尺度，通过不考虑垂直方向上的流速变化解浅水方程，主要用于探究宽浅河道和湖泊的流动分布。三维数学模型求解N-S方程，能够得到详细的三维流场信息，由于计算量大，目前主要用于局部流场的计算，如结构物周围的水动力模拟，很难应用于较大水域的流场计算。

本文结合河道疏浚工程实例，通过河道内一维、二维数值计算的对比，探讨一维水力计算结果与二维水力计算结果的差别。

1" 水流运动数值模拟方法

1.1" 一维数学模型

式中：x、t为距离和时间；A为过水面积；Q为断面流量；Z为水位；？琢为动量修正系数；K为流量模数；qL为旁侧入流。

式中：Z2、Z1为上下断面河床高程；Y2、Y1为上下游断面水深；V2、V1为上下游断面平均流速；？琢2、？琢1为动能校正系数；g为重力加速度；he为工程阻水造成的水头损失。

1.2" 二维数学模型

二维非恒定浅水方程

式中：t为时间；x、y为笛卡尔坐标系坐标；η为水位；d为静止水深；h=η+d为总水深；u、v分别为x、y方向上的速度分量；pa为当地大气压；Ω是柯氏力系数，Ω=2ωsinφ，ω为地球自转角速度，φ为当地纬度；g为重力加速度；ρ为水的密度；ρ0为参考水密度；sxx、sxy、syy分别为辐射应力分量；S为源项；us、vs为源项水流流速。

2" 数学模型建立

2.1" 网格划分

本次数模计算范围为K0+000～K28+700，总长度28.7 km，考虑到水电站的调节作用，计算时将工程河段分为坝下河段1（K0+000～K16+350）和坝上河段2（K16+550～K28+700）2个计算河段。

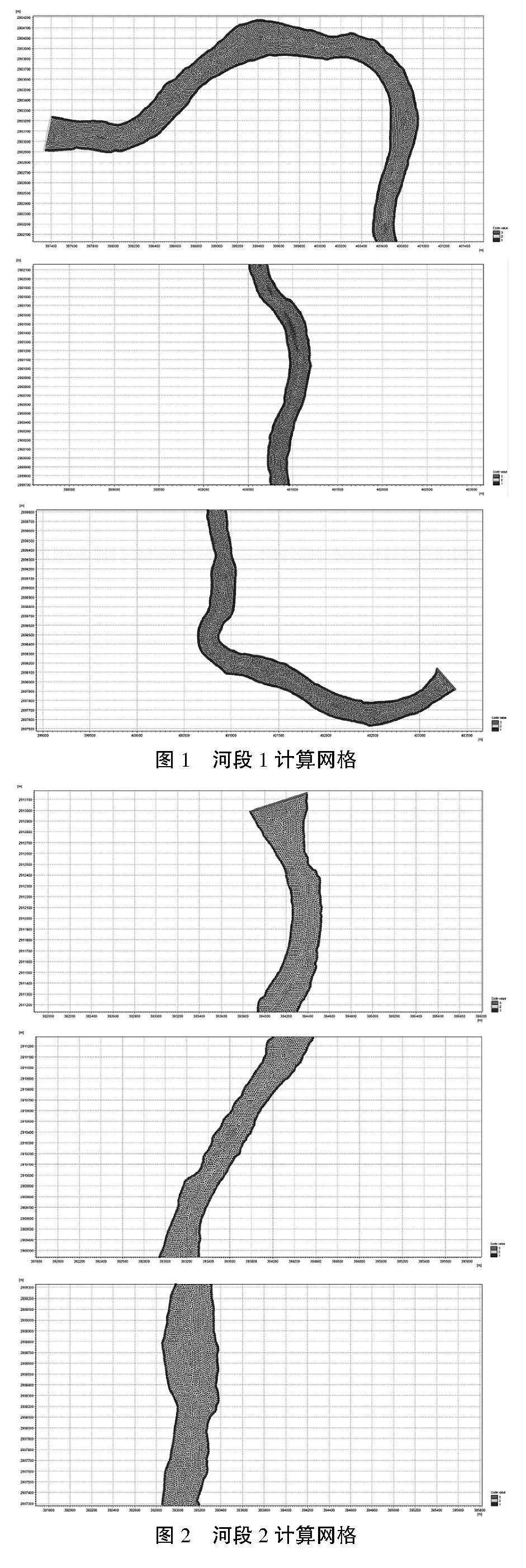
以实测地形资料范围作为网格剖分的边界约束条件，其中包含了河道两岸的大堤。数值模拟计算采用适用性较好的三角形网格进行，坝下河段1和坝上河段2两个河段的计算网格划分如图1和图2所示。为同时保证模型计算的精度和效率，计算范围内河段1共剖分18 898个网格，河段2共剖分13 310个网格。根据地形测点疏密分布情况划分网格疏密，同时对地形变化较大和需重点关注的区域适当加密。

2.2" 地形处理

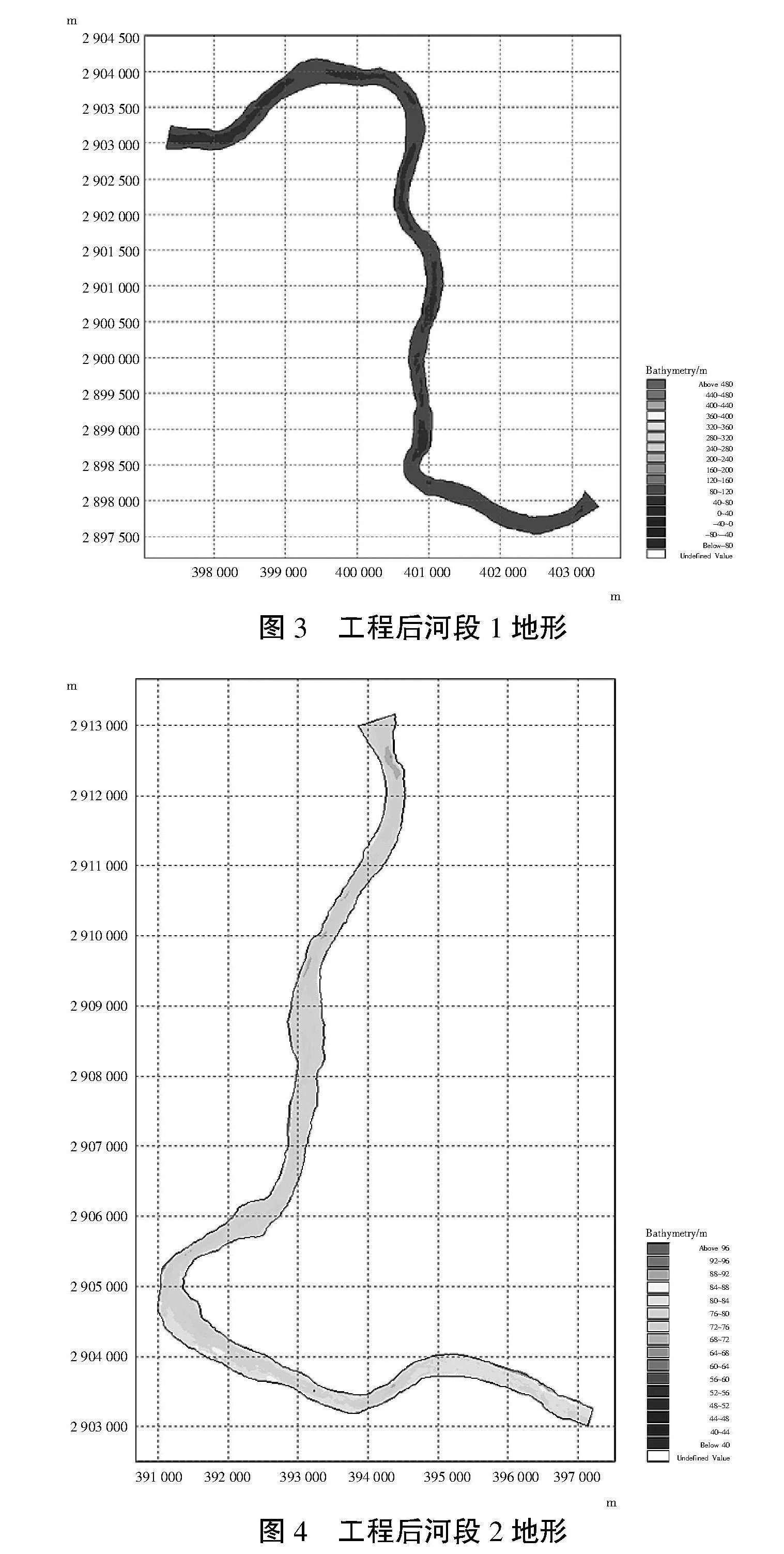
根据《项目初步设计报告》《项目初步设计图册》中各清淤疏浚断面清淤底高程降低相应的网格高程，工程后水电站河段1和河段2地形分别如图3和图4所示。

3" 数模计算分析

选取某山区河流中2个距离较近的河段的疏浚工程进行计算，疏浚在主河槽内进行，主要清除河底淤泥、土层、砂层为主的覆盖层，清淤深度为1～2.0 m。2个河段均位于电站枢纽的上游，河段1长度16.35 km，20年一遇洪水流量为5 090 m3/s，平均枯水流量为181 m3/s；河段2长度12.15 km，20年一遇洪水流量为5 070 m3/s，平均枯水流量为181 m3/s。采用20年一遇洪水流量和平均枯水流量分别对洪水期和枯水期河道疏浚前后河道内的水位变化进行一维水力计算和二维水力计算，计算时取对应流量下电站枢纽在下游起点断面的回水水位作为下游出口控制水位，粗糙系数根据天然河流糙率表选取。

3.1" 洪水计算结果

3.1.1" 河段1

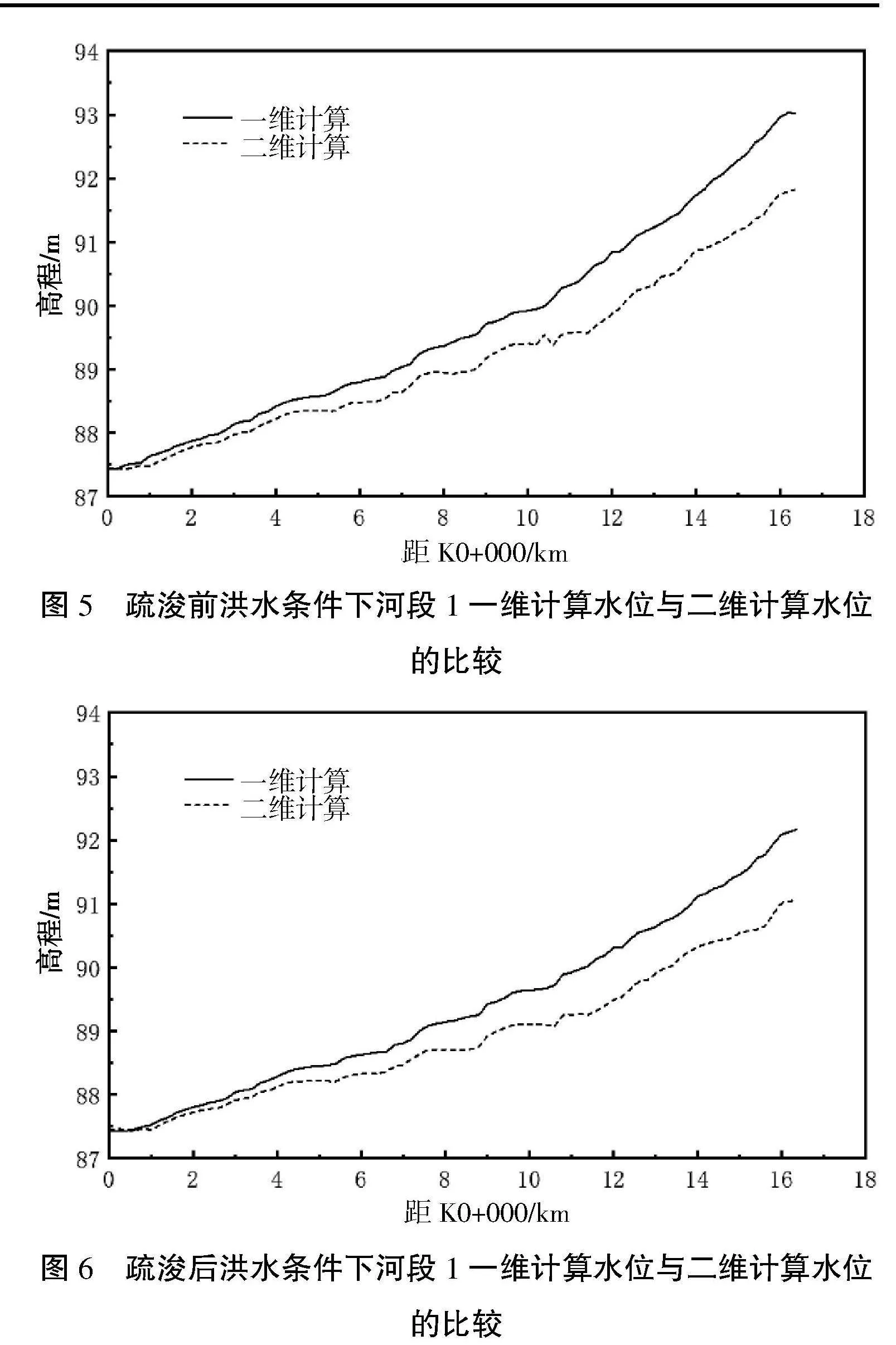
20年一遇洪水流量5 090 m3/s下，水位计算结果与一维水力计算结果的比较如图5和图6所示。本次二维计算得到的水位值与初设结果沿程变化趋势一致，但初设一维水力计算结果普遍高于本次二维模型计算结果，这主要是由于工程河段水下地形起伏较大，一维水力学计算方法不能反映地表起伏变化的影响，计算结果偏差较大处出现在模型上游边界范围附近，疏浚后工程河段水下地形起伏变化变得平缓，计算结果偏差有所减小，工程前后最大计算结果偏差分别为1.25 m和1.12 m。

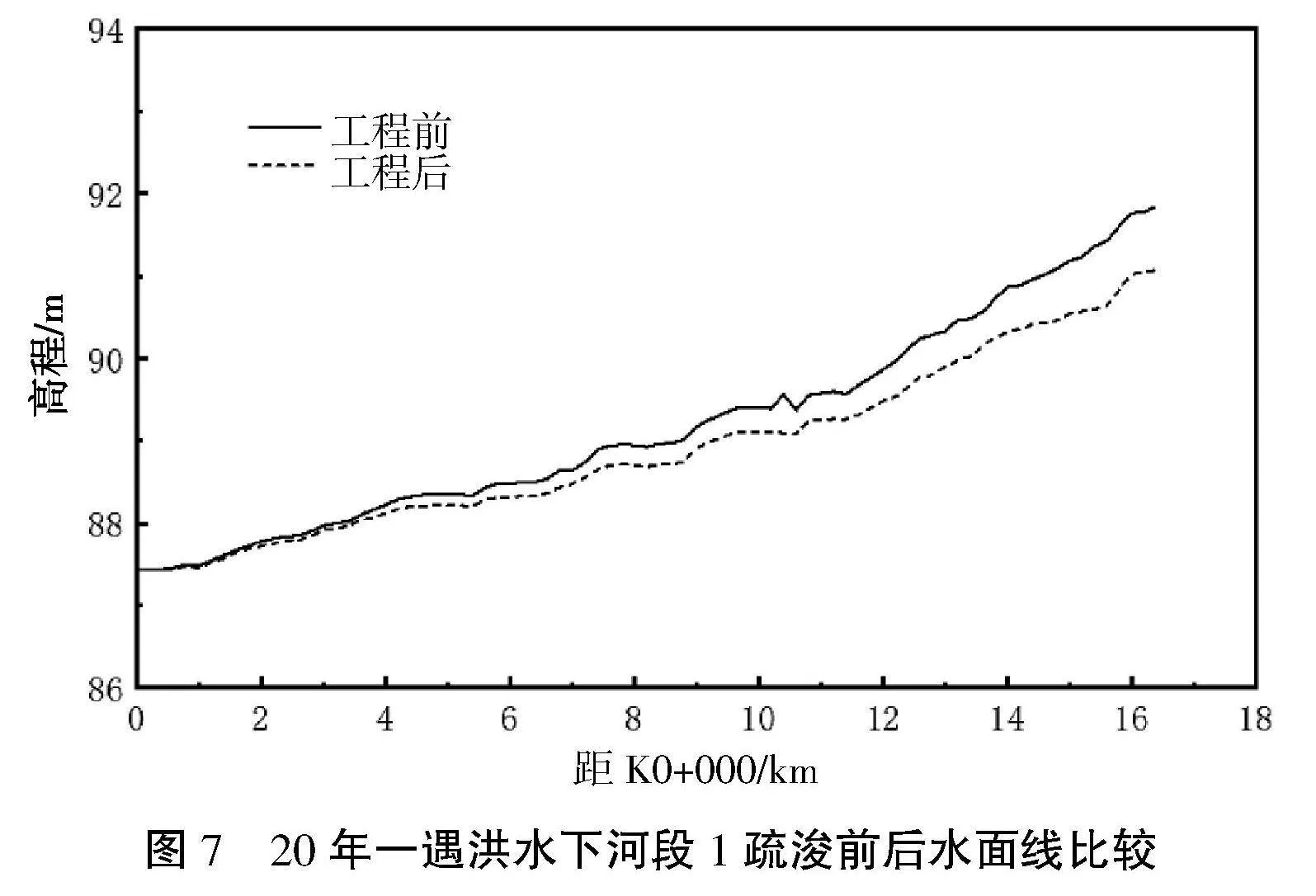
计算结果表明工程疏浚后水位值有所下降，水位下降主要发生在上游段，最大水位降幅为0.78 m，如图7所示，工程后沿程水面线变化较工程前更平缓，平均坡降0.22‰，沿程最大比降0.98‰，出现在K15+600～K15+800河段。

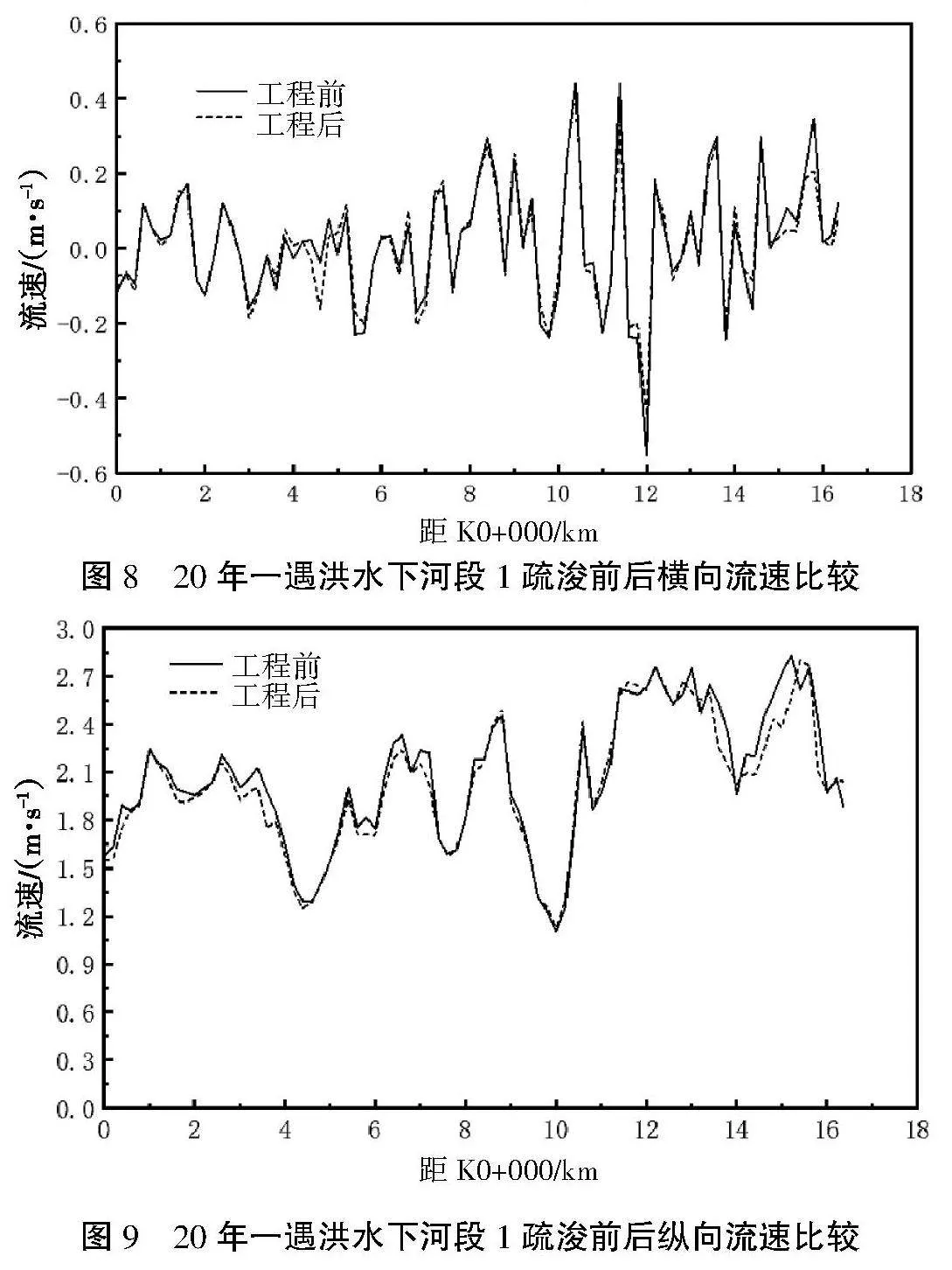
工程河段清淤疏浚后，由于扩大过水断面面积，洪水流速降低。图8和图9分别为工程前后横向流速和纵向流速的比较，可以看出，工程后横向流速和纵向流速均有所减小，但变化幅度不大，工程前沿程最大平均横向流速和最大平均纵向流速分别为0.453 m/s和2.829 m/s，工程后沿程最大平均横向流速为0.448 m/s，出现在K12+000断面，最大平均纵向流速为2.803 m/s，出现在K15+400断面。水流基本顺着航道流动，水流较平顺，沿程不同航道断面的流速分布均较均匀。

3.1.2" 河段2

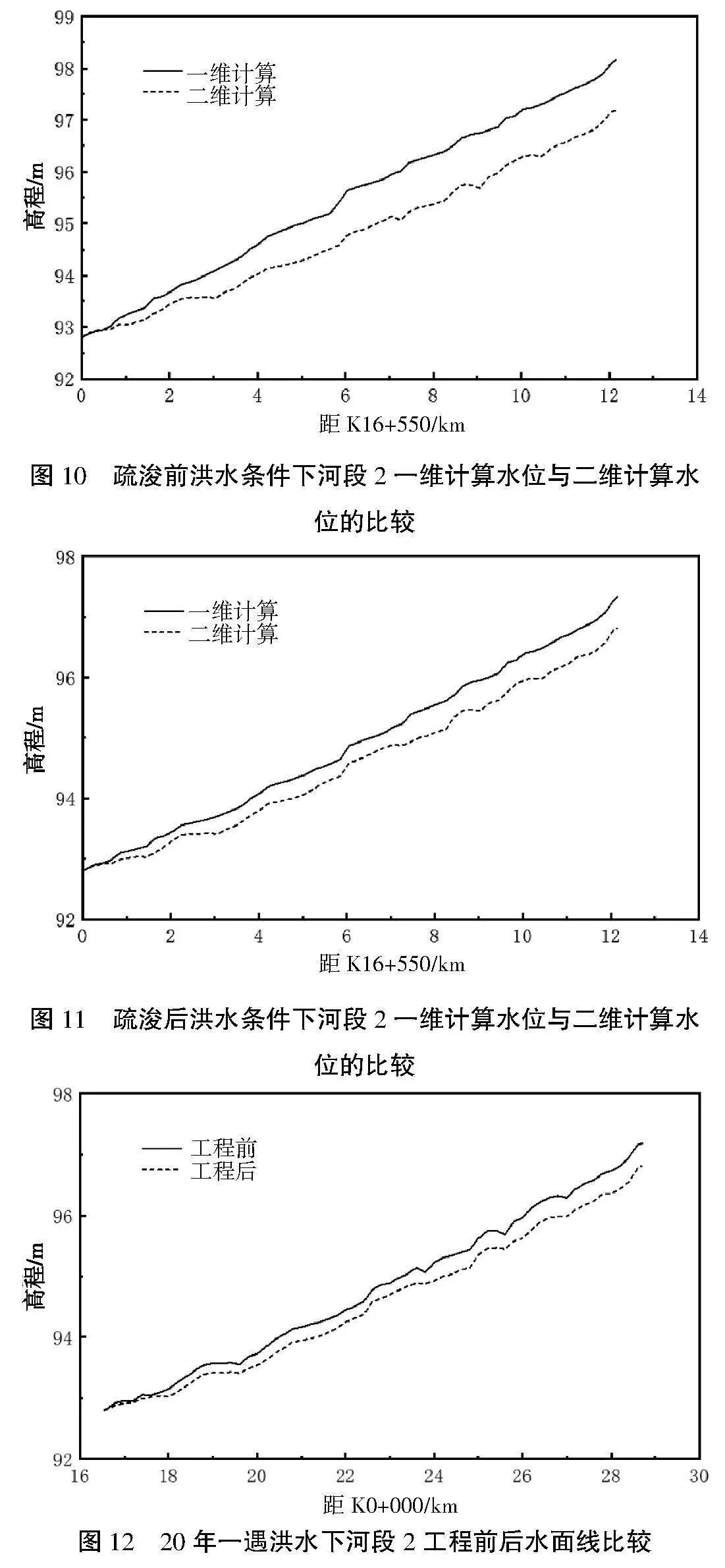
流量为20年一遇洪水流量Q=5 070 m3/s，下游水位出口水位为20年一遇洪水位92.8 m时，水位计算结果与初设一维水力计算结果的比较如图10和图11所示。与河段1的计算结果相似，初设一维水力计算结果普遍高于本次二维模型计算结果，计算结果偏差较大处出现在模型上游边界范围附近，工程后计算结果偏差小于工程前的，工程前后最大计算结果偏差分别为1.07 m和0.51 m。

计算结果表明工程疏浚后水位值有所下降，但降幅较小，最大水位降幅为0.41 m，如图12所示，工程后沿程水面线变化较工程前更平缓，平均坡降0.32‰，沿程最大比降为1.09‰，出现在K28+400～K28+600河段。

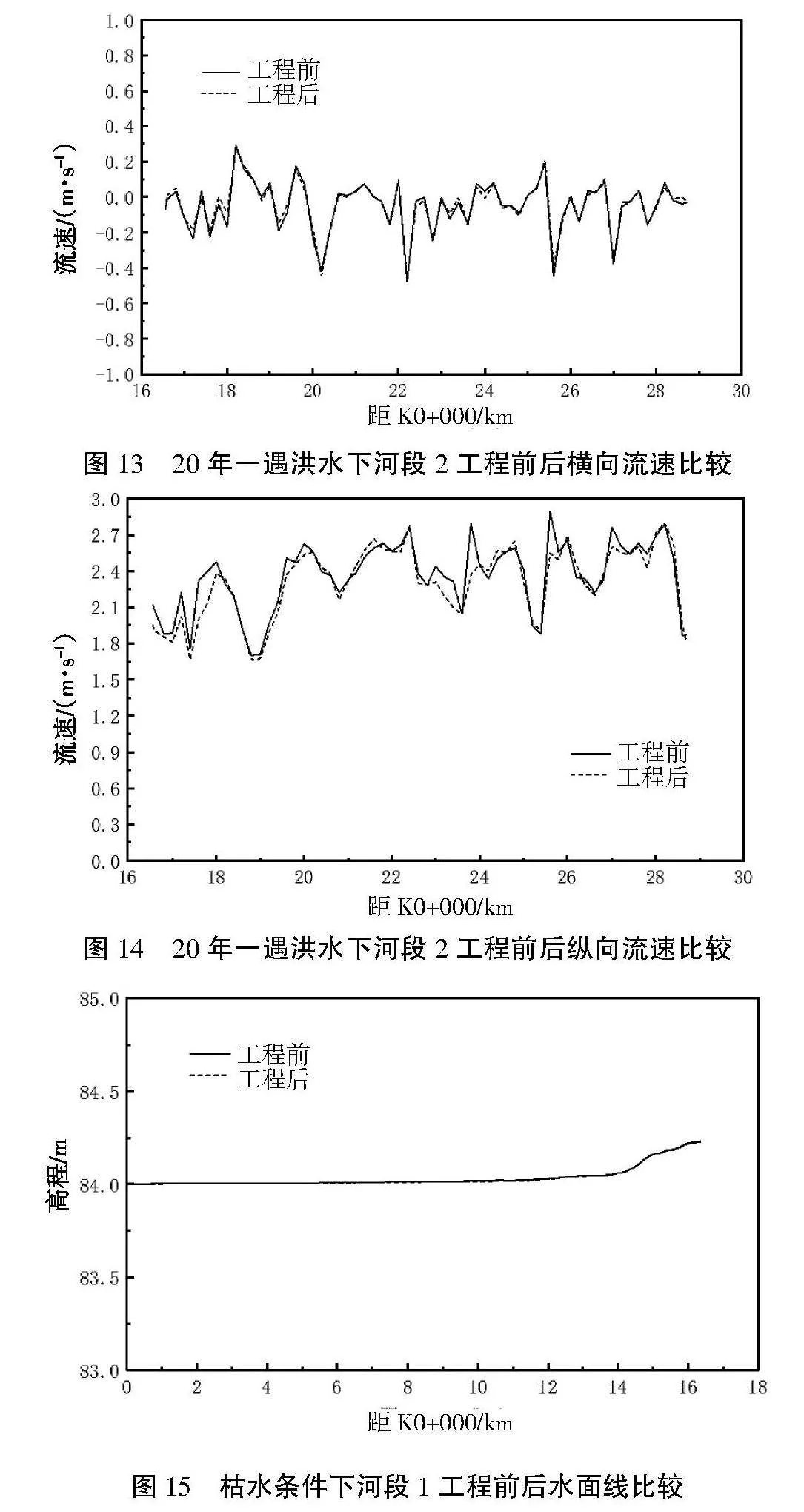
图13和图14分别为工程前后横向流速和纵向流速的比较，可以看出，工程后横向流速和纵向流速均有所减小，但变化幅度不大，工程前沿程最大平均横向流速和最大平均纵向流速分别为0.475 m/s和2.89 m/s，工程后沿程最大平均横向流速为0.465 m/s，出现在K22+200断面，最大平均纵向流速为2.772 m/s，出现在K22+400断面。

3.2" 枯水计算结果

3.2.1" 河段1

在枯水流量Q=181 m3/s，下游水位出口水位下游出口水位为耒中水电站死水位84.0 m时，上堡水电站坝下河段1工程前后如图15所示，工程疏浚后水位值有所下降，但降幅非常小，最大水位降幅为0.003 m，工程前后水面线几乎重合，比降也很小，工程后平均坡降0.014‰，沿程最大比降为0.16‰，出现在K14+600～14+800河段。上述规律与初设枯水条件下一维水力计算结果较为一致。

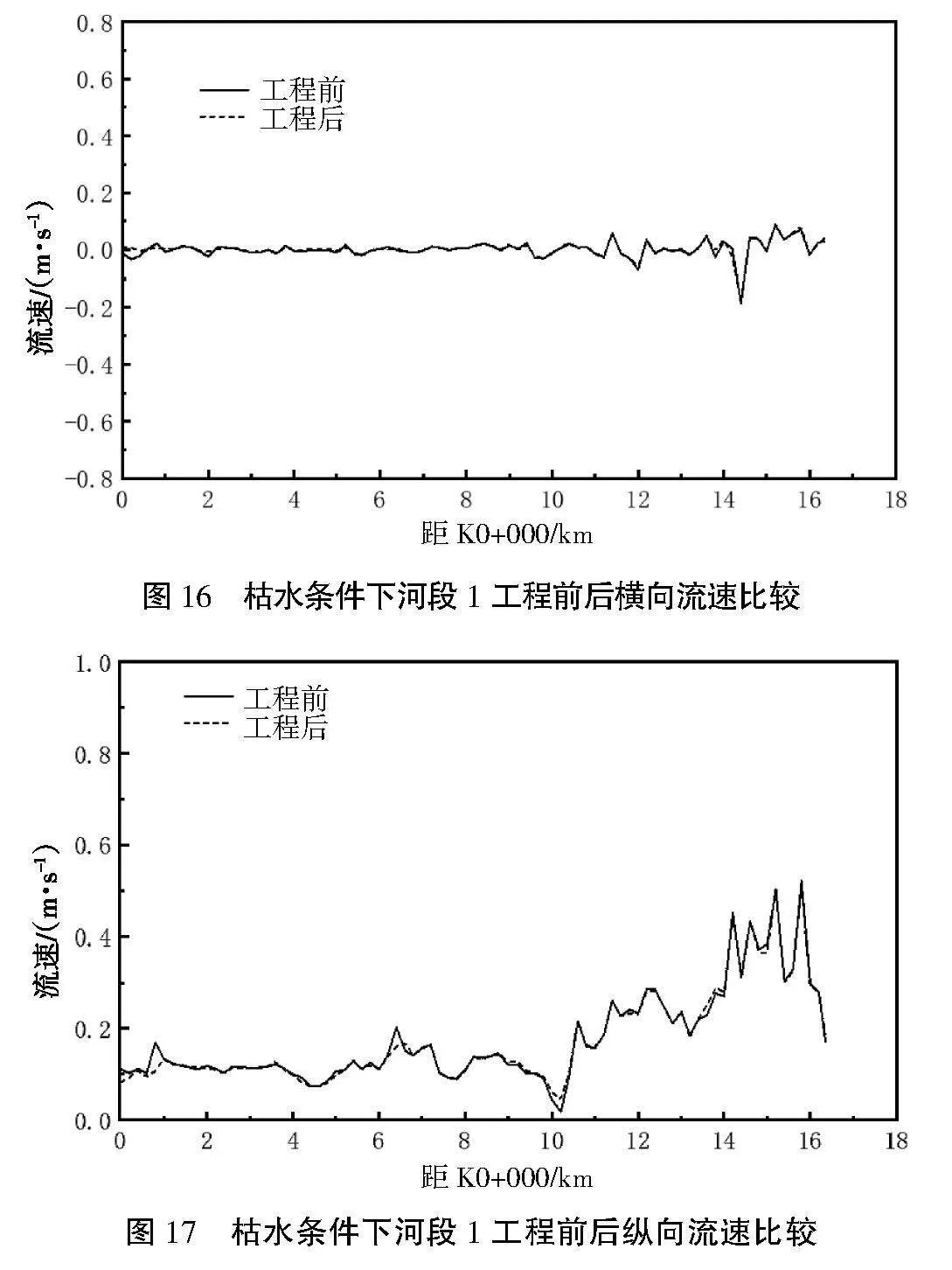
图16和图17分别为工程前后横向流速和纵向流速的比较，可以看出，工程后横向流速和纵向流速均有所减小，但变化幅度不大，工程前沿程最大平均横向流速和最大平均纵向流速分别为0.186 m/s和0.521 m/s，工程后沿程最大平均横向流速为0.177 m/s，出现在K14+400断面，最大平均纵向流速为0.51 m/s，出现在K15+800断面。水流基本顺着航道流动，水流较平顺，沿程不同航道断面的流速分布较均匀。

3.2.2" 河段2

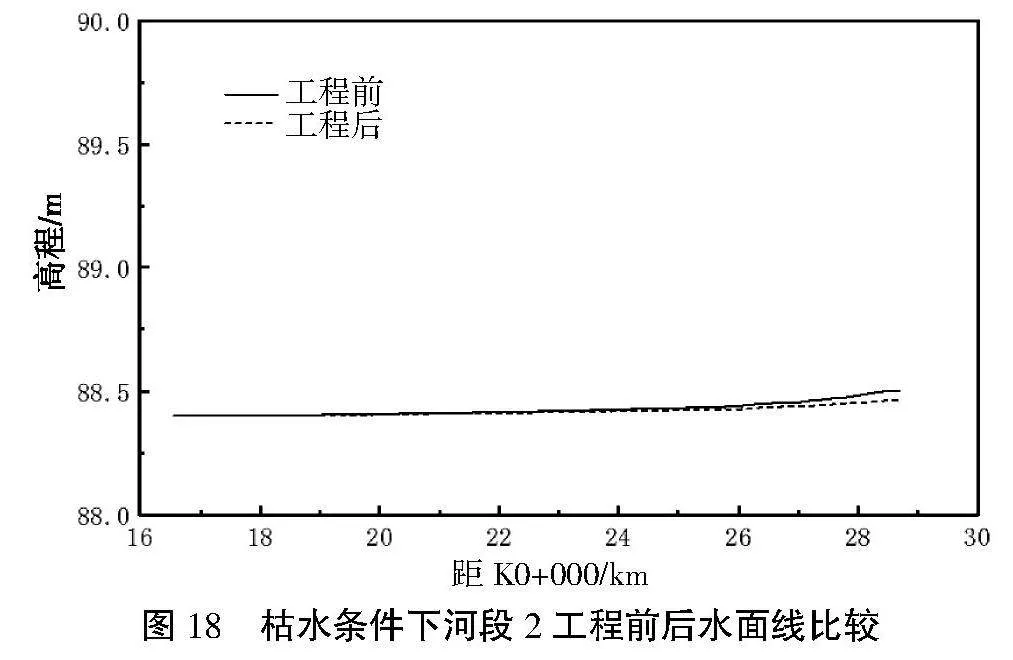
在枯水流量Q=181 m3/s，下游水位出口水位下游出口水位为耒中水电站死水位88.4 m时，水电站坝上河段2工程前后如图18所示，工程疏浚后水位值有所下降，但降幅非常小，最大水位降幅为0.039 m，工程前后比降很小，工程后平均坡降0.005‰，沿程最大比降为0.02‰。上述规律与初设枯水条件下一维水力计算结果较为一致。

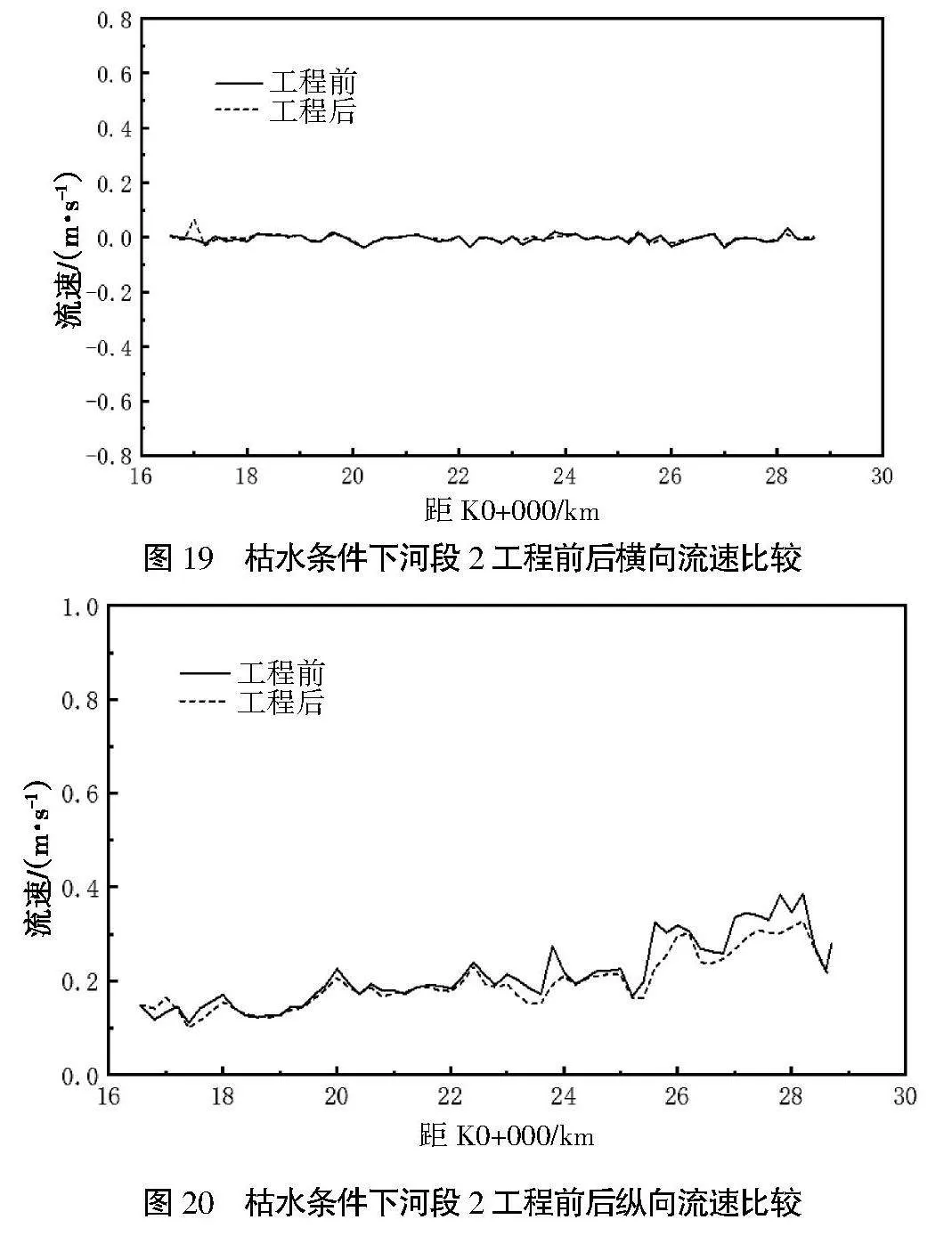
图19和图20分别为工程前后横向流速和纵向流速的比较，可以看出，工程后横向流速和纵向流速均有所减小，但变化幅度不大，工程前沿程最大平均横向流速和最大平均纵向流速分别为0.037 m/s和0.386 m/s，工程后沿程最大平均横向流速为0.067 m/s，出现在K17+000断面，最大平均纵向流速为0.327 m/s，出现在K28+200断面。水流基本顺着航道流动，水流较平顺，沿程不同航道断面的流速分布较均匀。

4" 结论

选取某山区河流的2个疏浚河段，对洪水条件下和枯水条件下的沿程水位进行了一维水力计算和二维水力计算，计算结果表明，一维水力计算和二维水力计算结果的差异与计算流量和河底地形有关，洪水条件下一维水力计算得到的水位要高于二维模型计算结果，两者的偏差依赖与河底地形的起伏变化程度，地形变化越剧烈两者的偏差也越大；枯水条件下一维水力计算得到的水位低于二维模型计算结果，两者的偏差较小。因此，对于河底地形变化平缓河段的枯水水位计算，采用一维水力模型是合适的，但对于洪水及河底地形变化剧烈的河段的水位计算将可能出现较大的误差。

工程河段的清淤疏浚扩大了河道的过水断面面积，使航道内的流速减小，水流基本顺着航道流动，水流较为平顺，沿程不同航道断面的流速分布较均匀。20年一遇洪水流量下上堡水电站下游河段1航道内最大断面平均横向流速和最大断面平均纵向流速分别为0.448 m/s和2.803 m/s，相比工程前分别减小了0.005 m/s和0.026 m/s；河段2航道内最大断面平均横向流速和最大断面平均纵向流速分别为0.465 m/s和2.772 m/s，相比工程前分别减小了0.01 m/s和0.118 m/s；工程后纵向流速均小于3 m/s；枯水条件下2个河段的横向流速和纵向流速均很小，工程前后流速变化亦很小。

参考文献：

[1] 王领元.应用MIKE对河流一、二维的数值模拟[D].大连：大连理工大学，2007.

[2] 黄惠明，施春香.一维河网水流数学模型数值计算方面的探讨[J].吉林水利，2005（9）：38-41.

[3] 马中伟，陈界仁，汪迎春.河网一维水流模型在赣江二级航道整治中的应用[J].中国水运，2015，15（5）：244-246.

[4] 李允军，徐青，周元斌，等.二维水动力学模型在蓄滞洪区洪水演进模拟分析中的应用[J].江苏水利，2018（12）：68-71.

[5] MIKE1-水动力模块中文教程[Z].2012.