笛子音准问题的解决策略：管口校正与内径调整对音准的协同影响研究

摘要：我国的笛子制作至今仍然存在音准瓶颈：传统的音孔校音方法不足以校准相同管长下的八度关系和五度关系。本文依据驻波原理，以音孔校音方法与末端“管口校正”的关系为切入口，认为末端“管口校正”就是改变管口波腹处的内径大小，而调整管内波腹与波节处内径大小对频率同样有显著影响，据此提出：挖补音孔与打磨填补管内局部内径相结合的方法是切实解决笛子音准问题的有效手段。

关键词：笛子" 管口校正" 变径规律" 内径" 驻波

我国传统的笛子是六个音孔平均排列的“匀孔笛”，自上世纪20年代起，为适应社会音乐生活的发展，“匀孔笛”逐渐演变为孔距不平均的“十二平均律笛”，并在上世纪50年代得以定型。尽管采用十二平均律的现代笛子已发展近百年，但在制作中却始终存在音准瓶颈，且常有多种“疑难杂症”难以解决。本文将探讨笛子音准问题的根本原因，分析现有校音方法的局限，并基于驻波原理提出解决方案。

一、当代笛律理论与实践中的音准问题

在当代笛律理论中，最为全面的研究当属南派笛子代表人物赵松庭于1973年发表的《横笛的频率计算与应用》①。该研究是在同济大学物理系教授赵松龄的帮助下完成的，这是笛子基于现代声学理论研究的开端。赵松庭的研究涵盖了笛子的频率计算公式、频率标准与温度标准确立、管口校正量与相关物理量的关系及计算公式等内容。这些研究结合了大量实践，至今仍被视为笛子制作的“金科玉律”。然而，赵松庭也指出，估计存在约2%的误差。后续研究者也认为赵松庭的计算公式十分复杂，且管长修正数的计算结果与实测结果存在误差，有待完善②。

北京大学力学系教授武际可于1992年发表了《怎样制作笛子》③，其中提道：“笛子制作是一个典型的力学问题，笛子从吹孔到指孔长度同发音频率的关系，应当运用力学知识加以精确化。”该文根据声速、音高频率以及管口校正量等条件，给出了常用笛子管长与开孔的计算方法，并提供了结论性数据。

上海艺术研究所研究员陈正生自上世纪80年代以来发表了60余篇与笛律相关的研究文章，涉及“管口校正”与“异径管律”等理论与制笛方法，并对赵松庭的理论及历史上的管口校正研究进行了深入评述④。

在上述研究中，管口校正量是争议的焦点，这是自晋代“荀勖笛律”以来就一直讨论的话题。近期，史凯敏、刘勇《开管管口校正与计温律高计算公式验证——基于黄钟律管的三组实验》⑤一文中就列举并评析了前人研究的10种不同的管口校正量，并通过实验得出了相关数据，尽管实验中所用律管为竖吹，但管口校正的原理与横吹的笛子是一致的。

引起管口校正量争议的原因主要有两点：一是吹口端校正量的问题，这与测试者的吹奏状态有极大关系，即使同一人吹奏同一管，力度或角度稍有偏差，测试结果相差5～10Hz也是常见的现象；二是管末端校正量的问题，这与测试的管体材料规则程度密切相关，特别是内径的变径规律，对频率有不可忽视的影响。

根据经验，制作笛子须采用头大尾小的变径管。目前，笛子的管体主要选用单节天然竹材，虽是变径管，但内径并不规则且缺乏统一的变径规律，如按照现有的理论公式来指导生产，要逐一测量每个竹材并不规则的物理量，几乎是毫无操作性可言，而影响笛子末端校正量的变径规律，长期以来也未被学者们作为重点讨论，这些均与笛子的音准有直接关联。因此，按照现有理论中的各种计算办法，是极难将笛子做准的。

在实际生产实践中，制作者通常不考虑这些复杂的理论和计算办法，开孔定位主要是根据经验总结而来的百分比公式。现行笛子各孔位的百分比公式，最早可追溯至1928年“大同乐会”郑觐文的笛制改革实践。上世纪五十年代，“大同乐会”乐器厂并入上海民族乐器一厂，郑氏父子的制笛方法通过师徒传承的方式代代相传。到八十年代，上海民族乐器一厂制笛师周林生又将其在长期实践中总结优化的制笛方法传承至盛产竹材的杭州余杭，此后该地也逐渐形成产业规模并发展成为我国最主要的笛子产地，而当时制作者主要是当地村民，精通演奏者甚少，对于律学、声学、力学等理论更难涉及，所以，简单易懂且行之有效的百分比公式自然就成为了制作者的主要依据，并沿袭至今。在生产过程中，制笛者只需要“依葫芦画瓢”，根据百分比公式为不同调的笛子制成不同的“划线板”进行定位开孔。

然而，由于天然竹材的内径大小、变径规律以及管壁厚薄等影响频率的物理量均难以完全统一，导致各调笛子在选材时只能执行弹性的标准，如内径仅以吹口处（偏大一头）的大小为依据，且允许相差大约1毫米。所以，当规格并不统一的竹材匹配固定的“划线板”，必然会导致笛子音准上的差异，在完成开孔后，对指孔进行挖补校音就成为了制笛工艺中最具有技术含量的核心工序。然而，这种传统的校音方法仍是“经验主义”，鲜有人去探讨其中的原理，同时，这种校音方法并不能解决所有的音准问题，在实践中，即便是经验丰富的制作者也常有难以解决的“疑难杂症”。

二、音孔校音的原理与局限

根据现有百分比定孔规则，实际管长的测量均是以各孔中心位置为起始的。如图1所示，从吹孔（进气端）到各指孔和基音孔（出气端）的中心之间的距离被定义为实际管长Ln（L0～L6），每个孔位的管长对应一个特定的比例值。例如，将最大实际管长L0设为基准值1，L1的实际长度则约为0.84。在挖补音孔的校音过程中，一种是直接改变Ln的挖补，通过改变实际管长，进而影响有效管长数；另一种是保持Ln不变的情况下进行的挖补，则是通过调整管长修正数来影响有效管长数，同样对频率产生影响。后者在不改变实际管长的情况下对频率进行的调整，本质上就是“管口校正”的一种应用。

笛子的进气端与出气端均与大气相通，属于典型的开管乐器，所以，“管口校正”的管口包括吹口端和实际管长的末端。影响吹口端校正量的因素主要是吹奏者的吹法以及吹奏状态，不仅因人而异，而且同一人在不同状态下吹奏也会产生差异，这是人为的不可控因素，与笛子的固有音准无关，而吹口端的吹孔大小及孔内锥度、笛塞位置等物理量影响的是笛子整体音高，通常是按照经验值进行预设。所以，挖补音孔的校音主要是针对基音孔和指孔的末端校正，即Ln（L0～L6）的末端，共有七处⑥。

笛子在发音时，可以将实际管长Ln的管内空气看作一段振动的空气柱，用指孔调节空气柱长度改变频率。但是，实际管长Ln（L0～L6）并不等于有效管长，为方便理解，我们暂将实际管长Ln（L0～L6）的末端看作近似管体截断面，当管内空气振动时，还会继续向管外辐射一段长度，即管外也有一段空气参与共振，所以，有效管长是实际管长与管外辐射长度之和，也叫理论管长。管末端所辐射的长度，就是“管口校正”的末端校正量，末端校正量越大，频率越低，反之则频率越高。笛子的末端实际分为两个出口，以L6为例，末端外参与振动的空气不仅有一部分从第六孔溢出，还有一部分在半开放式的管内向笛尾端及其他孔溢出，两部分均随距离衰减最终趋近于零。这种情况虽比末端为截断面的情况更为复杂，但其基本原理是相同的。

由此，在不改变实际管长Ln的情况下，末端处可影响频率的物理量则主要是内径的截断面积大小。在吹奏者提供的能量恒定的前提下，当末端处截断面积增大时，压强相应减小，此时管内振动空气辐射出管口外的长度变短，频率升高；反之，当末端处截断面积减小时，压强则相应增大，此时管内振动空气辐射出管口外的长度变长，频率降低。这就是末端处内径大小与频率的关系。

因此，在笛子每个指孔上进行挖补校音，除了直接改变实际管长之外，向其他方向的挖补，包括对指孔内侧锥度的调整，实际上就相当于改变末端处的内径大小，以此改变末端校正量来影响频率。凭借这种挖补音孔的校音方法，可以校正基频之间或相同倍频之间的音程关系，也可以校正一部分基频与倍频之间的八度关系，但不能解决由变径规律异常或管内局部不规则等因素导致的相同管长下的八度关系（基频与二倍频、四倍频）和五度关系（二倍频与三倍频）偏差，这种由天然材料个性化与不规则性等先天缺陷导致的问题，只能通过改造管内径的办法予以解决。然而，这种与频率息息相关的内径变化规律，却鲜有人关注，至今仍以模糊的概念存在于经验之中，并无定论。这就是音孔校音的局限，也是“管口校正”的局限。

三、内径校音的原理与方法

目前，在制笛过程中对管体的改造通常只涉及矫直工艺，内径的问题仍未引起足够重视。要解决笛子的音准问题，在不考虑其他替代材料和其他替代加工方式的前提下，校音的方法除了挖补音孔，还必须结合打磨或填补内径的方法。

在以天然竹材制作的同类乐器中，采用挖补音孔和打磨填补内径相结合的方法来校音的典型代表当属日本尺八⑦。改造内径是每一个尺八制作者必须掌握的技能，这种方法不仅可以校音，还可以改善音色与音量。日本尺八制作者在长期的制作过程中总结出了内径的标准数据，包括不同部位内径变化对音准、音色和音量的影响规律。不同调的尺八，其内径的变化规律基本接近，即使不同的制作者略有差异，但也仅是体现在音色或音量上，以彰显制作者的个性特点，对音准并无影响。

由于尺八与笛、箫的发声原理一致，因此，这种改造内径的工艺和数据规律对于笛、箫的制作是具有参考价值的。我国台湾省少数制箫者于早些年掌握了这个窍门，并广泛用于南箫制作，解决了箫的音准问题，并丰富了箫的音色表现。后传入大陆地区，仍主要用于制箫，同时也启发了少数制笛者。但这道工艺只能依靠手工完成，且复杂繁琐，费时费力，与笛子庞大的市场需求存在难以调和的矛盾，所以，真正研究其中原理并熟练运用者仍是凤毛麟角。

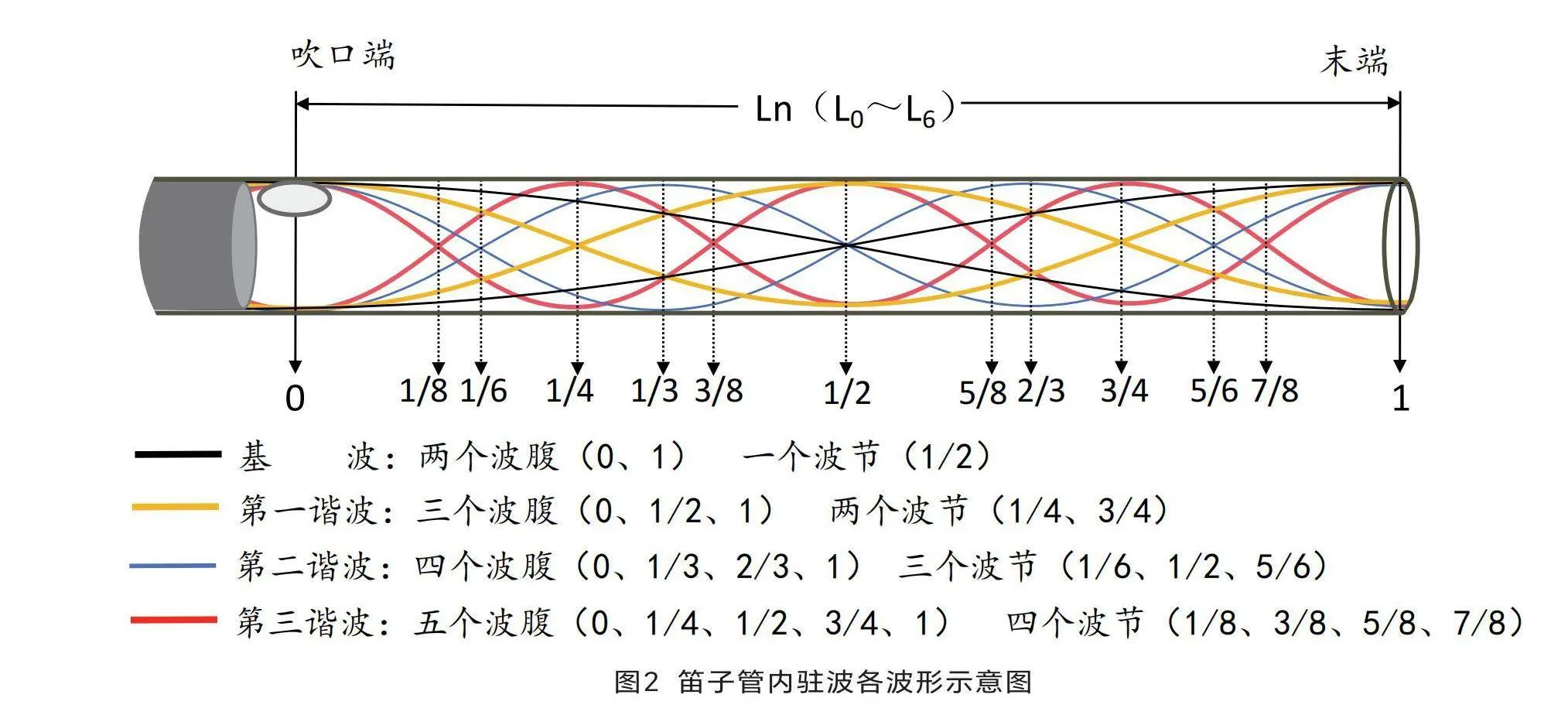
这种打磨或填补局部内径的校音方法，本质上是基于驻波原理⑧。如图2所示，由于笛子是开管乐器，不论是发基频音还是各倍频音，位于吹口端与管末端的管口均为波腹，前文所讨论的不改变实际管长的挖补音孔，则相当于改变了管末端波腹处的内径大小。波腹处内径扩大，频率升高；波腹处内径缩小，则频率降低。如采用同样的方法对管内的波腹处内径大小进行调整，对频率高低的影响一致，而对管内波节处内径大小进行调整，对频率高低的影响则相反，且实践证明有效。因此，末端校正量可以“管口校正”，也可以通过“管内”的调整来实现，二者可以相互作用，相互补偿。

按图2所示比例，与图1中各孔位置比对便可测得影响Ln（L0～L6）基频与二、三、四倍频的基波与谐波的各个波腹、波节在笛子上的位置，但处理的具体位置还要兼顾实际情况。

Ln（L0～L6）的末端共有七处，分别对应基音孔和六个不同的指孔，第五孔大约位于最大管长L0的1/2处，从此处至管末端涉及多个指孔，处理这一段内径时，很难避免顾此失彼的问题。同时，由于笛子的有效管体普遍为单节竹材，更加粗长的曲笛内径通常从膜孔附近到尾端才形成有规律的锥状递减，而膜孔向吹孔端一段的内径则由于靠近竹节而普遍呈不规则的收缩形态，这种不规则的变径规律则是造成音准“疑难杂症”的主因之一，这也是许多制作者将膜孔与第六孔之间的金属调音接口移至吹孔与膜孔之间的原因所在。因此，在进行管内波腹或波节位置的打磨或填补时，通常只针对吹口端至1/2处的区域进行操作。

由于管内波腹、波节位置交错重叠，按照波腹、波节对频率的影响规律，处理内径时还可能引发同一音孔上的八度或五度关系的新的不平衡问题。为了最大程度规避新问题的出现，笔者和杭州竹笛行业协会会长董雪华、常德羿鑫乐器有限公司制笛师刘勇分别对各不同调的笛子进行了内径调整实验，并总结出以下操作规律：调整整体音高处理0处（吹孔），调整基频处理1处（基音孔、指孔），调整二倍频处理1/2处或1/4处，调整三倍频处理1/3处或1/6处，调整四倍频处理1/4处或3/8处。实验结果表明，通过精确地打磨和填补内径，能够显著改善笛子的音准问题，尤其是那些难以通过挖补音孔解决的“疑难杂症”。更为重要的是，当基频与各个倍频的关系调整准确后，可以有效提升笛子的共鸣，和谐的基音和泛音关系还能使笛子的音色变得更加圆润丰满，对笛子整体的演奏性能有明显的改善效果。

目前，由于成本、效率和技术门槛等多方面的因素，在笛子制作中应用此方法者甚少，尚无公认的内径数据可供参考，所以，尝试研究此方法的制作者应先学习其中原理再进行实践，并不断总结经验数据来提高效率。

结语

笛子从匀孔笛演变为十二平均律笛，已有近百年历史，但音准问题仍然存在，也成了一个老生常谈的话题。从理论上来说，各调笛子的物理量都应有最理想的标准数据，如内径大小、变径规律、管壁厚度、音孔的形状、大小、位置以及孔内锥度等，然而，针对天然竹材，相关物理量标准只能划定一个弹性的概数范围，再通过挖补音孔校音来缩小其中误差，但这种单纯的末端“管口校正”并不足以解决所有的音准问题，仍存在一些相同管长下的八度关系和五度关系无法校准的情况。根据驻波原理，末端“管口校正”实际上是通过改变末端波腹处的内径大小来调节频率，将这种方法用于管内，对处于管内波腹和波节处的局部内径进行打磨或填补，即可打破传统校音手段的局限，解决音准上的“疑难杂症”，并能同步改善音色和演奏性能。

注释：

①赵松庭.横笛的频率计算与应用[J].乐器科技简讯，1973，（02）：28-42.

②张濛园，王治国.含有侧孔阵列圆柱管的发声频谱[J].声学学报，2020，45（04）：579.

③武际可.怎样制作笛子[J].力学与实践，1992，（06）：70-71.

④陈正生.我国历代管口校正研究述评[J].交响.西安音乐学院学报，1997（03）：19-22.

⑤史凯敏，刘勇.开管管口校正数与计温律高计算公式验证——基于黄钟律管的三组实验[J].中国音乐学，2022（03）：25-35.

⑥本文讨论均以六孔笛为例，常用笛子中包括的G调低音有七孔，则应增加一处末端，也是同理。

⑦尺八源自我国，唐代传入日本，并发展成为日本的主要传统吹管乐器。我国的尺八在宋代之后失传。

⑧武际可.音乐中的科学[M].北京：高等教育出版社，2012，（06）：87.