基于改进A*算法的路径规划研究

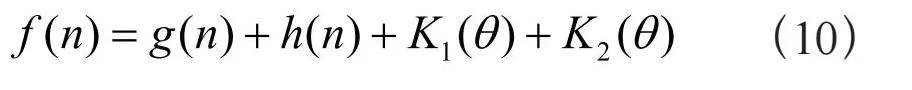
摘" 要：研究了A*算法在二、三维模型路径规划中的优化方法。通过实时阈值法和惩罚因子法减少开放列表中不必要的搜索空间和冗余路径；采用自定义优先级队列、二叉堆法和哈希表替代传统A*算法中的处理方式；在对二维地图的研究中，采用局部A*算法避免大面积搜索。实验结果表明，经过改进的A*算法显著提高了搜索和路径规划速度，减少了计算时间和内存消耗，验证了该算法的可行性和有效性。

关键词：路径规划；三维规划；惩罚因子；二叉堆与自定义优先级队列；实时阈值；局部A*算法

中图分类号：TP18；TP242 文献标识码：A 文章编号：2096-4706（2024）10-0051-06

Research on Path Planning Based on Improved A* Algorithm

CAI Zifeng， ZHANG Yansheng， LIANG Xianzhang， LUO Shihao

（Zhuhai College of Science and Technology， Zhuhai" 519040， China）

Abstract： It studies the optimization method of A* algorithm in path planning of 2D and 2D models. Reduce unnecessary search space and redundant paths in open lists through real-time threshold method and penalty factor method. Adopting custom priority queues， binary heap methods， and hash tables to replace the processing methods in traditional A* algorithms. In the study of 2D maps， local A* algorithm is used to avoid large-scale searches. The experimental results show that the improved A* algorithm significantly improves the speed of search and path planning， reduces computational time and memory consumption， and verifies the feasibility and effectiveness of the algorithm.

Keywords： path planning; 3D planning; penalty factor; binary heap and custom priority queue; real-time threshold; local A* algorithm

0" 引" 言

路径规划是移动机器人实现自主导航的关键技术之一。路径规划是指在有障碍物的环境中，按照一定的评价标准（如距离、时间、代价等）寻找到一条从起始点到目标点的无碰撞路径[1-4]。经实验验证发现，传统的A*算法[5，6]在二维和三维模型中生成的路径存在多个拐点问题，路径规划所需时间较长，对移动机器人的性能和安全性产生负面影响。复杂的路径规划可能导致机器人在应对环境变化时响应速度较慢，增加过多的转弯操作可能带来误差并加剧机器人硬件的磨损。此外，过多的拐角可能造成视野盲点，增加潜在风险。

针对这些规划时间过长、效率低下等问题，常用的路径规划算法人工势场法、模糊逻辑算法、自由空间法、遗传算法等[7，8]在解决路径规划问题方面表现出优势，但计算效率仍有其他的较好的优化方式。为了改善算法的计算效率和路径优化问题，本文采用栅格法构建环境模型，从两个方面来优化A*算法：从性能优化的角度，采用实时阈值法、二叉堆与自定义优先级队列优化，引入哈希表、局部A*算法；从路径优化的角度，通过设计惩罚因子来减少路径拐点数，算法会更偏向于走直线路段，进一步优化生成的路径。

1" 模型建立

1.1" 二维模型建立

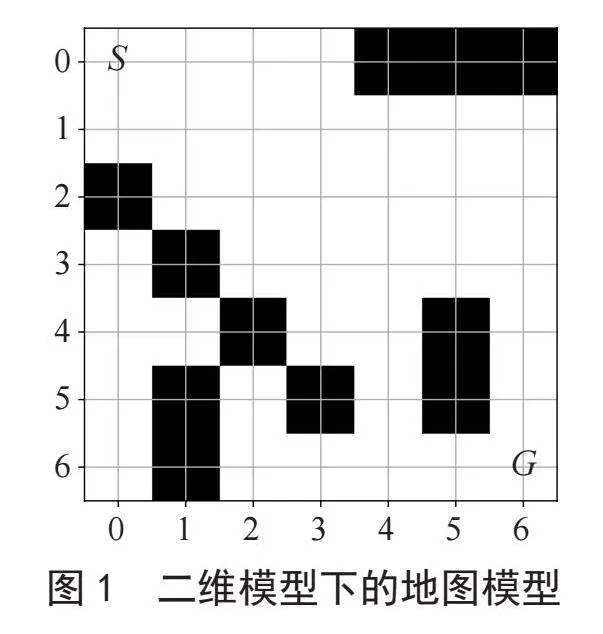
在二维地图模型的研究中，构建一个n行m列的栅格地图。其中，空白栅格表示可行走区域，而黑色栅格代表障碍物，即无法穿越的区域。研究仅考虑机器人在上下左右4个正方向上的移动，不涉及对角线或其他方向的移动。图1展示了一个7×7大小的栅格地图，起点为S（0，0），终点为G（4，4）。

1.2" 三维模型

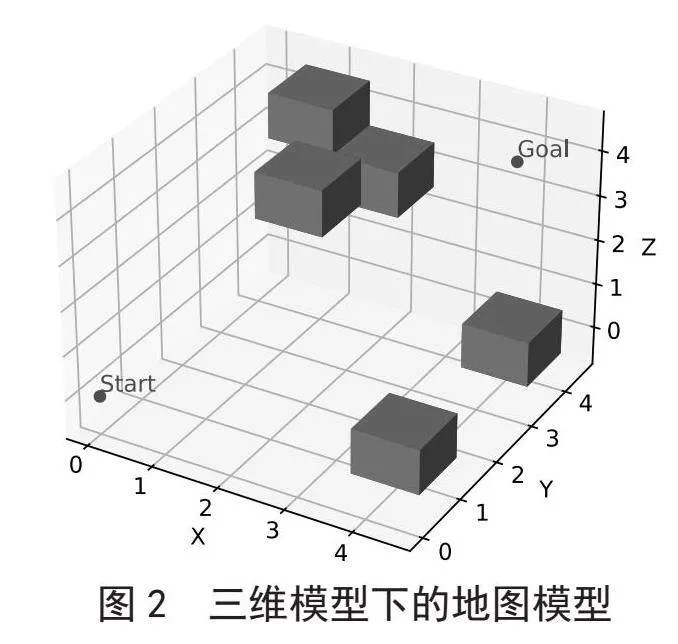
如图2所示，构建了一个大小为5×5×5的三维空间，其中黑色区块表示障碍物的位置，起点（0，0，0）终点（4，4，4）。

2" A*算法的性能优化

2.1" 实时阈值

在图1中，使用曼哈顿距离作为启发式函数，代表从当前位置到目标点水平和垂直移动所需的步数。最大曼哈顿距离为14步（例如从S到G），设置启发式值的阈值为14，在A*搜索中超过阈值的格子将被滤除，滤除的节点将不会参与下一步的计算中。曼哈顿距离公式为：

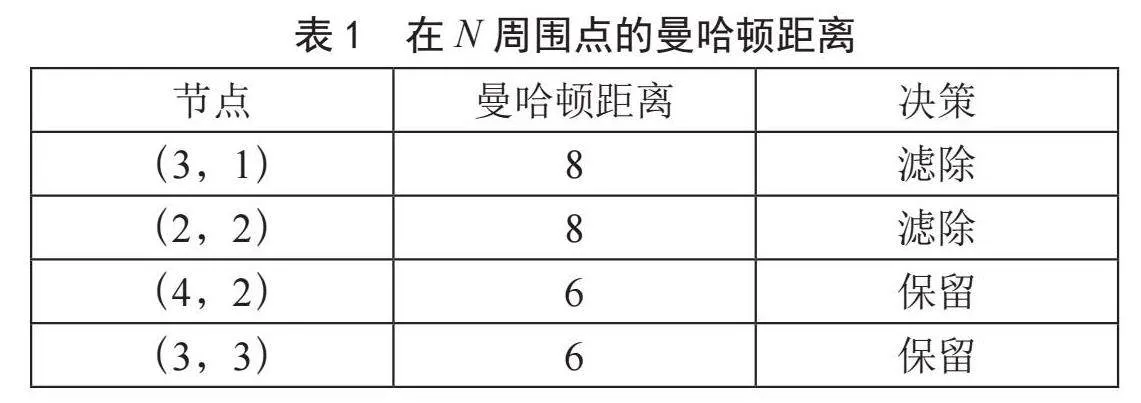
再例如，假设机器人已经移动到点（2，3），此时的曼哈顿距离为d1 = 7。因此，实时阈值将设为7。在算法推进中，计算出（3，1）和（2，2）两点的曼哈顿距离均大于阈值，那么直接忽略这两个节点，如表1所示。

在二维模型中，当启发式值大于等于某一阈值时，节点将从开放列表中滤除，以节省计算资源。在三维模型中，采用三维模型下的曼哈顿距离式（2）计算周围点的值，即可达到相同的效果。这种策略特别适用于启发式函数能够快速确定无前景路径的情况。

2.2" 自定义优先级队列与二叉堆优化

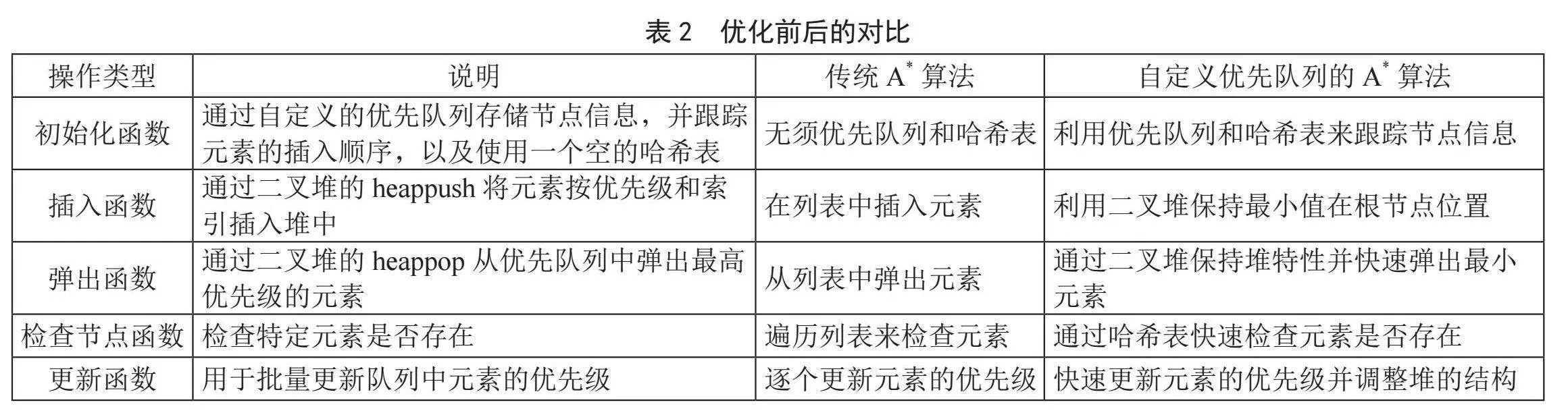
对于传统的A*算法，随着算法推进，需要管理大量节点数据，导致时间复杂度增加，计算效率降低。为了优化这一问题，可以通过建立一个自定义的优先级队列PriorityQueue来改进传统的A*算法。这个自定义的优先队列基于Python中的堆实现，同时利用哈希表来快速进行元素查找操作，避免了对整个列表的遍历来查找特定元素。通过表2来呈现优化前后A*算法的对比。

2.2.1" 二叉堆优化

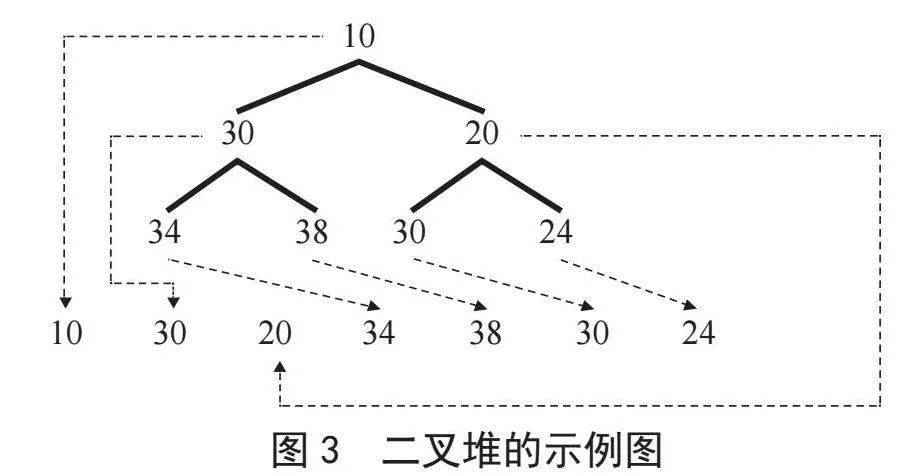
二叉堆被视为一种特殊的堆数据结构，其结构类似于完全二叉树。其满足堆的重要特性：父节点的值始终小于或等于（或者大于或等于）任何一个子节点的值。

如图3所示[9]，在给定的二叉堆中，假设节点的值表示了A*算法中的F值。最小的F值节点10位于堆的顶部，其次是20作为其子节点。第三小的节点是24，距离堆顶有两步的距离。尽管它小于30，但30位于第二层左侧，距离堆顶只有一步距离。实际上，仅需满足每个单独子节点的值都比其父节点大或相等的条件即可，其他节点在堆中的位置并不影响这一性质。这种特性使得二叉堆成为一种高效的数据结构，能够在A*算法中快速找到最小的节点。

2.2.2" 哈希表

当引入哈希表用于A*算法时，其中节点的状态作为键，与该节点相关的信息（如代价、路径等）作为值。

哈希函数将节点的状态映射到存储桶的位置，其中NodeState是节点状态的集合，Indices是存储桶的索引集合[10]。通常可以表示为：

存储桶仍然代表哈希表的存储位置，每个存储桶包含一个链表，其中存储的是与特定状态相关的信息，如代价和路径：

当需要查找节点时，通过哈希函数找到节点状态对应的存储桶位置i，在存储桶的链表中搜索节点信息。同理，当需要将新的节点信息插入哈希表时，通过哈希函数找到存储桶的位置i。

搜索操作：

插入操作：

2.3" 局部A*算法

针对大规模二维地图的问题，无论是经过优化的A*算法还是传统A*算法都需要处理大量候选节点，从而导致搜索的时间复杂度增加。因此，提出了一种针对大型二维地图的局部A*算法思路。该方法的主要目标是根据当前节点的位置为中心（xs，ys），裁剪出一块可自定义边长rs的区域作为子地图（x s- rs，ys - rs） （xs + rs，ys + rs），如图4所示，深灰色区域为D1点的子地图。这样算法不再需要处理大量的节点，只需对当前所在子地图进行计算即可。同时，启发式函数被修改为当前节点到最终目标点的曼哈顿距离，以更好地适应局部搜索的特点。

将子地图定义为（left，right，top，bottom），子地图划分计算：

确保了子地图边界不会超出地图的合法范围。

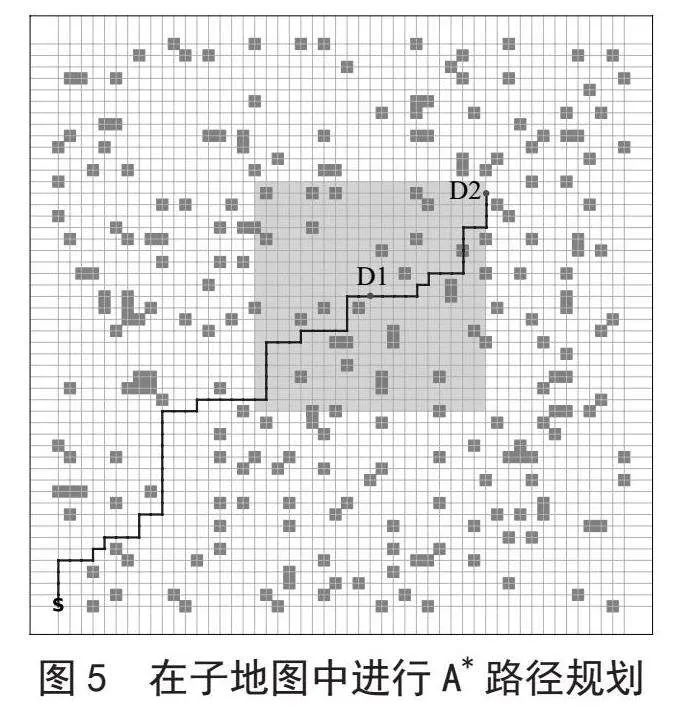
为了展示该方法的有效性，构建一个50×50的二维地图，并设置起点为（0，0），终点为（49，49）。根据当前点D1的位置，重新修改起始坐标并进行应用A*算法得到D1到D2点为路径，如图5所示。

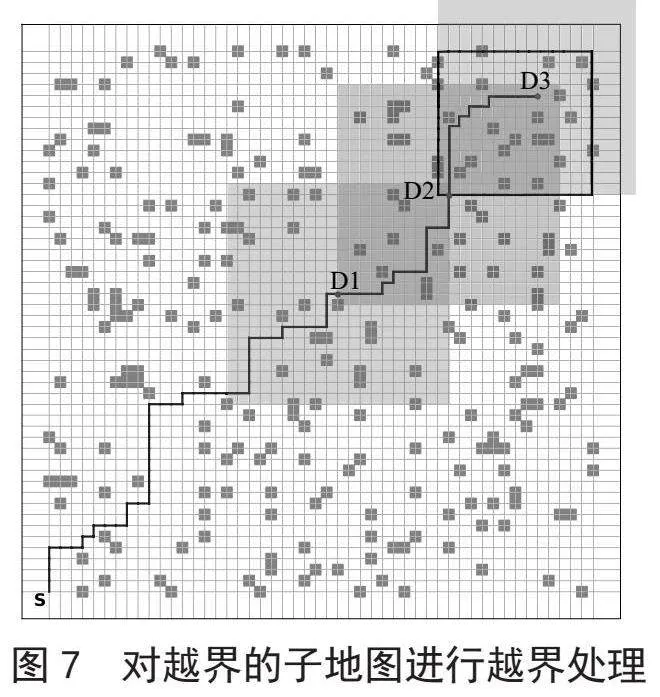
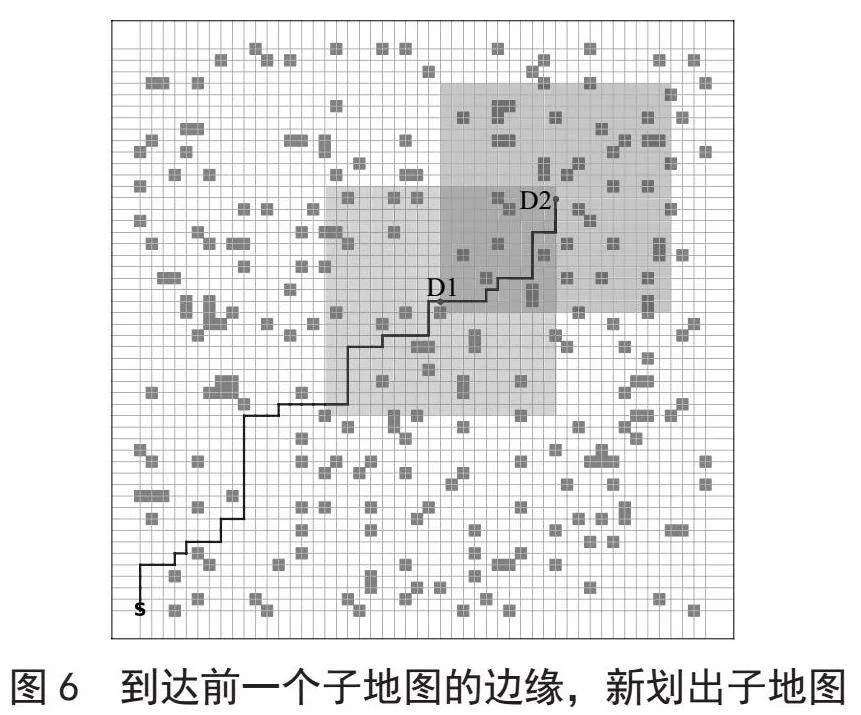
当到达子地图边界时，当前节点D2坐标以其为中心划出新的子地图，如图6所示。当划出的区域超出大地图时，会做出越界处理灵活改变子地图的大小，如图7所示，黑色框为灵活变化后的实际子地图。

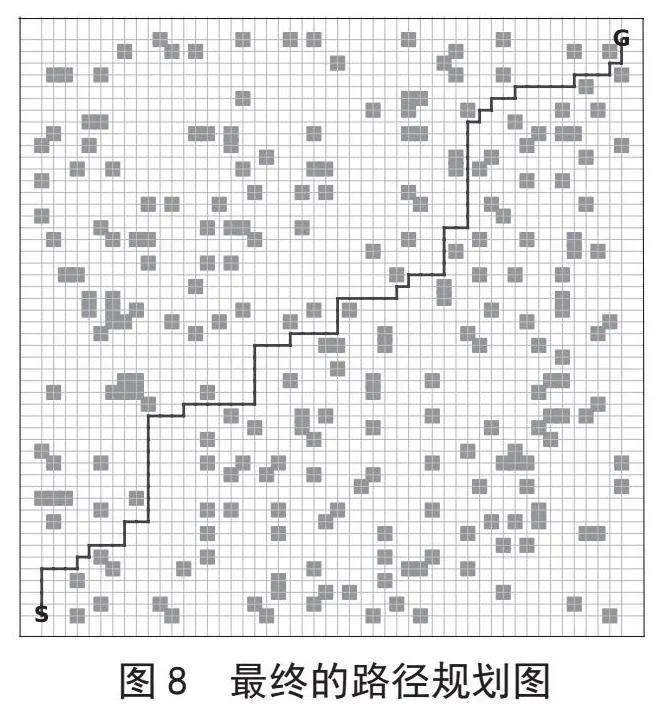
如图8所示，将所有小地图的路径拼接在一起得到最终的路径。局部的A*算法有效地减少了对大量节点的管理和搜索，从而降低了计算复杂度，提高了搜索效率，并优化了资源利用。

3nbsp; A*算法的路径优化

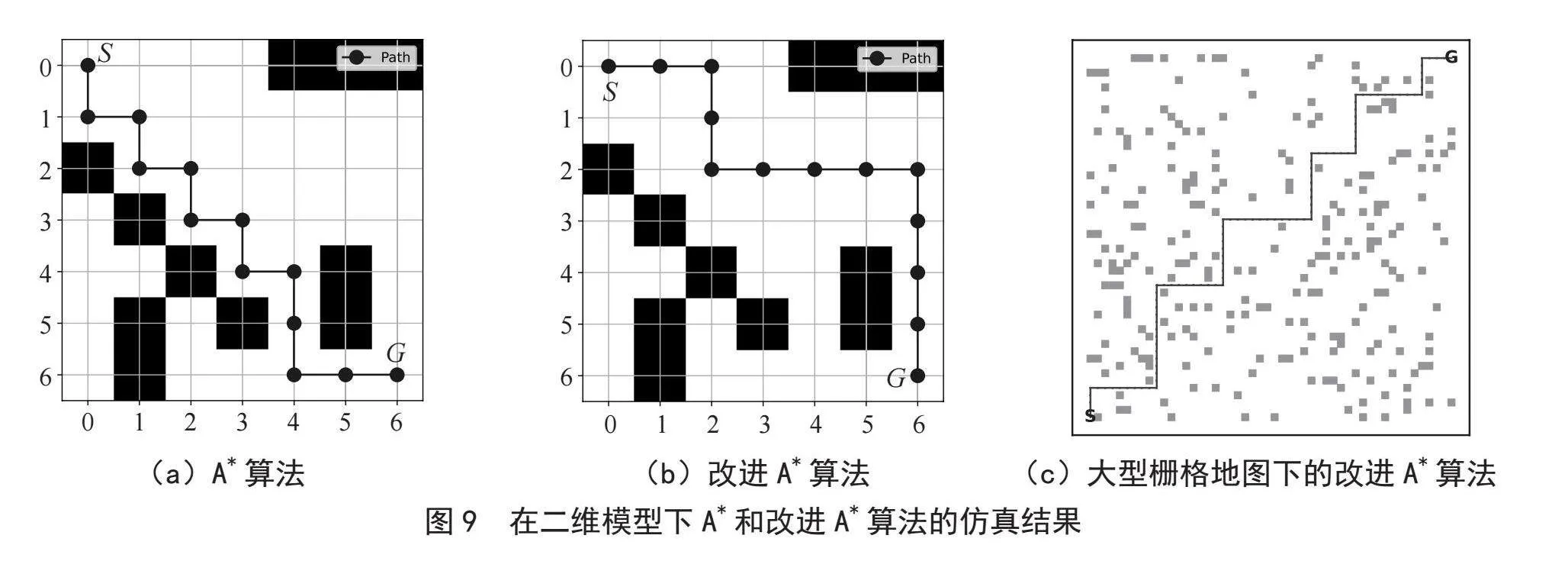
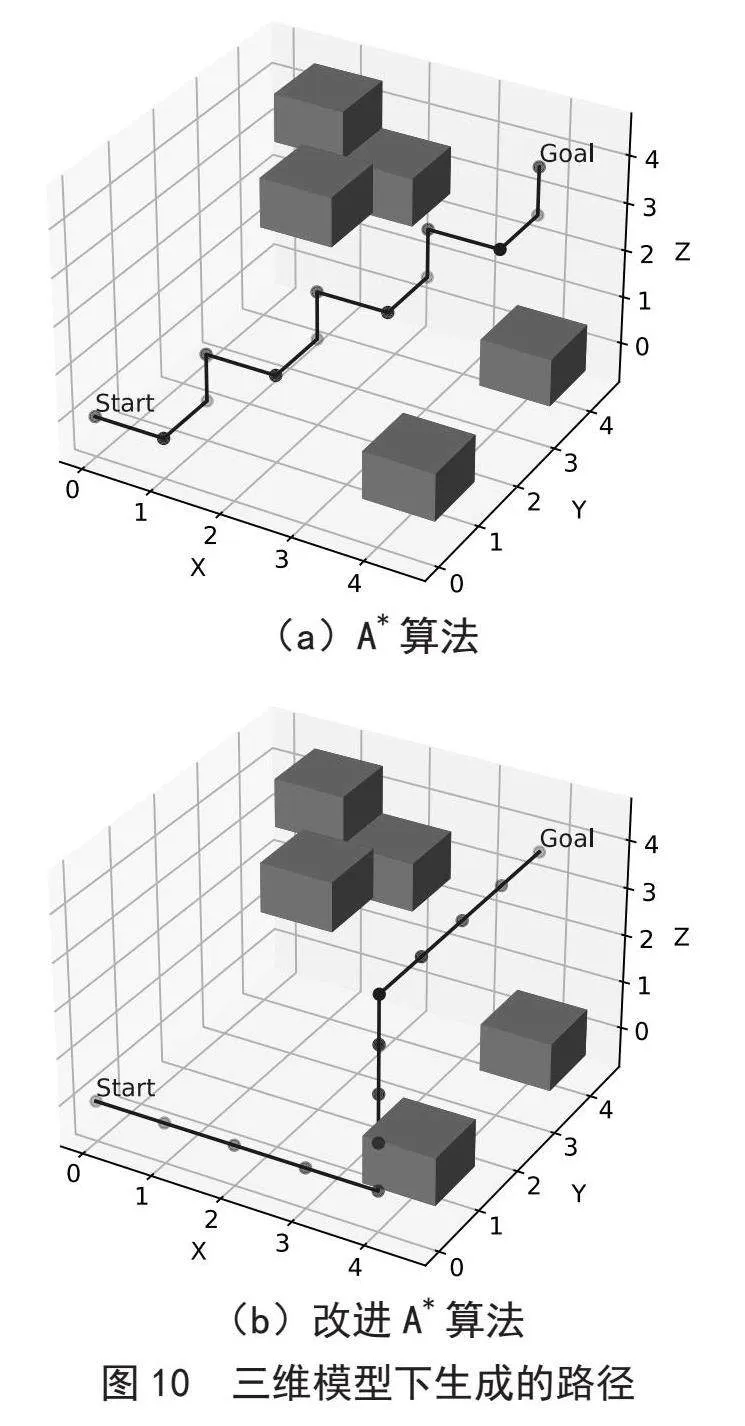
在复杂环境中，由于路径中可能存在大量拐点，导致算法效率降低。图8、图9（a）和图10（a）展示了二维模型和三维模型中传统算法输出路径，其拐点数量显著。

3.1" 二维模型

为解决该问题，引入节点惩罚因子成为改进A*算法路径选择的一项策略。通过添加拐点惩罚因子，算法更倾向于选择直线路径而非频繁转向的路径，从而减少拐弯次数，提高路径规划效率。

引入父节点P，即当前节点的前一个节点，假设父节点P为（xp，yp），当前节点C为（xc，yc）。

3.1.1" 计算转向角度

1）计算当前节点C到父节点P的向量和到相邻节点N的向量：

2）计算向量的点积d和长度l：

3）计算余弦值：

4）进行范围修正：

如果余弦值cosθ＞1.0，则设置cosθ = 1.0。

如果余弦值cosθ＜-1.0，则设置cosθ = -1.0。

5）计算转向角度：

3.1.2" 计算转向惩罚因子

由上一节得到转向角度θ，假设转向惩罚因子为K（θ）。假设θ的取值范围是从0到360度（0到2π弧度），K（θ）的取值范围是从0到1。

其中，m和b是线性函数的斜率和截距，用于将转向角度映射到转向惩罚因子的范围内。为了满足条件：

可以确定m和b的值。得到以下两个方程：

因此得到b = 0；k = 1/360；最后得到的线性函数可以表示为：

最后融入f （n）式子中为：

3.2" 三维模型

在三维模型中，可以采用相同的方法计算转向角度和转向惩罚因子，确保计算的角度适用于三维空间，并将角度值代入相同的线性函数中计算转向惩罚因子。这种转向惩罚因子的计算仍然遵循相同的线性函数，只需在三维空间中应用。可以将三维模型分解为z-x和x-y或其他两个二维模型组合，通过计算转向角度和转向惩罚因子的方法得到K1（θ）与K2（θ），最后融入三维模型中的f （n）中：

4" 实验仿真

为验证改进的A*算法的有效性，在二维和三维模型下分别针对A*算法和融合了实时阈值、二叉堆与优先级队列、惩罚因子的改进A*算法进行仿真实验。实验将在5个不同尺寸的栅格地图中展开，以全面评估算法在不同场景下的性能表现和适用性。

4.1" 优化路径实验仿真

图9（a）所示的7×7栅格地图下进行了A*算法的仿真实验。其中，S代表起始节点，G代表目标节点，黑色栅格表示障碍物，而蓝色线段展示了经过A*算法生成的最终路径。在实验中，通过引入惩罚因子，进一步优化了路径的生成，如图9（b）所示。此外，在50×50的大型栅格地图中同理，如图9（c）所示，相比之前的实验结果（图8），得到了路径规划方面的优化效果。

图10（a）表示在图2所建立的三维栅格地图中进行A*算法的仿真实验，通过引入三维下的惩罚因子，得到优化的三维路径，如图10（b）所示。

4.2" 优化性能实验仿真

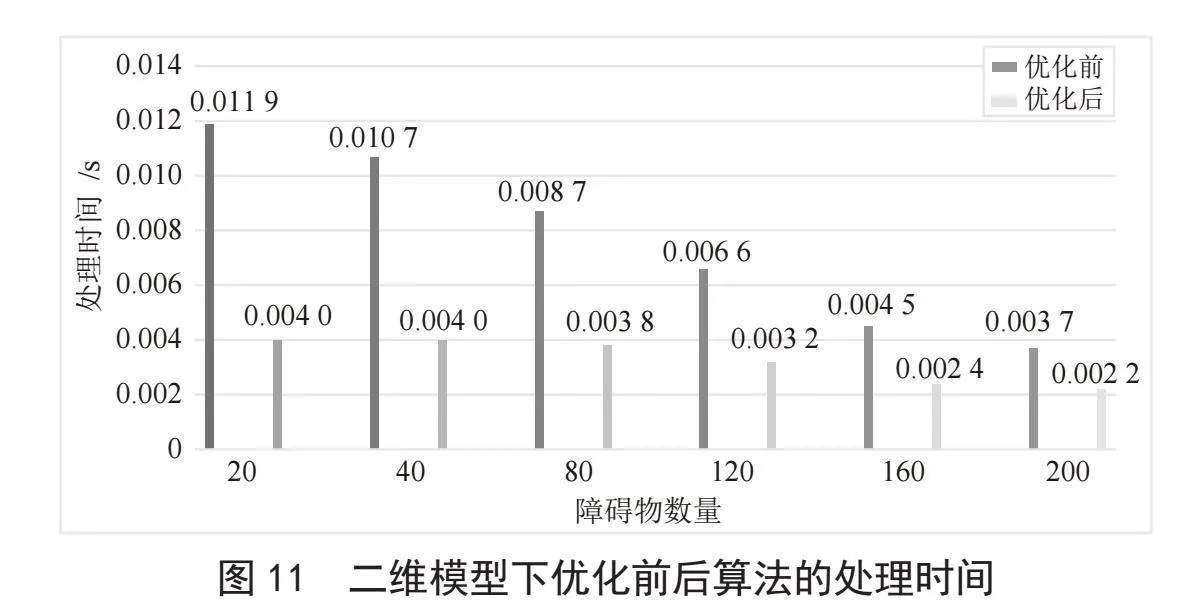
建立一个20×20的二维栅格地图，起点S（0，0）终点G（19，19），将障碍物的数量设置为自变量，随机放置在地图中并每个数量进行2 000次实验记录下处理的时间，并且进行死路处理，得到如图11所示的结果。

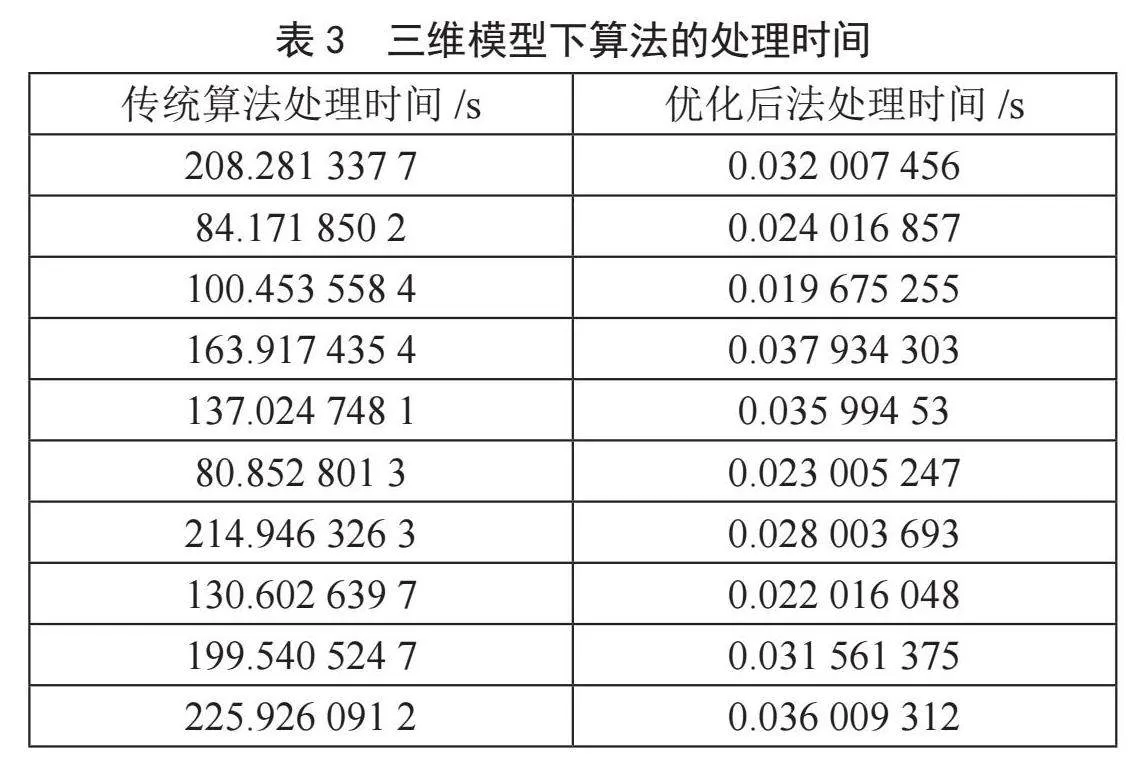
其次，5×5×5的三维模型地图，起点为S（0，0，0），终点为G（4，4，4），并在地图中随机放置不同数量的障碍物。进行10次实验并记录，计算出处理时间的平均值。表3展示了实验结果。

通过实验验证，在生成相同路径的基础上，优化后的自定义优先队列的A*算法明显表现出更高的效率和更短的处理时间，甚至在二维模型中平均优化率达到225.98%。这种差距对于实际应用中的实时性和效率至关重要，特别是在需要快速求解的实时路径规划和导航等场景中。因此，在大规模或复杂问题的求解中，选择本文提出的优化方法能够显著提升算法的执行效率和性能。

5" 结" 论

A*算法在寻路过程中存在内存开销大、计算时间长等缺点，不能满足移动机器人在较大场景路径规划中的实时性要求。为了提高路径规划的速度，本文分别从性能和路径优化上进行讨论，性能上通过实时阈值、二叉堆优先级队列和局部A*算法，提高了寻路效率。路径优化上，通过引进惩罚因子减少拐点数量，从而使。通过在不同规格栅格环境下的仿真实验证明改进A*算法是可行的、有效的，特别是在较大二维场景和三维模型下效果更加明显。

参考文献：

[1] 赵晓，王铮，黄程侃，等.基于改进A*算法的移动机器人路径规划 [J].机器人，2018，40（6）：903-910.

[2] 曲道奎，杜振军，徐殿国，等.移动机器人路径规划方法研究 [J].机器人，2008（2）：97-101+106.

[3] 王殿君.基于改进A*算法的室内移动机器人路径规划 [J].清华大学学报：自然科学版，2012，52（8）：1085-1089.

[4] JEDDISARAVI K，ALITAPPEH R J，PIMENTA L C A，et al. Multi-Objective Approach for Robot Motion Planning in Search Tasks [J].Applied Intelligence，2016，45（2）：305-321.

[5] 周伟，潘金宝，王林琳.基于改进鲸鱼算法和A*算法的地面放线机器人路径规划 [J].现代制造工程，2023（12）：68-75+83.

[6] 王洪斌，尹鹏衡，郑维，等.基于改进的A*算法与动态窗口法的移动机器人路径规划 [J].机器人，2020，42（3）：346-353.

[7] 刘建华，杨建国，刘华平，等.基于势场蚁群算法的移动机器人全局路径规划方法 [J].农业机械学报，2015，46（9）：18-27.

[8] 朱大奇，颜明重.移动机器人路径规划技术综述 [J].控制与决策，2010，25（7）：961-967.

[9] 周小镜.基于改进A*算法的游戏地图寻径的研究 [D].重庆：西南大学，2011.

[10] 安彦哲，朱妤晴，王建民.物联网大数据场景下的分布式哈希表适用条件分析 [J].计算机学报，2021，44（8）：1679-1695.

作者简介：蔡梓丰（2001—），男，汉族，广东佛山人，本科在读，研究方向：移动机器人路径规划。