图像处理中应用图像降噪算法的研究综述

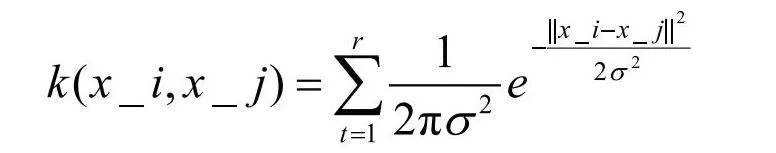
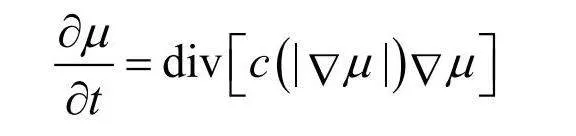
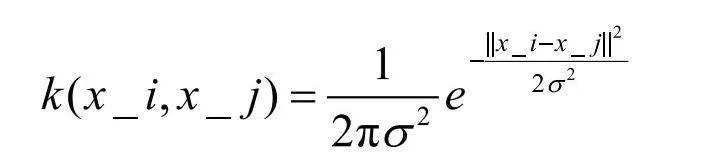
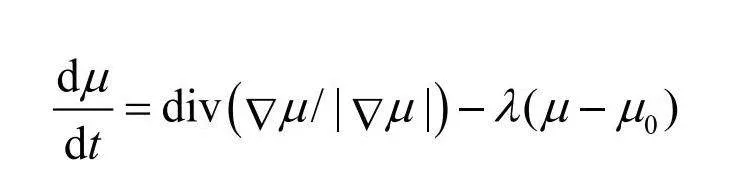
摘" 要：日常生活中，在发送、存储图像和拍照形成图像的过程中往往会因操作不当而导致图像不清晰，无法反映图像本质。为此采用图像降噪算法将图像中的杂质去除，还原出无噪声的图像，同时还可以使大部分的细节因素保留在图片中，让图片更加清晰。在去噪方法的运用上通常是采用无噪图像和含有噪声的先验信息，但弊端是二者并没有进行有效的结合。为了解决这个问题，采用小波、非局部均值等方式进行去噪，并且在非局部均值去噪中从欧氏距离和权重分配方面进行一些优化。

关键词：图像去噪；小波去噪；非局部均值；欧氏距离；权重

中图分类号：TP391" " 文献标识码：A" 文章编号：2096-4706（2024）10-0021-06

Research Review of the Application of Image Denoising Algorithms in Image Processing

BAI Ruxin， LUAN Shangmin

（North China Institute of Science and Technology， Langfang" 065201， China）

Abstract： In the daily life， during the process of sending image， storing image， and taking photos to form images， improper operation often leads to unclear images that cannot reflect the essence of the image. To this end， an image denoising algorithm is used to remove impurities from the image， restoring a noise-free image. At the same time， most of the details can be retained in the image， making it clearer. In the application of denoising methods， noiseless images and prior information containing noise are usually used， but the drawback is that the two have not been effectively combined. To solve this problem， wavelet and non-local mean methods are used for denoising， and some optimizations are made in terms of Euclidean distance and weight allocation in non local mean denoising.

Keywords： image denoising; wavelet denoising; non-local mean; Euclidean distance; weight

0" 引" 言

随着互联网和信息技术的快速发展，人们越来越喜欢用图片和视频来呈现自己的真实写照，例如我们发送的表情包，自拍或者发一段短视频都可以作为信息载体。统计数据表明，近80%的外部信息都是通过眼睛传递的，图像就是主要的来源。

随着生产效率和人们生活水平的不断提高，越来越多的领域开启了图像的使用，例如医疗领域的X光图像、CT图像可用于判断患者骨头及器官的损伤程度，国防科技领域的卫星检测、无人机拍摄等都需要用到图像，在密集人群和公共场所中需要进行图像监控以此确保人身的安全。然而，现实生活中的应用都需要使用高清图像作为支撑，医生需要借助清晰的图像来判断患者的病情，国防上更是不能有半点差错。但是图像在传输和压缩过程中因受各种因素的干扰而产生噪声。噪声的产生会让图片变得不那么清晰，从而影响人们的生活和判断。如何进行高质量降噪以还原出清晰图片是一个非常重要的问题，当下经常采用的方法有高斯噪声、盐和胡椒粉噪音、3D过滤以及非局部均值图像去噪。

1" 图像去噪基础知识

1.1" 噪声分类及去噪算法概述

日常生活中常见的噪声分为两种，一种是高斯噪声又称正态噪声，简单来说就是噪声图是符合正态分布的。高斯噪声对图片的影响是不确定的，常见形式如下：

其中，μ为噪声的数学期望，σ2为图像噪声的方差。当本式的数学期望为0时，图像噪声的方差与它的平均功率相等，概率密度为：

瑞利分布的数字特征为：

另一种是椒盐噪声，也就是常说的脉冲噪声。它是随机出现的黑点或白点，黑点是高灰度噪声，它一般与低灰度噪声同时出现，其概率密度函数表示为：

如果b＞a，那么灰度值b为亮点，a为暗点；如果Pa或Pb为零则变为单极型脉冲噪声。

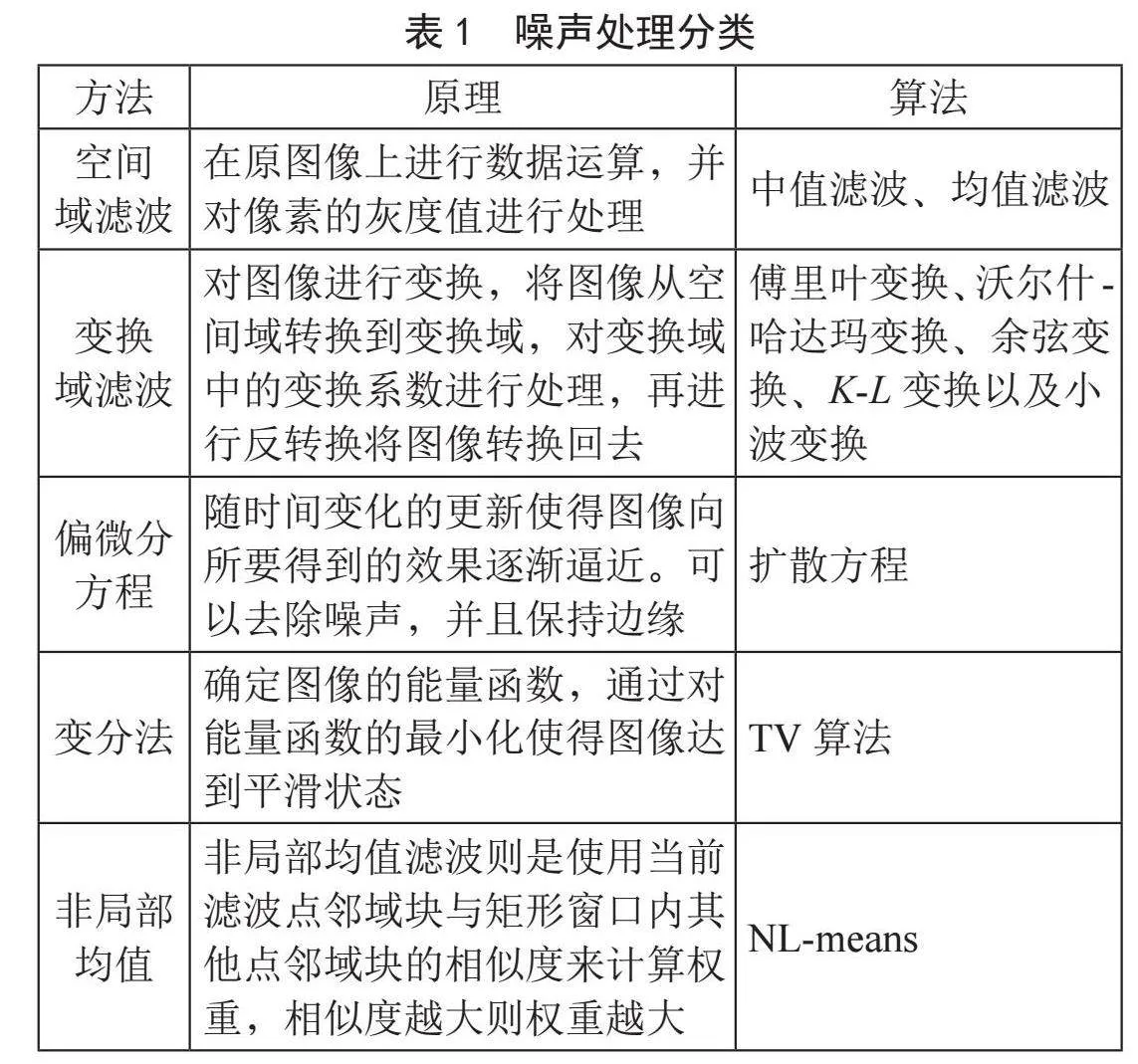
所谓的去噪就是还原出最清晰的图片，同时最大限度保持图片的细节，几种噪声的处理如表1所示。

去噪问题通常被当作逆向的问题来处理，假设一张256×256的噪声图像y，想要通过算法进行去噪，恢复到未被噪声污染的图像把它设为x。那么噪声图像可以表达为：y = x + v，噪声模型如图1所示。

1.2" 国内外研究现状分析

图像去噪在20世纪就是一个人们持续关注的问题，现如今科研人员已经研究出很多种图片去噪方法，并且不断有新的理论在涌现。大致的发展顺序为：Donoho [1]提出一种空间域的算法，率先推出了均值去噪的方法，但是这种滤波无法很好地保护图像的细节，它会破坏图像导致内容的缺失，因为这就是线性方程的弊端，无法在去噪的同时进行图像的边缘检测。为了改变这一现状，Ibrahim [2]提出一种非线性的滤波方式——中值滤波，这种方法对椒盐噪声的去噪效果很好。从此图像去噪就有了另一种思路——频率域去噪，它的主要原理是利用傅里叶变换到频率域进行去噪，高斯滤波就是其中的一种。随着科技的发展，降噪处理的作用越来越明显，小波域滤波[3]在此情景下应运而生。它是一种变换域方法，主要原理就是过滤掉高频信息达到降噪的目的，但是它会将边缘的信息平滑掉。然后就有了偏微分，偏微分具有各向异性，它可以在噪声密度较小时去除噪声并保留图像边缘细节，但随之而来的问题是密度高的时候效果很不理想。2005年，Buades [4]等提出了非局部均值方法，在此基础上又出现了三维块匹配算法，此方法的去噪效果非常理想，成为去噪基准算法。

2" 去除噪声算法概述

2.1" 空间域和频率域去噪

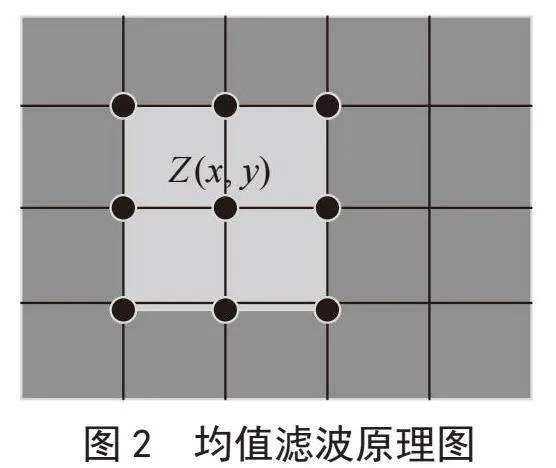
空间域去噪是指通过调整邻域内像素的方式来去除图像噪声，其中均值滤波的原理就是先选择一个中心的像素点，然后取该像素点与其周围像素点的像素平均值，将该像素点滤波后的值替换成平均值，为了方便我们都是采用一个矩形窗口，例如：3×3，5×5，…，（2n + 1）×（2n + 1）。以3×3为例，如图2所示。Z点的滤波值是通过计算周围9个点的平均值而得到的。如果是边缘就扩充边界以此得到平均值。

计算式为：

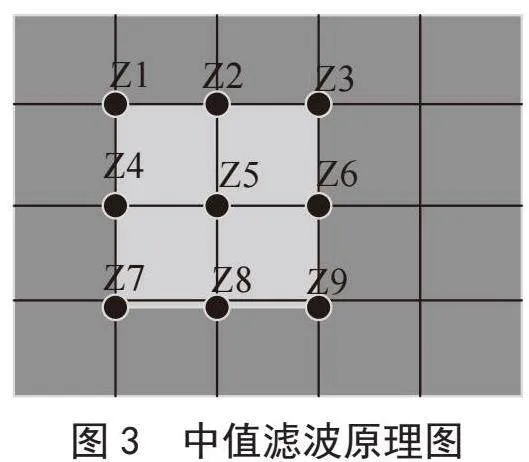
中值滤波就是对邻域像素值进行排序，排序后像素值处于中间的那个就是滤波值。假设对3×3噪声图像的窗口进行中值滤波，如图3所示，我们要寻找一下Z5的滤波值，排序结果为Z1＜Z2＜Z3＜Z5＜Z4＜Z6＜Z7＜Z8＜Z9，那么Z4就是Z5的滤波值。

由此可以看出，找中值的算法是中值滤波的关键。第一种方法是冒泡排序，这种排序方式是最简单也是耗时最长的一种排序，底层逻辑就是反复扫描一个排序序列，通过比较大小来对他们的排序进行调整，直至所有元素都不再发生位置改变，这表明完成了排序。伪代码为：

Bubble_sort（list）： // list 表示待排序序列

for ilt;- 0 to length（list）-1： // 对于元素个数为n的list序列，需遍历n-1次，这里用[0，length（list）-1）表示。

for j lt;- 1 to length（list） - i： // 从第1个元素开始遍历，遍历区间为[1，length（list）-i）。

if list[j] gt; list[j+1]： // 若进行降序排序，则改成小于号＜

swap（list[j] ， list[j+1]） // 交换2个相邻元素的位置

return list

第二种方法就是快速排序，随便选一个“中间值”（一般是一堆数字里面的第一个数字），以这个数字为基准将所有数字分成两堆（一堆是小于等于这个数字的数字，一堆是大于等于这个数字的数字），然后采用递归调用快速排序算法分别对这两堆数字进行排序。伪代码为：

quick_sort（int a[]，int left，int right）{

quick_sort（a，left，m-1）//这两行是递归调用：自己调用自己

quick_sort（a，m+1，right）

}

2.2" 小波滤波

小波最初主要应用于数字和信号处理领域，后来被Mallat [5]引入计算机视觉领域。小波可以被视为一种在传统去噪领域中定位的信号滤波器，并且这种滤波器是在不同尺寸层次上定义的。小波提供一种平滑处理的方式，在不产生块效应的同时把信号分解为频率成分。小波系数处理方式大致可分为：

1）极大值去噪。

2）相邻尺寸小波系数相关性去噪。

3）变换阈值去噪。变换阈值去噪既简单又实用，被大多数人所使用。阈值的选择是非常重要的，阈值过小会导致图像的噪声没法去除干净，阈值太大则会影响图像本身的信息导致图像失真。

阈值的选择大致有两种方法：一种是硬阈值，另一种是软阈值。硬阈值法的计算式为：

其中，α表示选取的阈值（下同），将所选信号的正值与我们预先确定的阈值进行比较，当x的绝对值小于α就为0，x的绝对值大于α则保持不变。软阈值法的计算式为：

将信号的正值与我们预先确定的阈值进行比较，信号的正值小于等于阈值则设为0，绝对值大于阈值，则将其设为信号绝对值与阈值的差。但是阈值选择的缺点也很明显。在这里设计了一个新的阈值函数，其融合了软硬阈值的优点。我们自定义的阈值函数为：

其中，N表示正数，di表示处理前的初始小波系数， 表示处理过的系数函数图像。

2.3" 偏微分方程去噪

利用偏微分方程对图像去噪[6]，基本思想就是将Gaussian核函数与图像相结合做卷积运算。卷积运算的目的是在消除噪音的同时模糊边缘图像。我们将图像看作一块温度不一的导热板，把噪声和边缘的高频信号比作温度高的地方，然后用热传导进行降温，这就是热传导模型的概念。热传导方程的数学表达式为：

其中，Δ表示拉普拉斯算子，μ（0，x，y）表示方程的初始条件为观测到的噪声图像μ0，而μ表示演化的图像。由于拉普拉斯变现的各向同性，图像各个方向的扩散速度和强度一样，因而模糊了边缘。图4（a）为噪声图像，经过30次扩散的图像如图（b）所示，我们可以清晰地看出它已经开始模糊了，经过10 000次扩散的图像如图（c）所示，可以看出整张图的灰度值几乎一致了。

虽然可以缓解噪声，但代价是图像的边缘也被模糊了，可边缘信息又是非常重要的。因此PM模型应运而生，它是从各向同性转为各向异性的扩散方程：

PM模型和热传导的差别就在于多了一个扩散系数c（|∇μ|）。常梯度模大的地方就是边缘，小的地方就是平坦区域，所以PM模型可以进行扩散，还可以进行边缘检测。边缘区域c（|∇μ|）变小，平坦区域c（|∇μ|）变大。然而，图像会产生很多的黑白斑点，因为它会被误判定为边缘的区域，此处的噪声就会留存下来，如图5所示。为了克服PM模型的缺点，TV模型利用全变差范数构造去噪方程，该方程在边界的梯度方向上没有扩散，可以有效地保护图像的边界信息。

2.4" 变分法去噪

在数学领域，变分法[7]是用来研究未知函数影响的，通过对泛函变分得到泛函的极值函数，使用已知的极值函数让泛函取得极大值或极小值。而变分法应用于图像去噪中所用到的主要原理是根据噪声图像的先验知识和数学模型建立一个合适的能量泛函，在求极值的过程中达到降噪的目的。最为经典的就是TV模型，为了克服PM模型的缺点，TV模型利用全变差范数构造去噪方程，这样可以更好地保留边界信息。其数学表达式为：

其中， 为平滑项，表示图像平滑度， 表示保真项，确保去噪时不会偏离原图像。将一维推广到二维，利用变分法的欧拉方程得到：

引入人工时间t，通过有限差分法求解：

随着迭代的进行可得到去噪后的图像，如图6所示。

2.5" 非局部均值算法

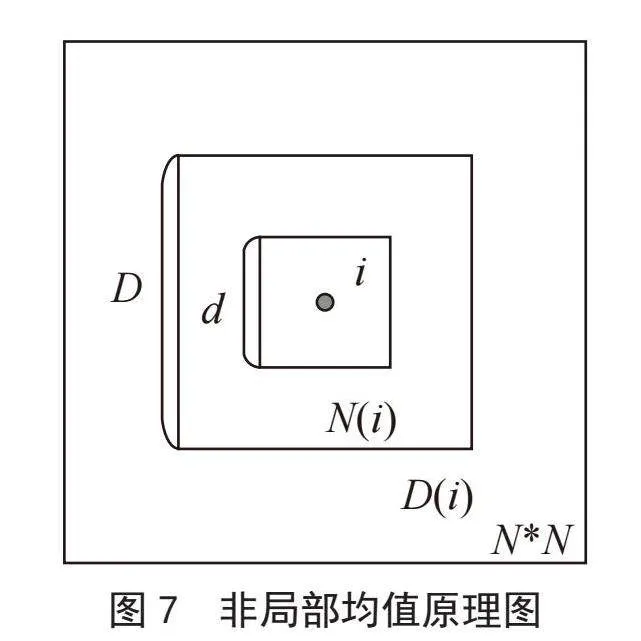
传统非局部均值算法[8]主要是利用图像中的冗余信息，在这个范围内找到一个搜索块，然后进行相似块的匹配，具有很好的降噪效果。传统非局部均值算法的主要步骤如图7所示。

首先在有噪声的图像中创建一个以D为边长的搜索块，再建立一个以d为边长的相似块，并按照如下步骤进行去噪：

1）在搜索块里面找到一个像素点i，以它为中心建立相似块，再找一个像素点建立同样大的相似块，用高斯加权欧式距离计算权重系数：

2）在搜索窗中遍历所有点j。

3）选择权重最大的赋值给i，并将权重归一化，i的像素值为：

4）最后遍历图像所有i点，完成降噪。

图8（a）为原图噪声图像，图8（b）为非局部均值去噪后的图像，可以看出非局部均值算法的降噪效果还是非常不错的。

3" 改进非局部均值算法

如前所述，当下技术最先进、应用最多的就是以非局部均值算法为基础的图像去噪算法[9]，因为这种算法本身存在很多不合理性，有很多专家进行了算法的改进，例如，结合双边滤波和非局部均值算法降低了计算的复杂度，解决了图像边缘失真的问题，提出采用离散余弦变换算法予以改善。虽然这些方法在算法的改进上都取得了一定的成效，但在运行时间、权值分配以及欧式距离计算邻域相似性以突出中心像素方面，仍存在一些问题未能得到很好的解决。我们可以从最基础的非局部均值算法出发，从权值分配和欧式距离计算方式两个方面进行深入探讨，并尝试进行适当的改进，以达到加快算法运行速度的目的。

3.1" 改进欧氏距离计算邻域相似性

传统的非局部均值算法，在计算两个点相似程度时通常使用高斯核函数加权，使用欧氏距离来计算两点的邻域矩阵，高斯核函数计算式为：

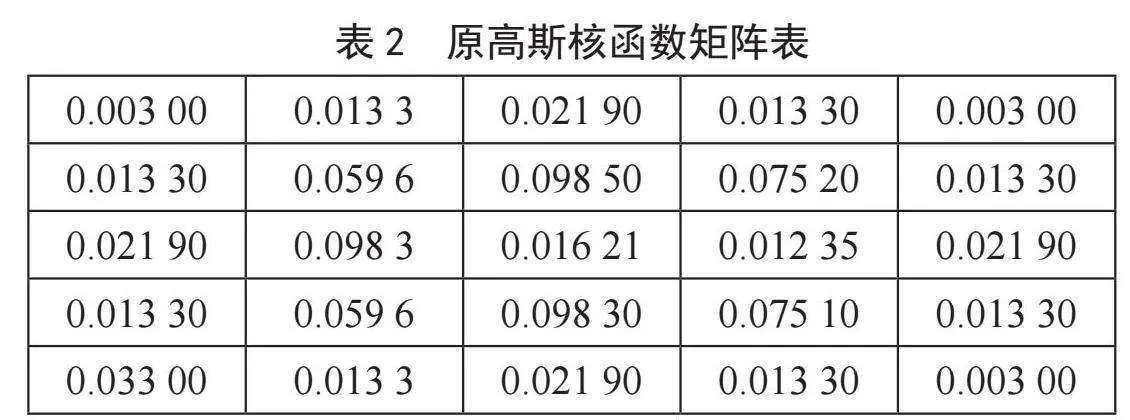
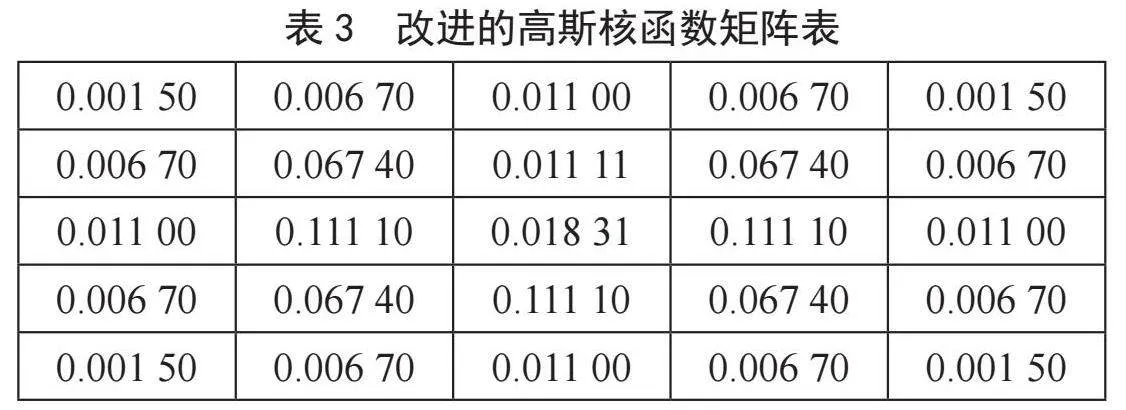
像素点的距离不同对中心点的影响也不同，距离和对中心点的影响成反比，离中心点越近影响越大，但这样也有一个很大的弊端，就是对中心点的重视不足。改进的算法是在高斯核函数的基础上对所有存在的高斯核进行累加操作，从而得到最终的高斯核矩阵结果[10]。计算式为：

从表2和表3中可以看出，传统高斯核矩阵的中心点权重为0.162 1，改进后高斯核矩阵的中心点权重为0.183 1。这完全满足了距离中心点与权重分配的原则，同时当中心像素点作为中心时，其自身的权重值会增大，从而更加凸显中心像素点的地位和作用。

3.2" 改进距离权重函数

传统非局部均值去噪算法一般使用指数型核函数，计算式为：

为有效解决传统非局部均值中对细节模糊程度非常大的问题，将其融入图像领域间的相关系数来评价图像的指标，寻找矩阵之间的相似性，其计算式为：

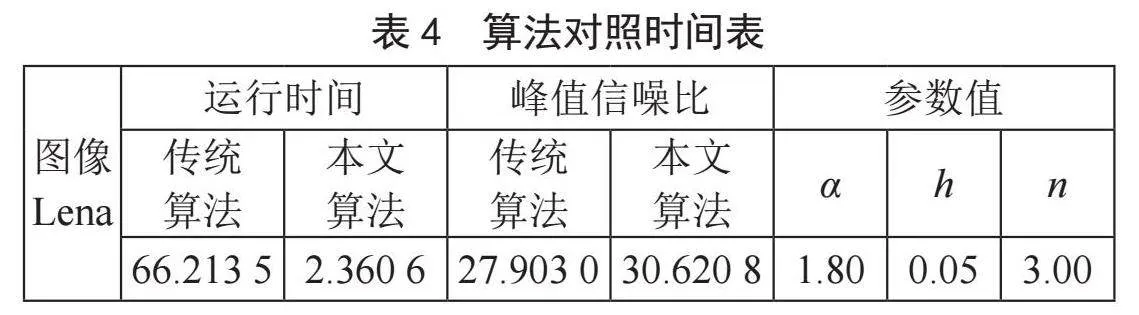
其中， 中的b表示灰度矩阵Na的灰度均值，b1表示灰度矩阵Nb的灰度均值，图像去噪结果如图9所示。可以看到图9（d）图中的帽子细节更加明显，并且从表4中可以看出运行时间的明显减少大大提高了运行效率，同时信噪比也比传统方法的好一些。

4" 结" 论

随着图像降噪领域的快速发展，诸多研究者将非局部均值的方法与其他算法相融合，使降噪技术更加成熟与强大。但图像去噪速度一直是研究人员关注的重要问题，计算相似块的时间复杂度过高，而如今都是采用非常便捷的拍照，这要求我们不光要提高质量更要提高速度。

参考文献：

[1] DONOHO D L，Johnstone L M. Ideal Spatial Adaptation by Wavelet Shrinkage [J].Biometrika，1994，81（3）：425–455.

[2] IBRAHIM H，KONG N S P，NG T F. Simple Adaptive Median Filter for the Removal of Impulse Noise from Highly Corrupted Images [J].IEEE Transactions on Consumer Electronics，2008，54（4）：1920-1927.

[3] CHOI H，BARANIUK R. Multiscale Image Segmentation Using Wavelet-Domain Hidden Markov Models [J].IEEE Transactions on Image Processing： a Publication of the IEEE Signal Processing Society，2001，10（9）：1309-1321.

[4] BUADES A，COLL B，MOREL J M. A Non-Local Algorithm for Image Denoising [C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition （CVPR'05）.San Diego：IEEE，2005：60-65.

[5] MALLAT S，HWANG W L. Singularity Detection and Processing with Wavelets [J].IEEE Transactions on Information Theory，1992，38（2）：617-643.

[6] 张劲松，陈明举，熊兴中，等.一种去除椒盐噪声的自适应非局部均值滤波 [J].四川轻化工大学学报：自然科学版，2022，35（3）：59-65.

[7] 许连杰.基于非局部自相似性的图像去噪算法研究 [D].长春：长春工业大学，2022.

[8] 徐明辉.基于非局部自相似性的像素自适应图像超分辨率 [D].哈尔滨：哈尔滨工业大学，2022.

[9] 郭昕刚，许连杰，霍金花，等.基于非局部自相似性的图像去噪算法研究 [J].计算机仿真，2022，39（9）：364-369+475.

[10] 白列，蔡芸，蒋林.基于区域划分的非局部均值图像去噪算法的改进 [J].软件工程，2023，26（5）：1-5.

作者简介：白茹鑫（1999—），男，汉族，内蒙古人，硕士研究生在读，研究方向：应急信息化；栾尚敏（1968—），男，汉族，山东济南人，教授，博士，研究方向：人工智能及其应用。