一定一动——动点轨迹为线段的最值问题

最值问题是近几年中考的热点与难点之一，其中备受命题人青睐的线段最值问题是一定一动类型. 它有以下特点：线段的一个端点为定点，另一个端点为动点. 解此类型题的关键是构建动点的轨迹（直线型、曲线型）. 下面分三种情况举例说明.

一、定线定距离

例1 如图1，矩形ABCD中，AB = 4，AD = 2，E为AB的中点，F为EC上一动点，P为DF的中点，连接PB，则PB的最小值是（ ）.

A. 2 B. 4 C. [2] D. [22]

解析：如图2，过点P作PQ ⊥ CE于点Q，可证△PQF [∽] △DEF，于是 PQ = [12]DE = [2]. 可知点P到CE的距离始终是[2]，即点P在平行于CE且到CE距离为[2]的直线l上运动，故线段 PB的最小值转化为点B到直线l的垂线段BM的长（如图3），易得BM = 2[2]. 故选D.

小结：若动点P到定直线l的距离为定值，则动点P的轨迹是平行于l的直线.

[A][B][D][C][E][F][P] [A][B][D][C][E][Q][F][P] [A][B][D][C][E][M] [l]

图1 图2 图3

二、定线夹定角

例2 如图4，在矩形ABCD中，AB = 3，∠DCA = 30°，点F是对角线AC上的一个动点，连接DF，以DF为斜边作∠DFE = 30°的直角三角形DEF，使点E和点A位于DF两侧，点F从点A到点C的运动过程中，求CE的最小值.

解析：如图5，以AD为斜边作∠DAG = 30°的Rt△ADG，连接EG，易得[DEDF=DGAD] = [12]，∠EDG = ∠FDA，所以△EDG ∽ △FDA，故∠DGE = ∠DAF = 60°，可知动点E在与DG成60°夹角的射线GE上运动，则CE的最小值转化为点C到该射线的垂线段CH的长（如图6），易得AD = [3]，所以DG = [32]，所以DH = [34]，CH = [94]. 故CE的最小值为[94].

小结：若动点P与定线段AB形成的∠PAB为定值，则动点P的轨迹是一条射线.

[D][C][A][B][E][F] [D][C][A][B][E][F][G] [D][C][A][B][H][G]

图4 图5 图6

类型三：定点等距离

例3 如图7，在平面直角坐标系中，已知A（2，4），P（1，0），B为y轴上的动点，以AB为边构造△ABC，使点C在x轴上，∠BAC = 90°，M为BC的中点，求PM的最小值.

解析：如图8，连接AM，OM，在Rt△OBC中，∠BOC = 90°，M是BC的中点，则OM = [12]BC，同理AM = [12]BC，所以OM = AM，可知动点M的运动轨迹是线段AO的垂直平分线l. 故PM的最小值是点P到l的垂线段PN的长，如图9. 易知D[0，52]，E（5，0），DE = [525]. 连接DP，在△DEP中，由面积法可得PN = [455]. 故PM的最小值为[455].

[A][C][P][O][B][M][x][y] [b78150639ff0b09843f96f2069f6c7d85e361ff3e156d747ef01e1ef5ca62c4cA][C][P][O][B][M][x][y] [A][E][P][O][D][N][x][y][l]

图7 图8 图9

小结：若动点P到两定点A，B的距离相等，则动点P的轨迹是线段AB的垂直平分线.

在一定一动——动点轨迹为线段的问题中，一个动点A运动，往往另一动点B也随点A的运动而运动，同时随点A的确定而确定，即点A与点B之间存在着必然的因果关系，建立起A，B之间的因果关系是解决与动点B相关问题的关键.

拓展训练

1. 如图10，在正方形ABCD中，已知边AB = 5，点E是BC边上一动点（点E不与B，C重合），连接AE，作点B关于直线AE的对称点F，则线段CF的最小值为（ ）.

A. 5 B. [52-5]

C. [522] D. [52]

2. 如图11，在△ABC中，AB = AC = 10，BC = 6，延长AB至D，使得BD = [12]AB，点P为动点，且PB = PC，连接PD，则PD的最小值为（ ）.

A. [92] B. 5 C. [32] D. 9

[B][A][C][D][F][E] [A][B][D][P][C]

图10 图11

3. 如图12，在菱形ABCD中，∠ABC = 120°，E是AB边的中点，P是AC边上一动点，PB + PE的最小值是[3]，则PE的最小值为（ ）.

A. 2 B. [3]

C. 1 D. [33]

4. 如图13，在正方形ABCD中，AB = 4，G是BC的中点，点E是正方形内一动点，且EG = 2，连接DE，将线段DE绕点D逆时针旋转90°得到线段DF，连接CF，则线段CF长的最小值是（ ）.

A. [25] - 2 B. 2 C. 3 D. [5]

[D][C][B][E][A][P] [C][B][G][E][A][D][F]

图12 图13

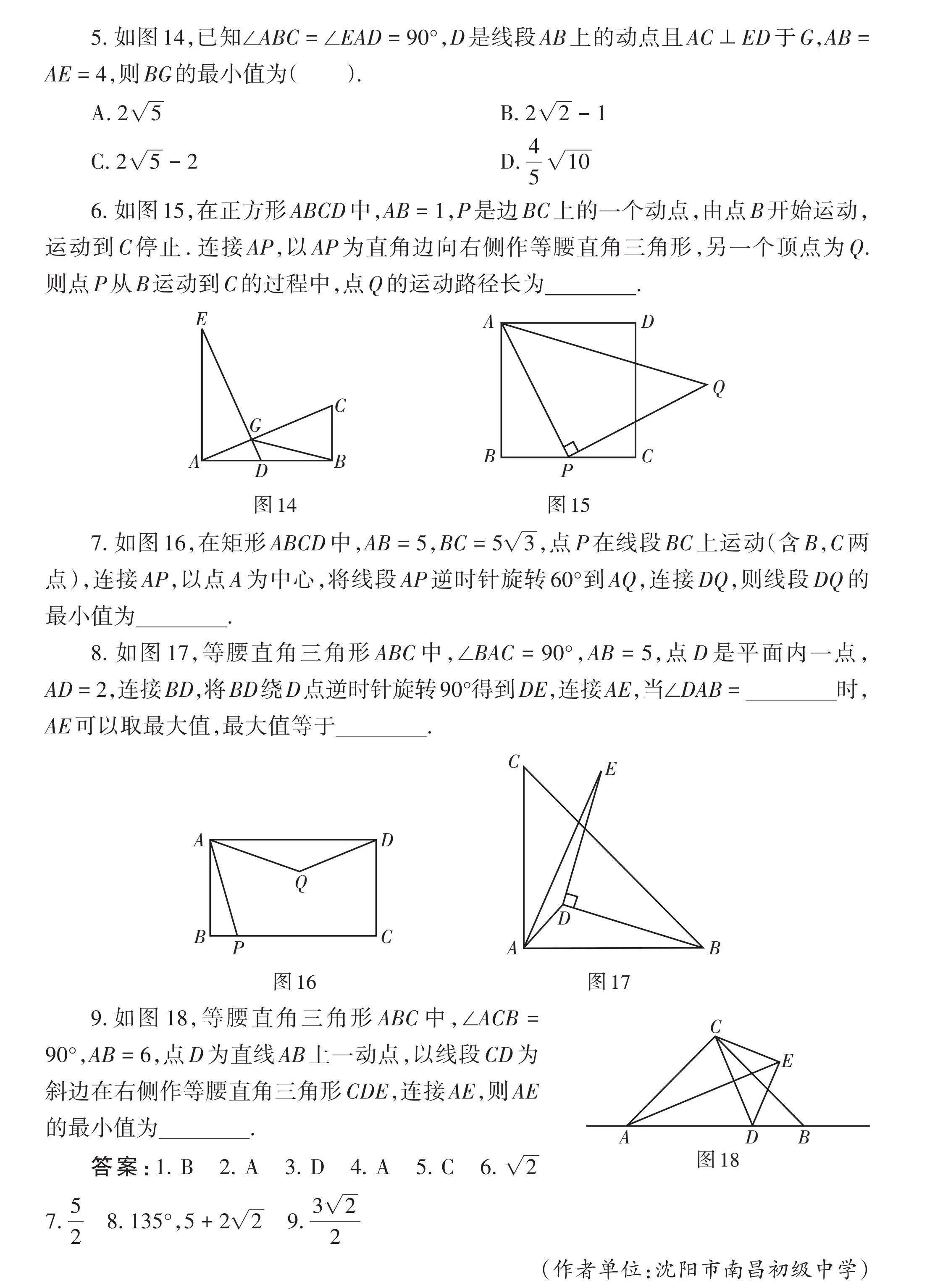
5. 如图14，已知∠ABC = ∠EAD = 90°，D是线段AB上的动点且AC ⊥ ED于G，AB = AE = 4，则BG的最小值为（ ）.

A. [25] B. [22] - 1

C. [25] - 2 D. [4510]

6. 如图15，在正方形ABCD中，AB = 1，P是边BC上的一个动点，由点B开始运动，运动到C停止. 连接AP，以AP为直角边向右侧作等腰直角三角形，另一个顶点为Q. 则点P从B运动到C的过程中，点Q的运动路径长为 .

[A][D][B][C][G][E] [A][D][B][C][P][Q]

图14 图15

7. 如图16，在矩形ABCD中，AB = 5，BC = 5[3]，点P在线段BC上运动（含B，C两点），连接AP，以点A为中心，将线段AP逆时针旋转60°到AQ，连接DQ，则线段DQ的最小值为 .

8. 如图17，等腰直角三角形ABC中，∠BAC = 90°，AB = 5，点D是平面内一点，AD = 2，连接BD，将BD绕D点逆时针旋转90°得到DE，连接AE，当∠DAB = 时，AE可以取最大值，最大值等于 .

[B][P][A][C][D][Q] [A][B][E][C][D]

图16 图17

9.如图18，等腰直角三角形ABC中，∠ACB = 90°，AB = 6，点D为直线AB上一动点，以线段CD为斜边在右侧作等腰直角三角形CDE，连接AE，则AE的最小值为 .

答案：1. B 2. A 3. D 4. A 5. C 6. [2] 7. [52] 8. 135°，5 + 2[2] 9. [322]

（作者单位：沈阳市南昌初级中学）