对三个典型位置物体重力的辨析

摘 要：用非惯性参考系、惯性力等概念去理解重力有其优越性，但这些知识并不适合高中教学的实际情况。针对用万有引力定律理解重力的困惑，以重力是万有引力的一个分力为基础，辨析了地球上空、地球表面和地球内部三个位置物体所受的重力。

关键词：重力；万有引力；自转；分力

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2024）12-0063-3

人教版高中物理必修一中对重力的定义是：由于地球的吸引而使物体受到的力叫做重力［１］，这个定义仅指出了物体重力产生的原因。人教版必修二中提出“若不考虑地球自转的影响，地面上质量为ｍ的物体所受的重力ｍｇ等于地球对物体的引力”［２］，这个定义虽明确指出了物体重力与万有引力的关系，却是有条件的。那么，在地球自转时物体的重力等于多少？在空中和地面以下的重力又如何？如果利用非惯性参考系和惯性力作出解释，显然不适合中学课堂，因此教师需要结合教学实际，厘清物体重力与万有引力的关系。

１ 地球表面物体的重力

１．１ 不考虑地球自转

若不考虑地球自转的影响，地球表面质量为ｍ的物体所受的重力等于地球对物体的万有引力，即

mg=（1）

如果没有区分赤道和两极的重力加速度，或直接交代地表的重力加速度为ｇ，这就表明重力与万有引力相等。将（1）式ｍ消去得到，GM=R2g，这就是俗称的“黄金代换式”［３］，它不仅对其他天体适用，而且涉及到具体计算时误差较小，所以也叫“万能代换式”。

１．２ 考虑地球自转

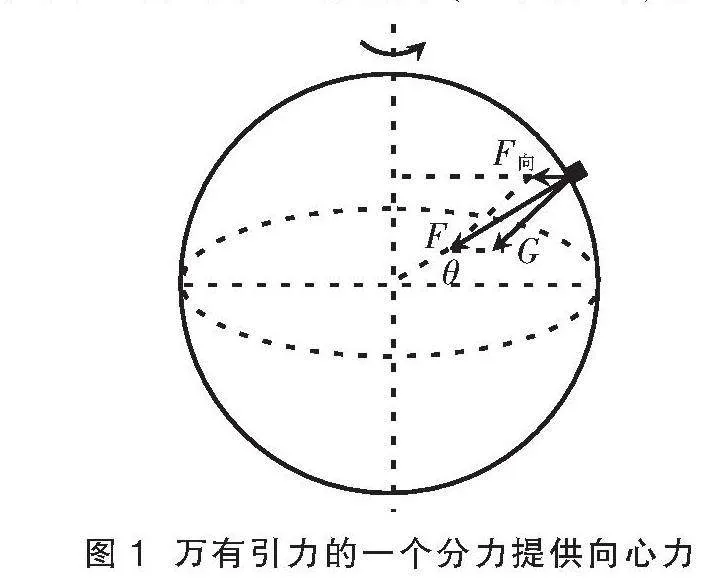
若考虑地球的自转，并将地球视为惯性系，物体随地球一起做圆周运动，除两极外，万有引力的一个分力需要提供垂直指向地轴的向心力，另一个分力就是物体的重力［４］，如图１所示。这时，重力不再等于万有引力（两极除外）。

图１ 万有引力的一个分力提供向心力

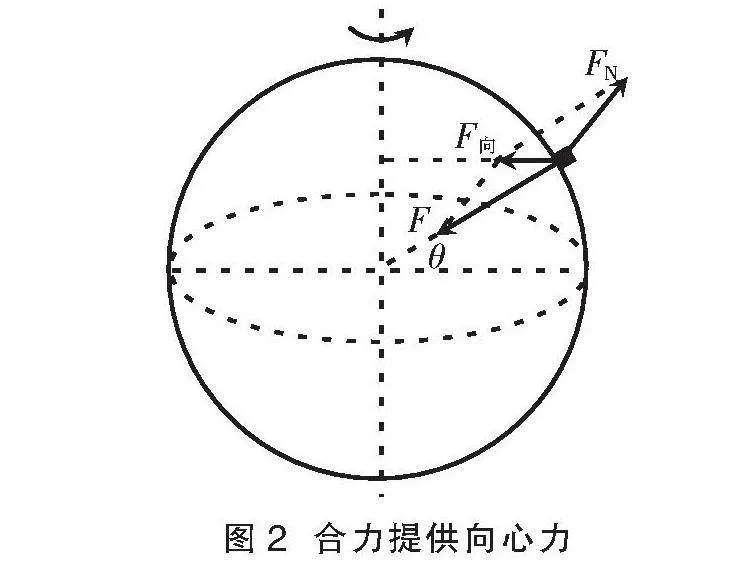
也可以这样理解，物体在地球表面受到两个力，万有引力和支持力，如图２所示，物体的万有引力Ｆ与支持力ＦＮ的合力提供圆周运动的向心力F向，轨道半径ｒ＝Ｒｃｏｓθ。重力等于支持力，它们是一对平衡力。由于物体随地球做圆周运动，所以重力不指向地心（赤道和两极除外）。如图３所示，将mg和Ｆ沿着Ｆ方向分解，满足关系

图２ 合力提供向心力

图3 三力近似关系

mgcosσ=F-Fcosθ=-mRω2cos2θ（2）

因为σ很小，故ｃｏｓσ≈１，将（2）式变形得

mg=-mRω2cos2θ（3）

（3）式表明，θ越大，即物体的纬度越高，那么物体所受的重力就越大。讨论特殊情况：

当θ＝０时，物体处在赤道，mg1=-mRω2；

当θ＝９０°时，物体处在两极，mg2=。

在这里学生会质疑：支持力方向是球体切线的垂线方向，重力的方向就应该指向地心才对，但图１中重力却不是指向地心，这是为何？其实，地球并不是严格的球体，地球表面主要由海水组成，赤道附近的海水比重小，地球自转使得两极距地心近、赤道距地心远形成椭球体，形似“哈密瓜”。如图４所示，支持力垂直于海平面，万有引力指向椭圆中心，万有引力Ｆ与支持力ＦＮ的合力提供物体圆周运动的向心力F。

图４ 哈密瓜形

以上是在惯性系下解释了物体所受重力与万有引力的差异，特别是用椭球体解释重力的方向，学生容易理解，如果不纠结重力方向的问题，完全可以将地球简化为球体。不过，高中阶段主要考查赤道和两极处物体的重力，这两处重力的方向与万有引力的方向相同。

２ 地球上空物体的重力

２０２２年１１月３０日，神舟十五号成功将三位航天员费俊龙、邓清明、张陆送入中国空间站，与神舟十四号航天员乘组首次实现“太空会师”，他们将在轨生活半年，完成２０２２年的第六次飞行任务。航天员们在空间站里面处于完全失重状态，按照失重的概念，当物体对悬挂物的拉力或对支持物的压力等于零时，物体处于完全失重状态，所以完全失重只能说明航天员的视重为０，并不代表航天员就没有重力。那么，在地球上空，物体所受的重力等于什么？

假设ｈ高处有一颗卫星绕地球做匀速圆周运动，万有引力提供卫星做圆周运动的向心力，有=F向。此时卫星已脱离地球，重力不再受自转的影响，（3）式中的ω＝０，但（3）式还是可以用来计算重力，即mg=，所以

mg==F向（4）

（4）式表明，当物体绕地球做匀速圆周运动时，重力等于万有引力，重力就是万有引力的一个代名词而已，此时也可以说重力提供了卫星圆周运动的向心力。（4）式还表明，物体所受重力随高度ｈ的增加而减小，对于卫星而言，高度ｈ少则也有几十千米。如果只是几层楼的高度，那就只能当作地面上的物体来处理，参考系也会随之改变，因为当ｈ远小于地球半径Ｒ时，完全没有必要考虑海拔高度对重力的影响，即使是在最高峰珠穆朗玛峰的顶端，重力加速度也仅比海平面的小不到３‰［５］。

以上分析了在高空不受地球自转影响时物体的重力，下面再来分析一下在高空且受地球自转影响时物体的重力。假想从赤道铺设一条竖直的电梯至同步卫星，设地球自转角速度为ω，当物体上升至某一高度ｈ（ｈ≤ｈ０）时，物体受到万有引力和电梯的支持力，支持力等于重力，有

mg'=-m（R+h）ω2（5）

当物体上升至同步卫星的高度ｈ０时，满足等式

=m（R+h0）ω2（6）

联立（5）（6）式，解得

mg'==

（7）

由（7）式得，当ｈ＜ｈ０时，物体的重力随高度的增加而减小；当ｈ＝ｈ０时，物体的重力等于０。这说明空中物体的重力还与地球自转的角速度有关。

３ 地球内部物体的重力

如果物体到了地表以下，那重力又如何呢？教学中，我们会碰到结论“质量分布均匀的球壳在其内部产生的引力场场强处处为零”。这个结论可以用微元法证明（证明略），也可以采用类比法理解，因为点电荷间的静电力公式与物体间的万有引力公式形式相同，电场强度与引力场场强的表达形式也相同，既然均匀带电的球壳内部电场强度处处为零，那么“质量均匀的球壳在内部产生的引力场场强处处为零”也成立。

受上面结论的启发，如图５所示，可以将地球分为厚度ｈ的球壳与半径（Ｒ－ｈ）的球体两个部分，认为地球是质量分布均匀的球体，那么物体在ｈ处的重力就等于半径为（Ｒ－ｈ）的球体对它的万有引力，有

mg1=

M=ρ·πR3

M1=ρ·π（R-h）3

得到mg1=，当ｈ增大（深度变大）时，重力减小。令R-h=x，得到

mg1=∝x（8）

图５ 地球分为两部分

由（8）式可知，距离地心ｘ处的物体重力与ｘ成正比，当ｘ＝０，即ｈ＝Ｒ时，得到地心处的重力为０。

如果以地球某一直径挖出一条贯穿地球的隧道，并规定正方向，容易证明

F=-πGρmx=-kx∝x（9）

（9）式可以说明物体在这个隧道里面做以地心为平衡位置的简谐运动。

４ 启 示

综上所述，高中阶段只要不考虑地球的自转或区分赤道与两极的重力，那么重力与万有引力就是相等的，但是不能等同［６］；如果考虑地球的自转，限于高中不讲非惯性系与离心惯性力的概念，所以只能认为重力是万有引力的一个分力，尽管这一观点与“重力是万有引力与惯性离心力的合力”存在一定的分歧［７］。总之，任何知识的学习都不是一蹴而就的，随着学习的不断深入，我们对知识的认识会更全面、更深刻。

参考文献：

［１］人民教育出版社，课程教材研究所，物理课程教材研究开发中心．普通高中教科书物理必修第一册［Ｍ］．北京：人民教育出版社，２０１９：５５．

［２］人民教育出版社，课程教材研究所，物理课程教材研究开发中心．普通高中教科书物理必修第二册［Ｍ］．北京：人民教育出版社，２０１９：５１．

［３］段石峰．高中阶段如何理解重力和地球引力的关系［Ｊ］．湖南中学物理，２０２２（９）：７８－８０．

［４］金清镇．重力与万有引力谁是“合力”［Ｊ］．物理教师，２０１５，３６（３）：５９．

［５］人民教育出版社，课程教材研究所，物理课程教材研究开发中心．普通高中教科书物理必修第二册教师用书［Ｍ］．北京：人民教育出版社，２０１９：５１．

［６］王太军，唐忠敏．关于重力定义的再探讨——重力与万有引力应该“分家”［Ｊ］．物理教师，２０１０，３１（１０）：３６－３８．

［７］马亚鹏．重力与万有引力的关系及其对中学物理教学的启示［Ｊ］．中学物理教学参考，２０１３，４２（６）：５０－５２．

（栏目编辑 蒋小平）

收稿日期：2024-05-17

作者简介：张育森（1981-），男，中学一级教师，主要从事高中物理教学工作。