对２０２４年高考物理湖南卷第１５题的分析与拓展

摘 要：对２０２４年高考物理湖南卷第１５题进行分析，重点讨论此题的第（２）问，并将此问拓展为“若小球Ａ与Ｂ之间为弹性碰撞，且所有的碰撞位置刚好位于正多边形的各个顶点，求小球Ａ、Ｂ的质量比”。证明了只要小球Ａ、Ｂ在某正多边形顶点发生弹性碰撞，以后各碰撞位置必然在该正多边形的某顶点。并利用数学归纳法，得到拓展问题的一般结论。

关键词：碰撞；动量守恒；能量守恒；质量比

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2024）12-0044-4

《普通高中物理课程标准（２０１７年版２０２０年修订）》中指出，学业质量水平４是高等院校招生录取的学业水平等级考试的命题依据。在学业质量水平４中，学生需要“能理解所学的物理概念和规律及其相互作用……能将实际问题中的对象和过程转换为所学的物理模型；能对综合性物理问题进行分析和推理，获得结论并作出解释……能分析相关事实和结论，提出并准确表示可探究的物理问题……”［１］。２０２４年高考物理湖南卷第１５题便能充分考查学生是否达到了学业质量水平４。该题是两球发生多次正碰的压轴大题，考查运动、相互作用、能量以及动量相关知识。由于碰撞的种类和两球质量关系不明确，需要考生根据题意对碰撞的三种情形（弹性碰撞、完全非弹性碰撞和非完全弹性碰撞）进行分情况分析、讨论和推理，从而得出结果，能全面考查学生的核心素养。现对此题进行分析并拓展。

１ 原题呈现

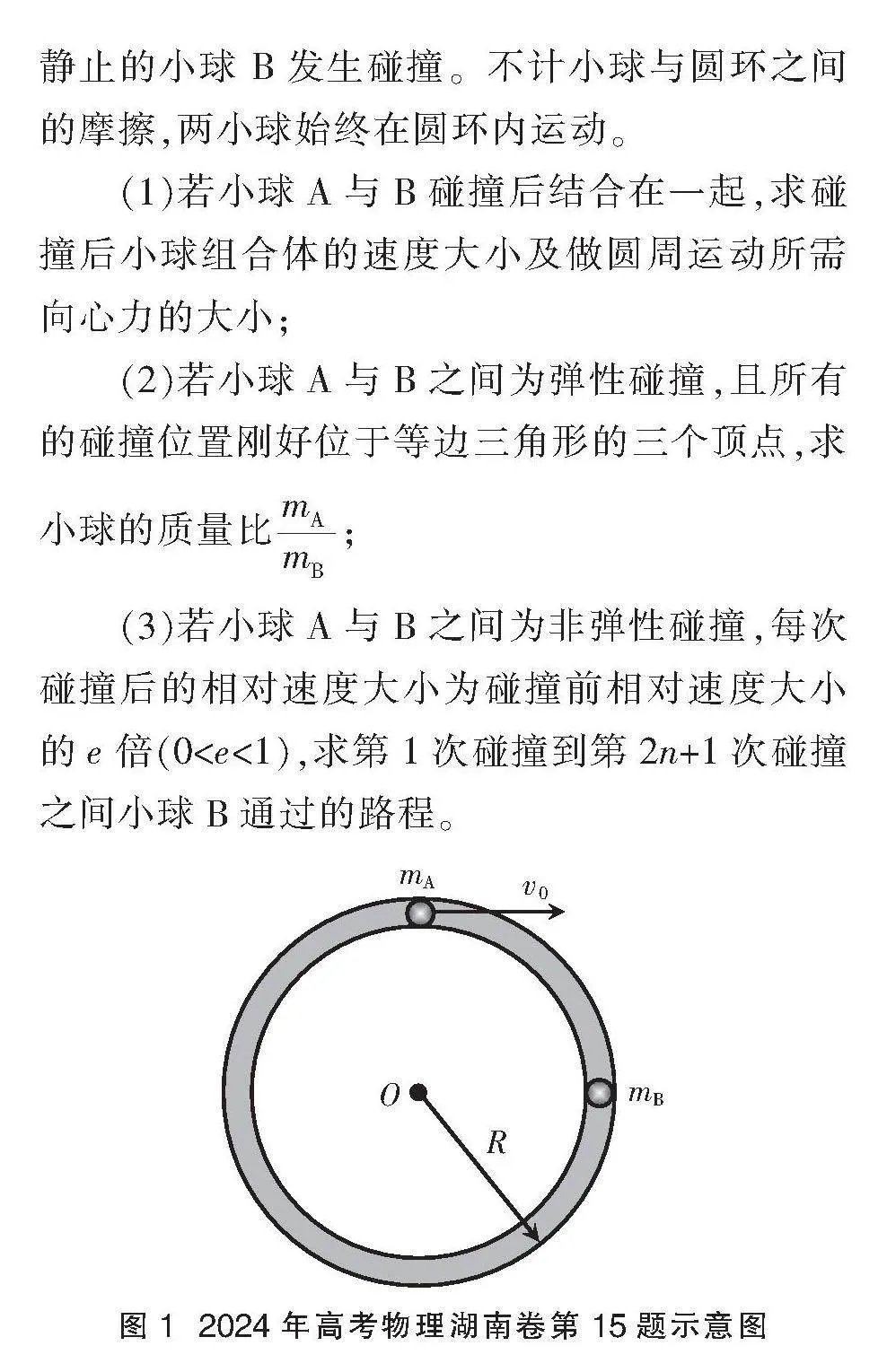
（２０２４年高考物理湖南卷第１５题） 如图１所示，半径为Ｒ的圆环水平放置并固定，圆环内有质量为ｍＡ和ｍＢ的小球Ａ和Ｂ（ｍＡ>ｍＢ）。初始时小球Ａ以初速度ｖ０沿圆环切线方向运动，与静止的小球 Ｂ发生碰撞。不计小球与圆环之间的摩擦，两小球始终在圆环内运动。

（１）若小球Ａ与Ｂ碰撞后结合在一起，求碰撞后小球组合体的速度大小及做圆周运动所需向心力的大小；

（２）若小球Ａ与Ｂ之间为弹性碰撞，且所有的碰撞位置刚好位于等边三角形的三个顶点，求小球的质量比；

（３）若小球Ａ与Ｂ之间为非弹性碰撞，每次碰撞后的相对速度大小为碰撞前相对速度大小的ｅ倍（０＜ｅ＜１），求第１次碰撞到第２ｎ＋１次碰撞之间小球Ｂ通过的路程。

图１ ２０２４年高考物理湖南卷第１５题示意图

２ 试题简评

本题是２０２４年高考物理湖南卷第１５题，作为压轴大题考查碰撞问题。在《普通高中物理课程标准（２０１７年版２０２０年修订）》［１］中对碰撞的内容要求为：通过实验，了解弹性碰撞和非弹性碰撞的特点。定量分析一维碰撞问题，并能解释生产生活中的弹性碰撞和非弹性碰撞现象。从题目设置而言，本题所考查的内容完全符合课程标准的要求。

本题涉及牛顿第二定律、能量守恒定律以及动量守恒定律，旨在考查学生对物体运动、物体之间相互作用规律以及能量的理解与应用。本题第（１）问相对容易，学生利用完全非弹性碰撞特点，结合牛顿第二定律与动量守恒便可顺利解决。学生要完全解决此问题的第（２）与第（３）问，需要对碰撞有更深的理解，仅仅停留在表面是不行的。本题第（２）问需要学生利用弹性碰撞的特点，根据动量守恒与能量守恒，计算得到小球Ａ和Ｂ第一次碰后的速度vA、vB。此后，需根据题目中已知条件“所有的碰撞位置刚好位于等边三角形的三个顶点”，分析得到从第一次碰撞到第二次碰撞之间Ａ、Ｂ通过的路程之比，进而利用二者的速度之比推导得到二者的质量之比。值得注意的是，此小题还需分情况讨论，即第二次碰撞的位置有两处。本小题容易忽略的是，学生通过上述分析得到小球Ａ、Ｂ的质量比之后没有对以后的碰撞是否均发生在等边三角形的三个顶点进行证明，这于此小题而言是必不可少的。本题第（３）问，学生需要灵活应用题目中的已知条件“小球Ａ与Ｂ之间为非弹性碰撞，每次碰撞后的相对速度大小为碰撞前的相对速度大小的ｅ倍（０＜ｅ＜１）”。深刻理解相对运动，利用非弹性碰撞的特点，根据动量守恒定律进行分析以解决问题。另外，此小题还需学生具有数学归纳能力，能通过计算，找到每次碰撞后到下次碰撞前小球Ｂ所经过路程的规律，此题便可迎刃而解。因此，本题需要学生有较强的模型建构能力、分析与逻辑推理能力，是对学生核心素养的综合考查。

本文重点对第（２）问进行分析并进行拓展，得到“若小球Ａ与Ｂ之间为弹性碰撞，所有的碰撞位置刚好位于正多边形的各个顶点时，小球Ａ、Ｂ的质量比”的一般结论。

３ 试题解析

若两球发生弹性碰撞，设碰后速度分别为ｖＡ、ｖＢ，则碰后动量和能量守恒，有

mAv0=mAvA+mBvB

mAv=mAv+mBv

联立解得v=v，v=

所有的碰撞位置刚好位于等边三角形的三个顶点，如图２所示。

图２ 碰撞位置刚好位于等边三角形的三个顶点示意图

情况１：若第二次碰撞发生在图２中的ｂ点，则从第一次碰撞到第二次碰撞之间，Ａ、Ｂ通过的路程之比为（其中，k1=0，1，2，3…），因此有

==（k1=0，1，2，3…）

联立解得=，由于两质量均为正数，故ｋ１＝０，即=2。

证明：第二次碰撞，设Ａ和Ｂ碰撞后的速度大小分别为v'A、v'B，则同样有

mAvA+mBvB=mAv'A+mBv'B

mAv+mBv=mAv+mBv

联立解得v'A=v0，v'B=0，故第三次碰撞发生在ｂ点，第四次碰撞发生在ｃ点，以此类推，满足题意。

情况２：若第二次碰撞发生在图２中的ｃ点，则从第一次碰撞到第二次碰撞之间，Ａ、Ｂ通过的路程之比为（其中，k2=0，1，2，3…）。所以

==

联立可得=，因为两质量均为正数，故ｋ２＝０，即=5。

证明：根据情况１的分析亦可证v'A=v0，v'B=0，满足题意。

综上可知，=2或=5。

４ 试题拓展

将此题进行拓展：若小球Ａ与Ｂ之间为弹性碰撞，且所有的碰撞位置刚好位于正多边形的各个顶点，求小球的质量比。该拓展便将此题从一个特殊的问题延伸至一个一般的问题，现对此问题进行讨论。

４．１ 证明：各碰撞位置一定为某正多边形的各顶点

如图３（ａ）所示，小球Ａ以速度v0与小球Ｂ在ａ位置发生第一次碰撞，碰后速度分别为vA和vB。第二次碰撞位置假设在图３（ａ）中的ｂ位置，小球Ｂ以速度vB与小球Ａ发生第二次碰撞，第二次碰撞后小球Ａ、Ｂ的速度分别为v'A与v'B，考虑弹性碰撞，可得出v'A与v'B的一般解

v'A=

v'B=

代入试题解析中所得的vA与vB，可得v'A=v0，v'B=0，即小球Ａ与小球Ｂ发生第二次碰撞后，小球Ａ的速度又为初速度v0，小球Ｂ的速度变为零，这种情况与碰撞的位置无关。那么，如图３（ｂ）所示，第三次碰撞依旧发生在位置ｂ处，且第三次碰撞情况同第一次在ａ位置的碰撞情况相同。假设第四次碰撞在ｃ位置处，不难得知，这与第二次碰撞情况相同，且必有弧ａｂ等于弧ｂｃ。以此类推，则可证明小球Ａ、Ｂ若在某正多边形顶点发生弹性碰撞，以后各碰撞位置可能在该正多边形的某顶点。

（a） （b）

图３ 小球Ａ、Ｂ碰撞情况示意图

４．２ 对正多边形进行分情况讨论

４．２．１ 所有的碰撞位置刚好位于正四边形的各个顶点

如图４所示，若第二次碰撞发生在ｂ点，与试题解析中的解析类似，则有==（k3=0，1，2，3…），可得=（k3=0，1，2，3…），k3取0，得=。若第二次碰撞发生在ｃ点，则有==（k4=0，1，2，3…），即=（k4=0，1，2，3…），解得=3。若第二次碰撞发生在ｄ点，则有==（k5=0，1，2，3…），即=（k5=0，1，2，3…），解得=7。

图４ 碰撞位置刚好位于正四边形的四个顶点示意图

４．２．２ 所有的碰撞位置刚好位于正五边形的各个顶点

如图５所示，若第二次碰撞发生在ｂ点，同理有==（k6=0，1，2，3…），即=（k6=0，1，2，3…），解得=。若第二次碰撞发生在ｃ点，则有==（k7=0，1，2，3…），即=（k7=0，1，2，3…），解得=。若第二次碰撞发生在ｄ点，则有==（k8=0，1，2，3…），即=（k8=0，1，2，3…），解得=4。若第二次碰撞发生在ｅ点，则有==（k9=0，1，2，3…），即=（k9=0，1，2，3…），解得=9。

图５ 碰撞位置刚好位于正五边形的五个顶点示意图

４．２．３ 数学归纳与分析

至此，利用数学归纳法，可得到若小球Ａ与Ｂ之间为弹性碰撞，所有的碰撞位置刚好位于正多边形的各个顶点，则小球的质量比的通项公式

=（0<m<n，k=0，1，2，3…）

其中，ｎ为正多边形的边数，ｍ、ｋ均为正整数。由于质量比为正数，故而可将上述通项公式改写为

=（0<m<n）

将该式进一步改写为

===1+（0<m<n）

可知，若ｎ与ｍ相差１，便对应着最大的质量比（）max=2n-1；若m=1，则对应着最小的质量比（）max=，该质量比始终大于１，与题意ｍＡ＞ｍＢ相符。故而，还可以将此题进行拓展，若ｍＡ<ｍＢ，小球Ａ、Ｂ的质量比也可类似上述分析进行求解，此处不再赘述。

５ 小 结

通过对２０２４年高考物理湖南卷第１５题进行分析可知，此题作为压轴大题，考查学生的核心素养，要求学生能利用所学知识，建构物理模型，并在此基础上，通过分析、推理以及归纳和概括得到正确结论，能较好地实现对人才的选拔。本文在原题基础上，对第（２）问进行拓展，拓展的目的并非要让问题变得复杂，而是通过分析发现可以得到更一般、简洁的结论。教师在教学中应注意对教学问题的拓展与延伸，通过拓展，可帮助学生避免进入机械刷题的误区，引导学生在新的较为复杂的情境中对综合性物理问题进行分析和推理，发展科学思维，从而培养学科核心素养。

参考文献：

［１］中华人民共和国教育部．普通高中物理课程标准（2017年版2020年修订）［S］．北京：人民教育出版社，２０20．

（栏目编辑 陈 洁）

收稿日期：2024-07-01

基金项目：成都市教育局立项成都市教育科学规划课题“‘三新’背景下提升学生物理核心素养的多学科融合教学研究”（ＣＹ２０２３Ｙ０８８）；四川省教育学会２０２３年度教育科研立项课题“中学全学科多样态阅读教学实践研究”（ＹＢ２０２３１６８）。

作者简介：罗恒（１９９６－），男，中小学二级教师，主要从事高中物理课堂教学工作。