STEM理念下初中数学项目式学习活动设计

在现代教育中，综合与实践领域的学习越来越受到重视。《义务教育数学课程标准（2022年版）》明确指出，初中阶段应主要采用项目式学习的方式，以问题解决为导向，让学生在真实、多样且具有挑战性的情境中，综合应用多学科知识，解决实际问题。然而，当前一些学校在实施STEM教育的过程中，对数学、物理、化学等领域的融合还不够深入。在此背景下，费马点问题作为一个经典的平面几何优化问题，是一个理想的教学主题。它不仅在数学领域具有重要地位，也与日常生活中的选址问题紧密相关。教师以STEM理念采用项目式学习的模式教学，可以融合物理、数学等知识，引导学生探索解决集散点位置规划的实际方法。学生将经历完整的5E学习环教学过程，即认识问题、设计实验并动手操作、原理解释、模型精致和评价反思，能够深入研究费马点问题，构建起完整的知识体系。

学生参与这种跨学科的学习，不仅能够提升数学素养，还能激发对科学和技术的兴趣。下面，将结合案例阐述如何将这一理念应用于教学中。

一、5E学习环教学模式

5E学习环是美国生物学课程研究会（BSCS）开发的一种建构主义教学模式，包括5个教学环节，即参与、探究、解释、精致和评价。表1对这5个教学环节进行了说明，并阐述了每个环节教师和学生的主要任务[1]。

5E学习环是一种有效的具有实践性、思维性、探究性的科学教育方法，其应用有助于增进学生对知识的理解。这一特征与STEM理念相契合。基于5E学习环设计STEM项目式学习，可以有效帮助学生构建概念，培养探究能力。

二、“规划集散点位置”项目式学习活动的设计

费马点问题是数学领域中平面几何优化的经典议题。它与我们经常遇到的选择最佳位置的优化问题息息相关。华罗庚先生曾将这一问题形象地比喻为“集散点问题”，其中所求的最优点即被称为费马点。在生活中，我们将集散点问题转化为数学中的非线性规划问题，采用微积分中求偏导数的方法，可以发现这一问题与力学中的力平衡有着紧密的联系[2]。

教学对象为九年级学生。他们已经在八年级掌握了二力平衡的基本概念，且能够寻找数学中基础的最短路径。此外，他们还学习了旋转的相关知识，学有余力者可以在“将军饮马”问题的基础上研究三条线段和最小的问题，增加学习的趣味性和挑战性。为此，笔者设计一系列探究实验，让学生通过物理实验和数学论证的双重途径，自行探索并找到最优点，从而更深刻地理解费马点问题。如此实验不仅能够加深学生对费马点的理解，还能激发他们对数学和物理的兴趣，培养他们的实践能力和创新思维。

（一）设计思路

笔者根据5E学习环的各环节内涵，基于“规划集散点位置”项目式学习活动设计了“五环节九步骤”教学流程（如图1）。

在参与环节，笔者设计了与学生日常生活密切相关的问题，引导他们将这些问题与物理力学中的力平衡概念相联系，从而在学生已有的二力平衡知识基础上搭建桥梁。同时，利用微课帮助学生掌握力的合成法则，为后续实验探究明确目标。在探究环节，学生设计并操作实验，观察实验现象，记录关键数据。在解释环节，笔者让学生运用物理和数学知识解释实验结果，尝试构建费马点问题的初步模型。进入精致环节，笔者设计一系列变式实验，以帮助学生深化对费马点问题的理解，完善他们对模型的认识，并应用新知识解决新问题。在评价环节，学生需要对自己的实验操作和知识掌握情况进行自评和互评。同时，笔者对整个学习过程中表现出色的小组或学生给予积极评价，并针对存在的问题提出改进建议。

（二）设计环节

1.参与环节

【创设情境】如图2所示，李阿姨经营便利店，为了提升营业额，推出了“送货上门”服务。经过观察，她发现客源集中在A、B、C三个小区，且业务量大致相等。李阿姨计划效仿物流公司的运营模式，设立一个“外送业务”的集散点，先将部分货物存放于此，再分发到A、B、C三个小区。为降低运输成本，她希望找到一个点，使得从该点到这三个小区的总距离最短。然而，如何找到这个集散点的最佳位置让李阿姨感到困惑，于是她向正在大学攻读物理专业的儿子求助。

李阿姨的儿子指出，这个问题实际上涉及物理中的三力平衡原理。那么，为什么这个问题会与三力平衡有关呢？这是因为在物理学中，寻找一个点使得它到三个固定点的距离之和最小，类似于在力学中寻找三个力的平衡点，使得合力为0。应用这一原理可以帮助李阿姨有效地解决集散点选址的问题。

【预备知识】关于力的平衡学生应该不陌生，他们已经学习过二力平衡，知晓作用在同一物体上的两个力，如果大小相等、方向相反，并且在同一条直线上，这两个力就彼此平衡。学生学习微课并思考：如果两个力不在同一条直线上，那么对于物体的作用效果是怎样的呢？如何理解上述问题中的“三力平衡”呢？为什么要寻找到三个小区的距离之和最短的集散点位置，这与物理学中力的平衡的知识有什么关系吗？

原理解读：根据物理弹性力学中的平衡态公理（又称最小势能原理）可知，当一个质点受到几个始终分别指向某个定点的力时，若物体处于稳定平衡状态，即质点所受合力为0，则该体系处于势能最小状态。进一步可以推出这样的结论 ：质点处于稳定平衡状态时，该质点到几个定点的单程距离或多程距离之和最小[3]。

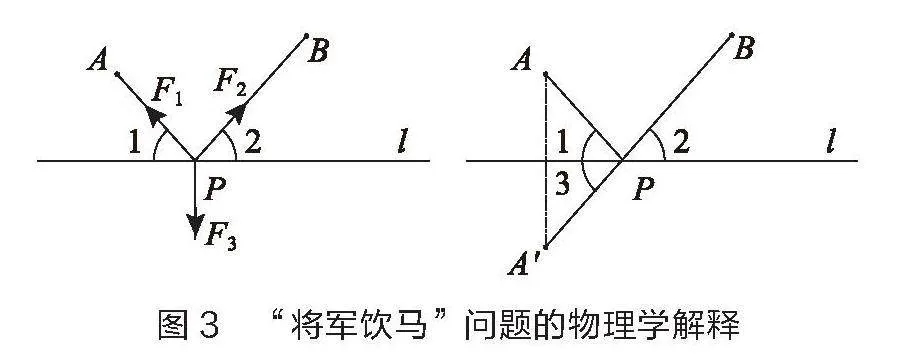
原理应用：大家熟悉的最短路径问题“将军饮马”就可以用物理学的知识来解释。如图3所示，A、B为直线l同侧的两个定点，点P为直线l上的一个动点，当AP+BP最小时点P的位置在哪？此时，将动点P视为一个质点，它分别受到指向A、B的两个力F1和F2。由原理可知，当点P处于稳定平衡状态，即点P所受三个力的合力为0时，AP+BP的值最小。此时，F1和F2在直线l方向的分力相等，因此当AP、BP与直线l所成的夹角相等，即∠1=∠2时， AP+BP最小。这与我们解决“将军饮马”问题的几何解法是一致的，作点A关于直线l的对称点A'，连接A'B，与直线l的交点P即为所求。易知∠1=∠3，∠2 =∠3，即∠1=∠2。

设计意图：借助微课清晰讲解力的合成遵循的“平行四边形法则”和三力平衡相关知识。基于二力平衡的物理实验，探索“将军饮马”问题中的动点位置，以此作为预备知识传授给学生。这样不仅能够培养学生提取和应用信息的能力，还能为后续的实验设计和操作打下坚实的基础。

【明确目标】关键任务是从微课中获取灵感，设计实验，帮李阿姨找到集散点的位置，即满足这个位置到三个小区的总距离最短这一条件。

2.探究环节

有了参与环节的铺垫，学生已经明确了探究问题，掌握了基础知识。此时笔者以问题驱动的方式引导学生设计实验。

预设问题：三个小区的相对位置对集散点的选取是否有影响？如何体现三个小区的位置？如何体现“A、B、C三个小区业务量大致相等”？

学生首先思考问题，分组合作，讨论设计物理实验的操作步骤，然后阐述小组选择的实验方式及理由，预测实验结果等，最后在全班范围内讨论，选择一个最优化的实验步骤。

实验器材：木板、手动打孔器、小圆环、细线、50 g砝码（三个）、量角器等。

实验分五步进行。第一步：将地图中的问题抽象出一个△ABC，从地图中测量出AB、AC、BC的长度及内角的角度，根据三条线段长度比例关系，确定三个小区的相对位置。第二步：选择一块木板，将△ABC画在木板上，在三个顶点处钻孔并打磨光滑。第三步：选择长度适中的三根细绳，将一端穿过小洞，另一端系在木板上方的一个小圆环上。第四步：将三个质量相等的砝码分别挂在三根细绳上，先使细绳保持不受力状态，再将三个砝码同时松手，小圆环静止时就是三力平衡的状态。第五步：在三力平衡的情况下，采用测量线段长度、角的度数等方式观察小圆环的位置有什么特点。

3.解释环节

学生完成操作后发现，小圆环停在△ABC内部，如将小圆环抽象成点P，会发现∠APB、∠APC和∠BPC的大小均约等于120°（如图4）。笔者引导学生分组交流，思考为什么在三力平衡状态下，这三个角都近似为120°，进而思考这个点P是否能满足PA+PB+PC最小这一条件。

本环节笔者给学生充足的思考时间，适时予以点拨，帮助学生运用物理和数学知识，从角度和长度等视角分析点P。

从物理的角度看（如图5），F1=F2，根据力的合成法则（平行四边形法则），可知合力F方向必与菱形对角线重合。处于平衡状态时，第三个力F3与合力F等值、反向。根据菱形的性质，易证这三个力间形成的张角都是120°。

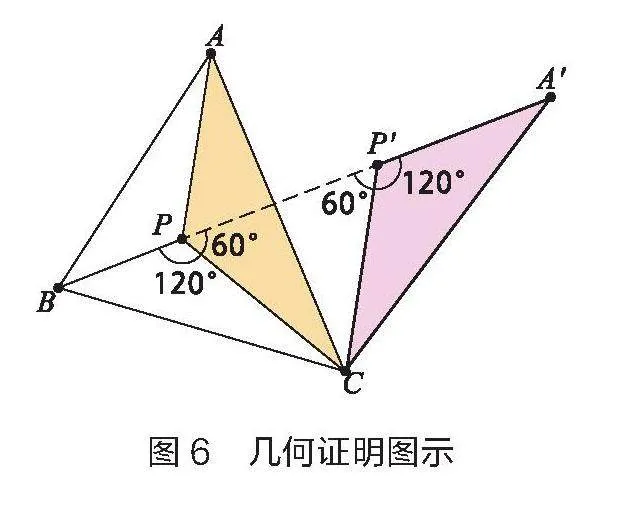
从数学的角度看，学生已经掌握验证距离之和最短的基本方法，就是经过一系列的图形变化将几条线段转化到同一条直线上。此时恰好是线段和最短的时候。如图6所示，将△APC绕点C顺时针旋转60°，△PCP'为等边三角形，可知∠PP'C=∠P'PC=60°，根据前面实验得到∠BPC=120°，易证BP、PP'、A'P'共线。根据旋转的性质可知，PA+PB+PC=A'P'+P'P+PB=A'B。为更加形象地说明共线时是线段之和最小的时候，笔者再任选一点P，根据两点之间线段最短的原理加以说明。

学生从不同视角审视分析后对集散点的位置有了清晰的认识，有助于确定点P的位置。此时，学生很容易想到数学中的“定位神器”——点的坐标。学生通过分组讨论，班内分享，明确了确定点的位置的基本方案，即借助两次旋转变换后形成的直线求出交点坐标。

此时，笔者借助数学软件GeoGebra快速求解，确定点P的位置，并引导学生利用方位角的知识准确表达集散点位置。将实际问题中三个小区的相对位置按 1∶20000缩小后，以点B为原点建立坐标系，构建△ABC，利用软件计算可得到点P的坐标，也可以采用方位角进行表述：李阿姨大约应在B小区北偏东69°，距离B小区0.76 km的位置设置集散点。

4.精致环节

通过前面几个环节的探究与解释，学生基本掌握寻找集散点的方法和原理。笔者提出一个新问题，让学生思考。

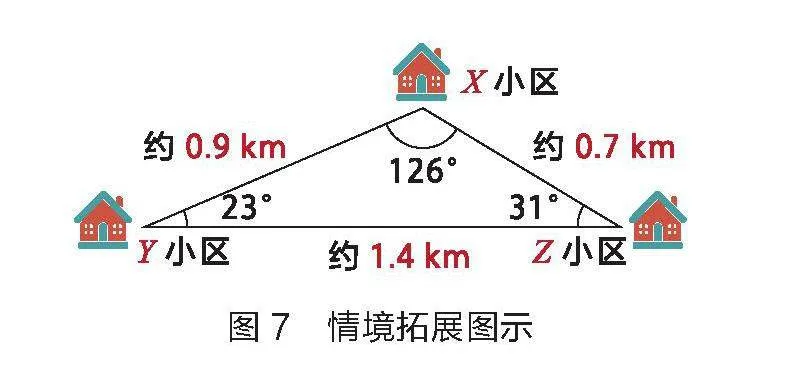
情境拓展：李阿姨根据大家设计的解决方案设立了集散点P，取得了很好的销售业绩，准备进一步拓展业务。如图7所示，李阿姨这次打算针对X、Y、Z三个小区也开设一个集散点。能否按照前面的实验操作帮助李阿姨解决问题？

设计意图：在前面几个环节中，师生共同探究出了三个内角均小于120°的费马点的情况。精致环节中，主要是让学生对于费马点问题进一步加深认识。为节省时间，笔者演示物理实验。此时，小圆环停止在X小区的位置，与前面的探究结果产生矛盾。以此引导学生关注这一问题中出现的大于120°的内角，让学生尝试从物理学和数学视角解释问题。

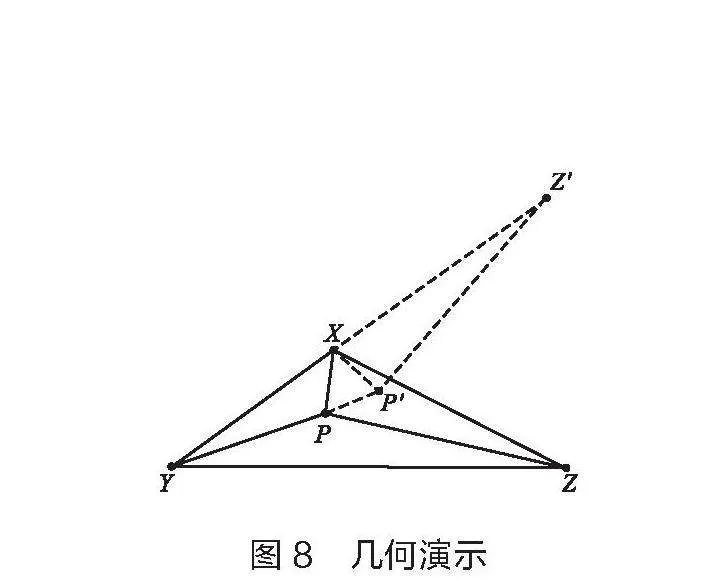
解决问题：与前面的实验一样，由于F1= F2，且力的合成遵循平行四边形法则，故合力F必然在菱形的对角线方向上。但由于两个力的张角大于120°，可知合力F要小于第三个力F3。因此，小圆环会落在X小区的位置。从数学角度也可证明。如图8所示，将△XPZ绕点X逆时针旋转，使得XZ'与XY共线，由于∠YXZ＞120°，可知∠ZXZ' ＜60°，即旋转角小于60 °，所以∠PXP' ＜60°，所以PX＞PP'，PX +PY+PZ＞PP'+PY+P'Z'＞YZ'= XY+XZ'，也就是说当点P和点X重合时，距离之和最小。

此时学生发现，将集散点设置在X小区内，距离之和最短。在师生共同解决这一问题后，笔者给出费马点的定义：费马点是指位于三角形内且到三角形三个顶点距离之和最短的点。学生回顾整个实验操作过程总结得出结论：若三角形三个内角均小于120°，那么费马点在三角形内部 ；若三角形有一个内角大于等于120°，则费马点在钝角顶点处。此时，学生对于三角形中的费马点问题的认知结构得到进一步完善。

5.评价环节

笔者引导学生回忆实验操作过程，以及原理解释过程，总结收获，反思不足。引导学生从学习解决问题的思想方法的角度进行总结。例如：在三力平衡的学习上是类比迁移了二力平衡的知识；探寻费马点的数学原理解释的过程应用到了数学抽象，运用旋转变换转化线段；模型精致阶段大于120°问题的提出，体现了分类讨论的思想等。更重要的是培养了学生的综合能力，即学会分析情境中的各种信息，并用科学合理的方式加以抽象，从而更好地解决问题。

三、教学实施建议

（一）整合信息技术，提高课堂教学效率

STEM课程以其跨学科的特性，强调学生、学科以及社会之间的紧密联系。在现实生活中，许多实际问题并非理想化，若仅依靠人工处理，不仅耗时，还可能掩盖问题研究的本质。根据认知负荷理论，人在学习过程中能够处理的信息量是有限的。因此，教师应利用信息技术直观展示知识，并辅助学生处理复杂的计算问题，可以提高课堂效率。例如，在项目式学习中，将力的合成和三力平衡的概念以微课形式呈现，既通俗易懂又便于学生应用；在解释环节确定点P的位置时，利用GeoGebra软件可以直接获得坐标，有效减轻学生的认知负担，提高效率。

（二）精心设计STEM课程，实现“手脑”协同发展

笔者开展STEM课程教学，将技术、工程学科与科学、数学教育置于同等重要的位置，强调了过程与实践的重要性。在设计STEM课程时，教师应重视学生的动手实践环节，确保活动既具有思考性又具备可操作性，让学生在数学和科学的理论知识指导下，完成实验操作和模型制作等活动。以三力平衡模拟实验为例，教师需引导学生将实际问题抽象成数学模型，并在“实践”与“思考”的互动中，实现“手脑”的协同发展。

（三）促进学科交叉融合，完善学生知识体系

STEM课程的丰富性不仅体现在多学科的交叉融合中，近年来“STEM”还向“STEAM”拓展，引入了人文艺术教育。这表明学科之间并非孤立存在，而是相互联系。数学作为基础学科，虽然具有理论性和抽象性，却是许多学科研究的基础。一种有效的方法是从现有的数学教学资源出发，寻找与其他学科的联系，设计项目式学习活动。教师将数学的理论性与物理的实践性相结合，可以让学生对知识有更深刻的理解，从而完善学生的知识体系，充分发挥STEM教育的价值。

参考文献

[1] 王健，李秀菊.5E教学模式的内涵及其对我国理科教育的启示[J].生物学通报，2012（3）：39-42.

[2] 张莲莲，黄忠裕，俞胜涛.几类特殊的费马点问题及其初等解法[J].中国科教创新导刊，2011（22）：87.

[3] 邓清.基于平衡态公理的一类最短路径问题探究[J].中国数学教育，2022（8）：56-59.

（作者胡玺舜系天津师范大学滨海附属学校教师；佘文娟系天津师范大学滨海附属学校高级教师）

责任编辑：祝元志