基于Beta-SARMA模型的安徽降雨量预测

摘要：本研究旨在通过Beta-SARMA时间序列模型捕捉安徽省降水模式，为农业产出、灌溉需求和农民福祉提供可靠数据支持。该模型在传统SARIMA模型的基础上，结合广义线性回归，并将残差设定为Beta分布。研究发现，皖中和皖南地区的降水数据残差符合高斯分布，而皖北地区则表现出不同的分布模式。Beta-SARMA模型在预测性能上普遍优于传统SARIMA模型，显示出更高的准确性和可靠性。

关键词：降水量预测；广义线性回归；Beta-SARMA模型；R语言

降水预测在全球范围内被视为一个至关重要的研究领域，其对农业、水资源管理以及整个社会经济活动产生着深远的影响。随着气候变化的加剧和极端天气事件的频繁发生，准确的降水预测变得越来越重要，以便各国政府和相关机构能够及时采取适当的应对措施。近年来，科学家们已经采用了多种创新方法来提高降水预测的准确性。例如，王永涛等人开发的中长期降水预测模型就是一次重要尝试。该模型利用小波分解技术结合预测重建过程，有效提取了降水数据中的关键特征，从而改善了预测的准确度[1]。另一方面，郭楠和王兆才采用了结合了麻雀搜索优化算法的BP神经网络和马尔可夫链，这种组合模型能够更好地处理降水的非线性变化[2]。此类发现不仅在理论上有重要意义，也为实际的水资源管理和应急响应提供了实用的指导。

安徽省在地理上属于华东地区，处于暖温带过渡地区，以淮河为分界线，北部属暖温带半湿润季风气候，南部属亚热带湿润季风气候。安徽省南北两部的代表性城市的历年降水量数据对研究安徽省降雨变化特征对农作物产量预报及因地制宜指导农业生产有着重要的意义[3-5]。

1 材料与方法

1.1 数据资料

选用的降雨量数据来源于历年安徽省统计年鉴，收集了2000—2021年共计22年的安徽省16市（巢湖市不做分析）逐月降雨量资料，2000—2020年为训练数据集，2021年为验证集。

1.2 研究方法Beta-SARMA模型

时间序列分析广泛应用在按时间顺序收集的数据上，ARIMA模型是一个著名的时间序列分析模型，在降雨预测中起十分重要的作用[6]，ARIMA模型由自回归（AR）部分、积分（I）部分和移动平均（MA）三部分组成。然而，需要注意的是，ARIMA模型基于对数据的高斯（正态）分布假设。这意味着它们假定数据遵循一个钟形曲线，而这不一定适用于所有类型的数据。特别是对于那些季节性是由随机过程引起的数据集，ARIMA模型可能不太适用。在这种情况下，广义线性回归给出了另一种使用非高斯模型的办法，这种模型可以有效处理数据中的随机机制驱动的季节性，并更好地捕捉数据背后的机制[7]。Beta-SARMA模型[8]是一个动态类的时间序列模型衍生自贝塔回归模型。Beta-SARMA[9]模型集成了随机季节、自回归和移动平均动力学三个组成部分。假设是n个随机变量的向量，对于每一个服从一个β分布，模型的表达式为：

这里的，是模型的自回归和移动平均的系数，而和是季节性自回归和移动平均的系数。P和q分别是模型的自回归部分和移动平均部分的阶数，P和Q分别是描述季节自回归部分和季节移动平均部分的阶数，S表示季节性频率。

1.3 均方根误差（RMSE）

在进行时间序列分析和预测时，评估模型的预测准确性是至关重要的。为此，研究者经常使用各种误差指标来量化模型的预测能力。其中，均方根误差[10]（RMSE）是最常用的评价指标之一，因为它综合考虑了所有预测误差，并提供了一个易于解释的单一值。均方根误差（RMSE）计算公式为：

2 结果与分析

考虑到安徽省的地理和气候特征[11]，本研究将全省的16个城市依据地理位置划分为三个主要区域：淮河以北（包括宿州、淮北、蚌埠、阜阳、亳州五市）、江淮之间（合肥、淮南、安庆、六安、滁州五市）以及长江以南（黄山、芜湖、马鞍山、铜陵、宣城、池州六市）。选择了三个具有代表性的城市—安庆、亳州、黄山进行深入展示与分析。

2.1 模型建立及检验

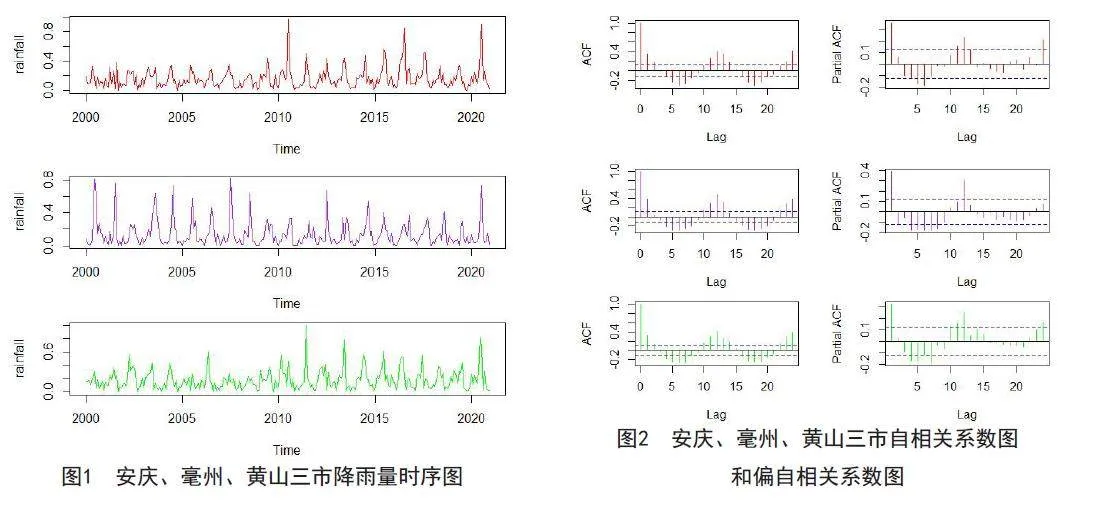
Beta-SARMA模型的构建基于对残差行为采用Beta分布，这要求将原始降雨量数据转换至（0，1）的范围内。图1清晰展示了安庆、亳州和黄山三市在2000—2020年，经过此转换处理的降雨量数据时间序列。在时间序列分析中，若序列的均值与方差随时间保持恒定，则称该序列为平稳的。使用ADF检验来测试三个城市的降雨量数据是否平稳，检验结果为所有城市的P值均低于0.05的临界值，这表明安庆、亳州和黄山的降雨数据满足平稳性需求。

图2展示了安庆、亳州和黄山三市降雨量的自相关系数图（ACF）和偏自相关系数图（PACF）。安庆市的ACF图在初期显示显著的非季节性峰值，而季节性成分在滞后12处表现突出。亳州市的ACF和PACF图则显示明显的季节性和非季节性成分。黄山市的数据呈现初期的非季节性显著峰值及季节性成分的周期性特征，表明三市降雨量时间序列中存在非季节性和季节性波动。

在确定了所有可能的非季节性自回归（p）和移动平均（q）成分，以及季节性自回归（P）和移动平均（Q）成分的组合后，使用R软件并通过AIC准则选择了每个城市的最佳Beta-SARMA模型。表1列出了三市最佳Beta-SARMA模型及其参数估计值。表1中的Ljung-Box[12]检验结果表明，Beta-SARMA模型成功拟合了安庆市和黄山市的降雨量数据，而亳州市的Ljung-Box检验P值显著小于0.05，表明该模型未能有效捕捉亳州市的降雨模式。

2.2 模型预测

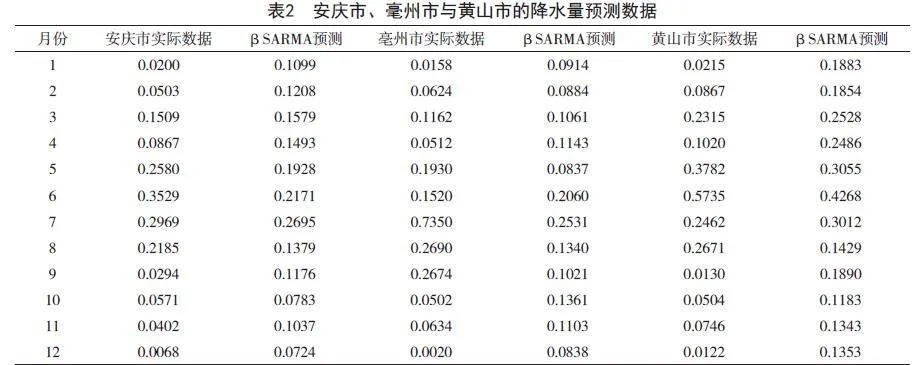
表2详细展示了2021年三个城市的实际降水量与Beta-SARMA模型预测值之间的对比。

从表2可以看出，得出Beta-SARMA模型在这三个城市的均方根误差（RMSE）分别为0.07276、0.14838和0.11514。与之形成对比的是，采用传统SARIMA模型在同一时间段内的预测结果，其均方根误差分别为0.07758、0.12996和0.11514。特别值得注意的是，在安庆市和黄山市，Beta-SARMA模型展现出的预测精度明显优于传统SARIMA模型，这一发现凸显了在特定气候和地理条件下，Beta-SARMA模型的高效性和适应性。

深入分析三市原始降水数据揭示了一些关键的地理和气候特征。亳州市的月均降水量较低，其数据分布频繁出现低于下四分位数的情况。这可能是由于亳州市地处淮河以北的平原区域，该地区降水量普遍偏低，导致数据呈现出显著的偏态分布。此类偏态分布的数据对于线性模型的预测挑战较大，不适合简单的线性拟合。相比之下，安庆市和黄山市月均降水量均超过100 mm，降水量较为丰富。在这两个城市中，Beta-SARMA模型通过将降雨量数据有效地转换至（0，1）[13]区间，显著提高了预测的准确性，从而在预测性能上超越了传统SARIMA模型。

此外，对安徽省其余13个市近20年的月降水量数据进行深入分析，采用R语言挑选出适合各个城市的最佳Beta-SARMA模型，并利用auto.arima函数自动选择最合适的SARIMA模型。这些模型的12期预测结果与实际降水量数据对比后得出的均方根误差（RMSE）如表3所示。结果显示，Beta-SARMA模型在合肥、安庆、六安等11个城市的预测中表现优异，其中10个城市位于皖中和皖南地区。

3 结论

采用Beta-SARMA时间序列模型对安徽省十六个市的降水进行预测，主要发现：通过自相关系数图（ACF）、偏自相关系数图（PACF）和Ljung-Box检验分析Beta-SARMA模型的残差，皖中和皖南地区的降水数据残差似乎符合高斯分布，而皖北地区则不然。这可能与皖北为暖温带半湿润大陆性气候，年降水量较少且集中在夏季有关；而皖南为亚热带湿润气候，年降水量丰富，特别是夏季降水充沛，表明Beta-SARMA模型更适用于降水量较大的区域。与SARIMA模型的RMSE误差估计对比，Beta-SARMA模型在多数情境下显示出明显更高的预测精度，验证了其优越性能。

参考文献

[1] WANG Y，Liu J，LI R，et al.Medium and long-term precipitation prediction using wavelet

decomposition-prediction-reconstruction model[J].

Water Resources Management，2022，36（3）：971-987.

[2] GUON，WANG Z.A combined model based on sparrow

search optimized BP neural network and Markov chain

for precipitation prediction in Zhengzhou City，China[J].

AQUA-Water Infrastructure，Ecosystems and Society，2022，71（6）：782-800.

[3] 朱国良，严韬，秦粮朋等.安徽省旱涝受灾时空特征及与降水关系研究[J].安徽农业大学学报，2020，47（6）：971-978.

[4] 张梦瑶，郑谦.长三角城市群农业信息化发展水平测度[J].安徽科技学院学报，2022，36（3）：97-102.

[5] 魏新彦，刘颖，张俊飚.气候智慧型农业项目能否抑制农业碳排放——来自安徽气候智慧型主要粮食作物生产项目的经验证据[J].浙江农业学报，2023，35（3）：676-687.

[6] 咬登魁，段功豪.基于季节性SARIMA模型的武汉市长序列降雨量趋势分析与预测[J].地下水，2022，44（2）：166-168.

[7] 李莎，林晖.结合MLR和ARIMA模型的时空建模及预测[J].计算机工程与应用，2021，57（13）：276-282.

[8] SHAD M，SHARMA Y D，NARULA P.Forecasting

Southwest Indian Monsoon Rainfall Using the Beta Seasonal

Autoregressive Moving Average（β SARMA）Model[J].Pure and Applied Geophysics，2023，180（1）：405-419.

[9] BAYER FM，CINTRA RJ，CRIBARI-NETOF.Beta

seasonal autoregressive moving average models[J].Journal

of Statistical Computation and Simulation，2018，88（15）：2961-2981.

[10] 吴雪梅，刘志强，张天龙，等.双模型结合进一步降低预测均方根误差和均方根相对误差的方法[J].分析化学，2015，43（5）：754-758.

[11] 郑基超；倪泽强.安徽融入长三角研究——基于生态环境和基础设施建设视角[J].时代金融，2019（23）：45-47.

[12] 聂巧平，孙淇铭.时间序列模型的Ljung-Box检验的发展与应用综述[J].统计与管理，2022，37（4）：101-107.

[13] 张春华；高铁梅；陈飞.经济时间序列频率转换方法的研究与应用[J].统计研究，2017，34（2）：92-100.