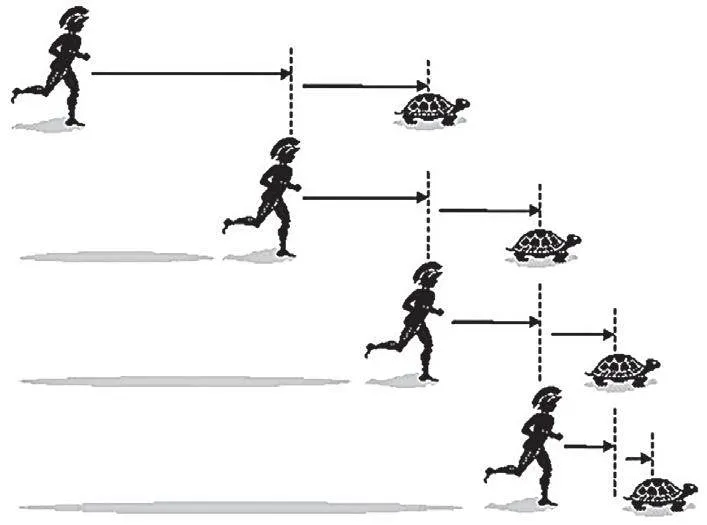
芝诺悖论

当谈到同时存在两种互相排斥的想法这一问题时，就不得不提一下来自以利亚的芝诺。你听说过他讲的阿基里斯和乌龟赛跑的故事吗？阿基里斯自然比乌龟跑得快，所以乌龟被放在阿基里斯前方很远处起跑。随着发令枪响，阿基里斯的第一个目标是到达乌龟的起跑点。当然，到那时乌龟肯定已经往前爬了一小段路了。所以现在阿基里斯必须跑到乌龟目前所处的那个地点。等他到那里时，乌龟又爬到前面去了。不管阿基里斯到达乌龟之前所处的那个位置多少次（即使他尝试无数次），他永远都追不上乌龟，尽管他和乌龟之间的距离能够无限缩短。而乌龟只需要不停地向前爬就能赢得比赛。

类似的，还有跑道悖论。

为了到达跑道终点，参赛者首先就得跑完无数段路程。他必须先到达跑道中点，再到达剩下距离的中点，接着到达依然剩下的距离的中点，以此类推。从理论上来说，由于他不得不到达无数个中点，所以他永远不可能到达跑道终点。显然事实并非如此。这一点就连芝诺都能看出来。

下面是一则经典笑话，简直就像从芝诺嘴里讲出来的：

售货员：“女士，这款吸尘器能让您的工作量减少一半。”

顾客：“太棒了！给我来两台！”

这则笑话有点古怪。跑道悖论违背常识，所以即使我们搞不清楚到底哪里出了问题，我们依然会肯定某个地方出了问题。然而在这则吸尘器笑话里，芝诺的推理一点都不矛盾。如果这位女士的目的是不花任何时间就做完家务，那么没有哪种省时的吸尘器（或者和她同时操作吸尘器的人）能胜任该任务。同时使用两台吸尘器只会将清理地毯的时间缩短3/4，同时使用三台则缩短5/6，随着吸尘器数量的无限增加以此类推。

（摘自《柏拉图和鸭嘴兽一起去酒吧》，北京联合出版公司）