改进灰色神经网络导航在无人机巡线中的应用

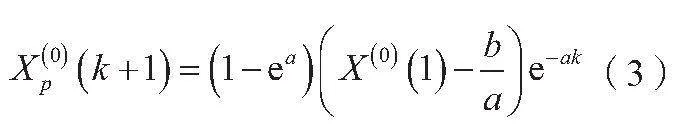
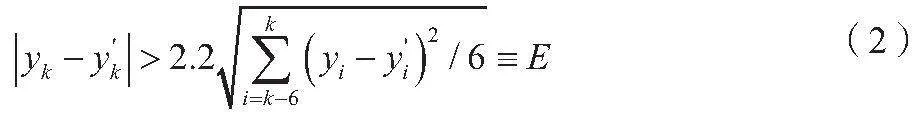
摘 要：为了消除无人机导航系统的误差，本文设计了改进灰色神经网络GNSS/SINS无人机电力巡线导航系统，基于Kalman算法对GNSS和SINS这2种导航数据进行融合。在GNSS信号缺失的情况下，改进灰色神经网络来预测缺失部分的数据，再结合SINS的数据对无人机的位置进行精准预测。算法设计完成后，运用MATLAB软件模拟验证系统算法的功能。结果显示，其位置预测数据精度良好，证明该系统能够提升无人机的导航效果。

关键词：GNSS/SINS组合导航系统；改进灰色神经网络；无人机电力巡线

中图分类号：TN 967" " " 文献标志码：A

全球导航卫星系统（Global Navigation Satellite System，GNSS）和捷联惯导系统（Strapdown Inertial Navigation System，SINS）是电力巡线无人机的主要导航方式，GNSS导航精度高，但是容易受到复杂地形和电磁因素的干扰，导致信号缺失；SINS导航精度较差，但是几乎不受其他因素影响。整合以上2种导航方式，能够弥补各自的缺陷，进一步提高导航精度。本文针对GNSS容易出现数据间歇性缺失的问题，创新性地引入改进灰色神经网络模型，预测缺失部分的数据，建立GNSS/SINS组合导航技术，显著降低无人机的导航误差。

1 GNSS/SINS无人机电力巡线导航系统设计

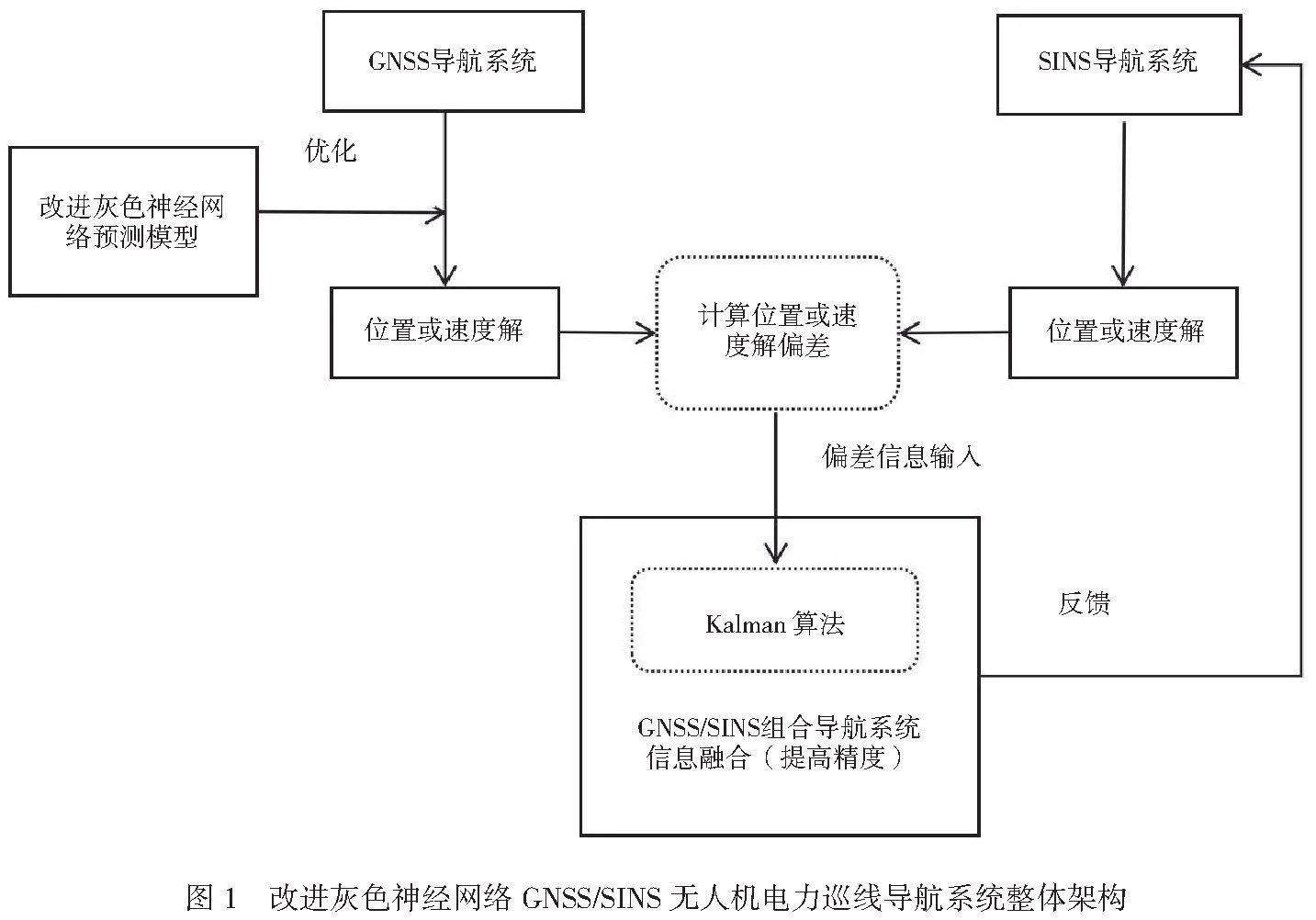
1.1 导航系统整体架构

无人机电力巡线作业系统主要采用2种导航定位技术，分别为GNSS和SINS。GNSS导航系统能够为无人机提供长时间、大范围的导航服务。SINS导航系统无须依赖外部系统，能够自主完成导航任务。这2类导航系统各自存在一定的局限性，GNSS受到山地复杂环境的干扰，容易出现信号中断的情况[1]。SINS导航精度较差，误差会不断累积。

本文设计的改进灰色神经网络GNSS/SINS无人机电力巡线导航系统对GNSS和SINS进行整合，利用算法工具提高整体的导航精度，整体架构如图1所示。

1.2 基于改进灰色神经网络模型的GNSS导航优化

在无人机电力巡线过程中，GNSS导航系统受到复杂环境干扰，有可能出现短时信号缺失的情况，导致GNSS/SINS组合导航系统不能进行信息融合。在这个情况下，可以改进灰色神经网络模型预测缺失的信号，保证后续信息融合模块正常运行。

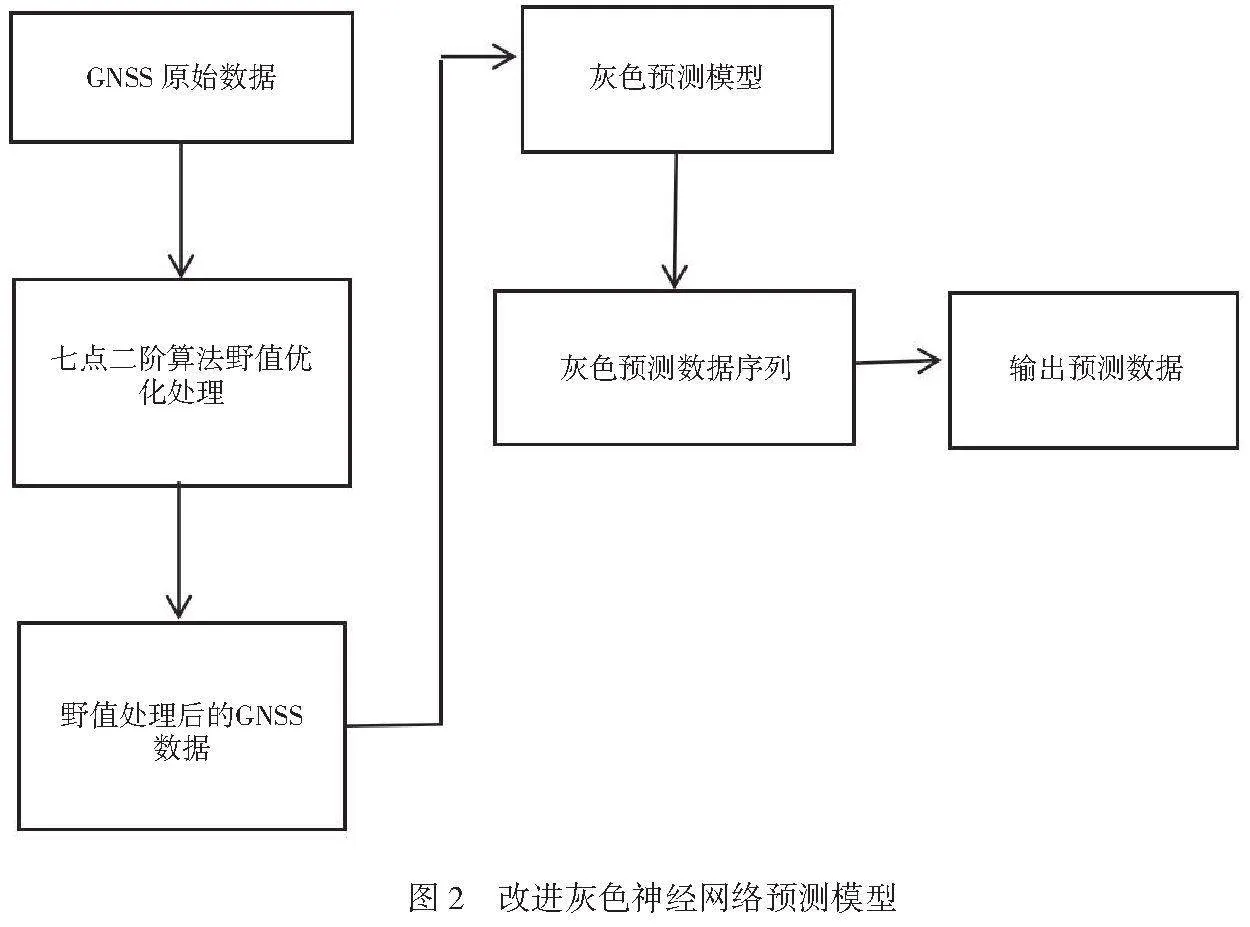
1.2.1 改进灰色神经网络预测模型整体架构

改进灰色神经网络预测模型融合七点二阶算法和灰色预测模型（Grey Models，GM）。GNSS系统利用接收天线采集原始数据后，根据七点二阶算法处理原始数据，再使用改进灰色神经网络预测模型进行缺失数据预测，模型如图2所示。

1.2.2 改进灰色神经网络预测模型设计

1.2.2.1 基于七点二阶算法的野值优化

野值是GNSS原始数据中的离散值，其特点为明显偏离正常范围，野值的存在降低了原始数据的平滑性和预测模型的精度[2]。基于此，利用七点二阶算法对原始数据进行处理，剔除原始数据中的离散值，增强原始数据的平滑性，提升模型的预测精度，该算法判断野值的步骤如下。

将GNSS系统采集的原始数据记为yi，i=7，8，...，n。i初始取值为7，原始数据中的前6项分别为yi-6、yi-5、yi-4、yi-3、yi-2和yi-1。采用七点二阶算法对原数据进行插值处理，如公式（1）所示。

yi'=（5yi-6-3yi-5-6yi-4+3yi-2+15yi-1+32yi）/42" （1）

式中：yi'为yi对应的插值。

野值的判断条件如公式（2）所示。

式中：yk为第k个采样时刻或数据点的观测值，由于i=k-6，因此yk对应原始数据集中的yi+6；yk'为yk对应的插值处理结果；k为当前处理的数据点的位置或时间步；i为索引，其作用是表示迭代或循环过程中的不同位置；yi为在特定范围内第i个数据点的观测值；yi'为该观测值的映射；E为辨识常数。当yk满足公式（2）时，属于野值，应该予以剔除。

1.2.2.2 基于灰色预测模型获取灰色预测数据序列

GNSS系统的原始数据有可能出现缺失，可以根据前期获得的数据预测缺失的部分。将野值处理后的GNSS原始数据输入灰色预测模型中，利用累加生成操作（Accumulated Generating Operation，AGO）进行预测，获取灰色预测数据序列[3]。

将输入灰色预测模型的原始数据集记为X（0），X（0）={X（0） （1），X（0） （2），...，X（0） （n）}，X（0） （n）为集合X（0）中的元素。根据灰色预测模型的相关原理计算X（0）的预测序列，如公式（3）所示。

式中：Xp（0）（k+1）为预测值，k=1，2，3，...，n。将k代入公式（3），得到对应的预测数据序列。a为发展系数；b为灰作用量。

1.3 基于Kalman算法的GNSS/SINS导航信息融合

由GNSS/SINS组合导航系统的工作原理可知，GNSS导航系统和SINS导航系统均可以产生无人机的位置解和速度解，但是2种导航系统的输出结果通常存在一定偏差。基于改进灰色神经网络的GNSS/SINS无人机电力巡线导航系统可以对2类系统输出结果进行融合，提升导航精度。信息融合方法如下。

1.3.1 SINS导航系统误差

Kalman滤波算法能够根据输入数据估算系统的最佳运行状态。将GNSS导航系统与SINS导航系统输出结果的差值输入Kalman滤波算法程序中，根据算法程序对数据进行融合处理，提升组合系统的导航精度。当预测系统状态时，该算法须利用SINS导航系统的误差构建GNSS/SINS组合导航系统的状态转移方程。

SINS解算机械编排获取载体的位置坐标，受到传感器和机械编排的影响，SINS系统有可能出现误差。将系统导航坐标与实际导航坐标之间的失准角向量记为φ，φ=[φN" φE" φD]T，其中φN、φE和φD为NED坐标系中N轴、E轴和D轴对应的失准角分量[4]。根据失准角构建实际姿态矩阵和理想无误差姿态矩阵的方程，两侧同时进行微分，计算失准角的误差方程，如公式（4）所示。

φ'=-ωn in×φ+δωn in-Cbnδωb ib （4）

式中：φ'为含误差的失准角；ωn in为惯性坐标系i相对导航坐标系n的转动角速度在n系中的矢量；δ为实际物理量与理想物理量之间的误差；Cbn为无误差情况下的导航系统姿态矩阵；ωb ib为SINS系统陀螺仪输出的角速度。对系统计算速度和理想速度的方程进行微分，得到无人机的速度误差方程，如公式（5）所示 [5]。

δvn=Cbnδf b+Cbnf b·φ-（2ωien+ωn en）·δvn+vn×（2δωn ie+δωn en）+δgIn

（5）

式中：vn为理想情况无人机相对地面的速度；δvn为速度误差；f b为惯性导航中的加表零偏；δf b为加表零偏误差量；ωn ie为地球自转角速度在导航坐标系中的分量；ωn en为导航坐标系n相对地心地固坐标系e的转动角速度在n系中的矢量；gIn为导航系统中的重力参数。采用相同的方法对无人机高程、纬度和经度进行分析，得到相应的误差方程。以高程为例，其对应的误差方程为δh=-δvD，h为理想高程参数，δh为包括误差的高程；vD为NED坐标系中D轴（垂直于地球表面的坐标轴）的速度。

1.3.2 基于SINS误差的组合导航系统Kalman算法状态方程

在第1.3.1节中，对SINS导航系统的误差分量进行分离，包括失准角、速度、高程、纬度和经度，其中纬度、经度和高程体现了无人飞行器的位置。以SINS误差为基础，根据Kalman算法建立GNSS/SINS组合导航系统的状态方程，如公式（6）所示。

式中：δ为误差系数；δr'n为Kalman算法修正后的位置误差矩阵；δv'n为Kalman算法修正后速度误差矩阵；φ'、bg'、ba'、r'n和v'n为参数φ、bg、ba、rn和vn经过Kalman算法滤波处理后的结果；F为系统状态矩阵；rn为无人机在导航坐标中的位置矩阵；δrn为位置误差矩阵；vn为理想情况下无人机相对地面的速度矩阵；δvn为速度误差矩阵；bg为陀螺仪的零偏误差；ba为加速度计的零偏误差；G为过程噪声矩阵；w为高斯白噪声向量。

1.3.3 GNSS位置更新

GNSS/SINS组合导航系统需要对GNSS和SINS各自的定位解算结果进行融合，但是2种导航系统的定位解算结果存在差异，前者为GNSS天线的位置，后者为惯性测量单元（IMU）的位置[6]。因此，当融合2种解算结果时，需要修正定位目标不同产生的误差。

GNSS天线与惯性测量单元的位置关系如公式（7）所示。

rn GNSS=rn IMU+D-1 RCbnl b GNSS " " " " " " " " " " " " " " " " " " " " " " " " " " " "（7）

式中：rn GNSS为导航坐标系中GNSS天线相位中心的位置矢量；rn IMU为惯性测量单元中心的位置矢量；D-1 R为位置修正矩阵；lb GNSS为杆臂的位置矢量。在GNSS信号缺失的情况下，利用公式（7）更新GNSS天线中心位置。

2 GNSS/SINS无人机电力巡线导航系统验证

2.1 仿真试验设计

2.1.1 试验目标

由上文可知，改进灰色神经网络GNSS/SINS无人机电力巡线导航系统的设计重点为野值处理、基于改进灰色神经网络的GNSS缺失数据预测、GNSS/SINS组合导航信息融合以及导航信息预测，试验目标为验证以上3个核心功能。

2.1.2 电力巡线场景选取

无人机电力巡线的场景比较复杂，包括平原、丘陵和山地等。在真实场景中，丘陵、山地复杂的地势、多样的植被会形成干扰，容易导致GNSS信号缺失。为了验证导航算法对野值的处理效果和对缺失数据的预测效果，选取丘陵山地场景。

2.1.3 仿真方法以及参数设置

本文利用MATLAB搭建仿真环境，设置无人机的初始飞行速度，使其在特定高度进行周期性飞行。模拟开始后，当采集导航定位数据时，在9 s、45 s插入离散值（野值）。GNSS导航系统在50 s～65 s出现信号缺失的情况。其他仿真参数见表1。

2.2 仿真数据分析

2.2.1 野值处理仿真数据分析

野值处理的目标是准确识别、剔除超过正常范围的离散值，野值出现的时间点为仿真开始后的9 s和45 s，利用七点二阶算法进行处理，从速度和位置2个方面评价野值处理的效果。

2.2.1.1 基于无人机速度的野值处理效果分析

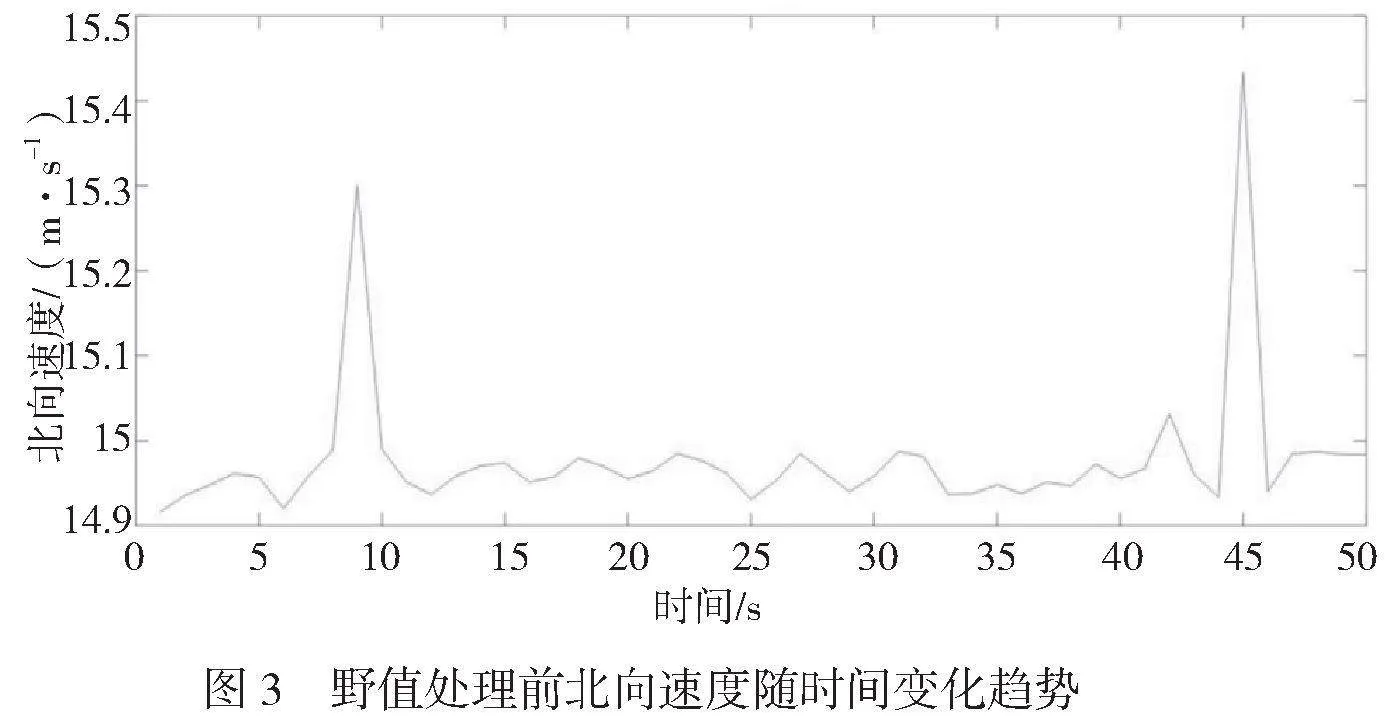
在野值处理前，北向和东向的速度在9 s和45 s出现了明显的离散点。以北向速度为例，其变化趋势如图3所示。在0～50 s，正常速度约为14.9 m/s～15.0 m/s，2个野值分别为15.3 m/s、15.4 m/s。经过处理后，0～50 s的北向速度为

14.9 m/s～15.0 m/s，东向速度的2个野值为14.6 m/s、14.9 m/s。经过处理后，0～50 s的速度为14.15 m/s～14.30 m/s。说明七点二阶算法对速度野值的处理效果良好。

2.2.1.2 基于无人机位置的野值处理效果分析

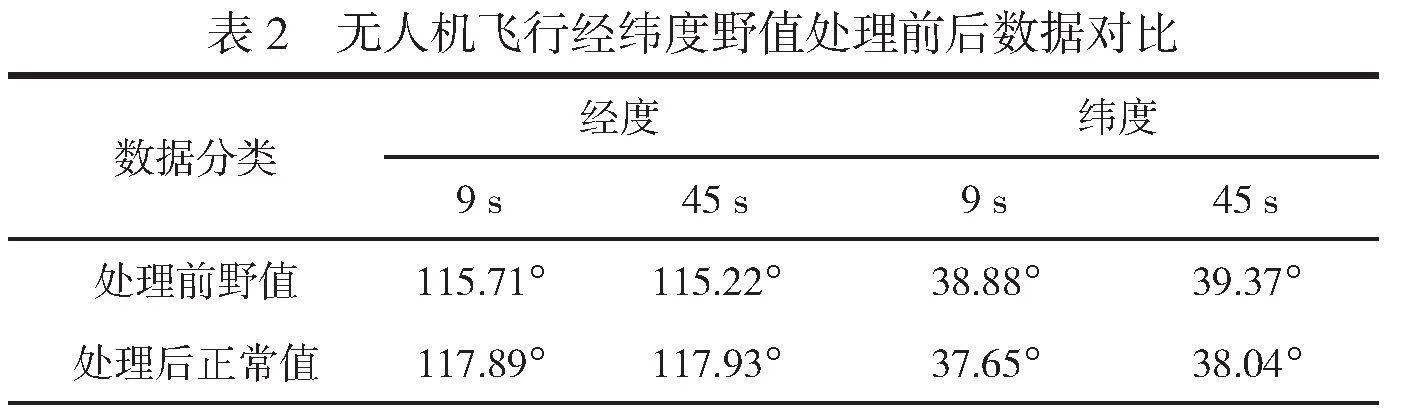
经度和纬度数据能够体现无人机的位置，对处理前后的经纬度野值数据进行对比，得到的结果见表2。由表2可知，经过七点二阶算法优化，野值明显下降，回落至正常范围。

2.2.2 改进灰色神经网络对GNSS缺失数据预测效果分析

将传统灰色神经网络和改进灰色神经网络作为对照组，以0～50 s采集的正常数据为依据，利用2种算法对50 s～65 s缺失的数据进行预测，包括北向速度、东向速度、经度以及纬度，效果对比见表3。由表3可知，利用改进灰色神经网络预测缺失的GNSS数据，其平均误差、均方误差和最大误差均小于传统灰色神经网络，预测精度更高。

2.2.3 基于GNSS/SINS组合导航的无人机位置预测

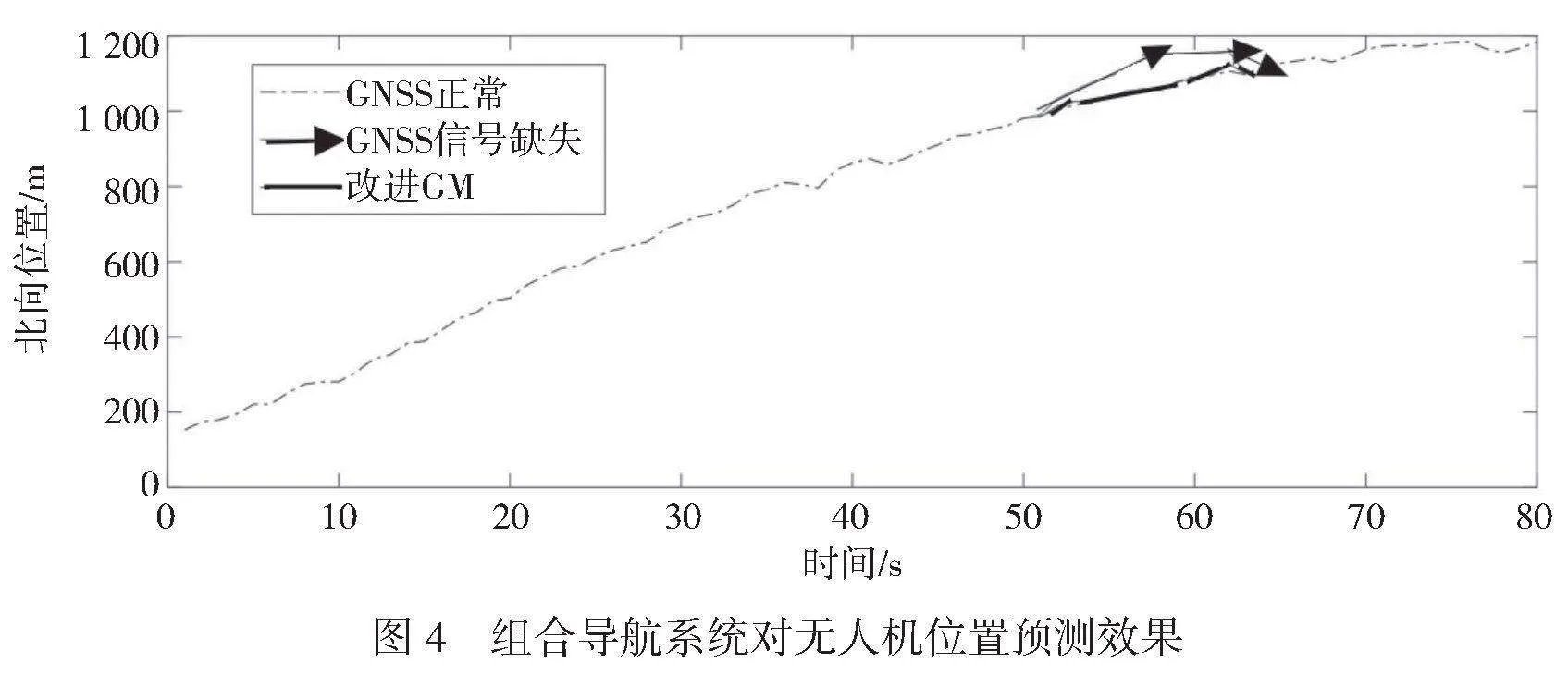
将SINS数据和GNSS数据进行融合，能够进一步提高系统对无人机位置的预测精度，消除导航误差。利用改进灰色神经网络GNSS/SINS组合导航系统模拟位置预测效果，模拟结果如图4所示。其中，虚线为GNSS未缺失的正常数据，箭头线为GNSS信号缺失、仅依靠SINS进行导航的数据，实线为改进灰色神经网络GNSS/SINS组合导航系统的位置预测数据（改进GM）。组合导航系统的预测结果与正常的GNSS数据高度一致，位置精度预测效果良好。

3 结论

针对无人机GNSS导航容易出现数据缺失、SINS导航精度较差的问题，本文设计了改进灰色神经网络GNSS/SINS组合导航系统，得到以下结论。1）由于GNSS导航系统容易受到电磁信号或者复杂地形干扰，导致部分位置、速度数据缺失，不能提供可靠的导航，因此本文设计改进灰色神经网络模型，预测缺失部分的数据。模型采用七点二阶算法处理异常的离散值，提升数据的平滑性，并运用灰色神经网络进行预测。进行仿真测试，测试结果表明其预测精度较高。2）使用传统的GNSS/SINS组合导航方式，如果GNSS数据缺失，仅由SINS进行导航，那么误差会较大。改进灰色神经网络GNSS/SINS组合导航系统采用Kalman算法融合SINS数据和预测的GNSS数据，能够显著提升无人机的位置预测精度，进行精准导航。

参考文献

[1]杨春峰，于荣华，黄维，等.基于激光雷达和可见光立体测量的无人机电力巡线技术研究[J].自动化技术与应用，2021，40（10）：177-180.

[2]郭迟，陈毅超，罗亚荣.一种世界坐标系下的GNSS/SINS松组合导航矩阵李群滤波算法[J].中国惯性技术学报，2024，32（3）：242-249.

[3]王兆辉.基于数据融合的电力线巡检无人机安全距离研究[J].机械设计与制造工程，2022，51（11）：53-56.

[4]王玮，潘新龙，林雪原，等.GNSS/SINS组合导航系统的改进变分贝叶斯自适应滤波算法[J].大地测量与地球动力学，2024，44（6）：560-565.

[5]吴嘉琦，冉术兰.输电线路巡线中的无人机技术应用[J].电子技术，2023，52（9）：242-243.

[6]陈广宇，张磊，赵磊，等.基于改进神经网络的电网线损率预测模型分析[J].自动化技术与应用，2022，41（5）：130-133.