基于Python的加权K-means聚类算法研究

摘 要：本文针对K均值聚类算法在现实问题中的复杂性提出一种加权的聚类算法。K-means算法是一种经典的聚类算法，针对这种算法中的问题，目前有很多处理方法，例如确定初始聚类数K值、选择初始聚类中心点、数据点的权重影响以及孤立点的处理方式等。在实际问题中，坐标数据点的权重不同，本文将权值附加在数据点中，再使用肘部法则计算聚类数K值的最佳选择，分析数据点归属的簇。在数据集中进行比较，试验结果表明，与原算法相比，本文算法更接近实际数据分布，轮廓系数更接近1，聚类效果更好。

关键词：加权K-means算法；肘部法则；轮廓系数

中图分类号：TP 312" " " " " " 文献标志码：A

21世纪是信息时代，大量数据利用聚类算法挖掘有效的信息，聚类算法在各个方面得到了新的发展。例如其与深度学习结合，利用深度学习来提高聚类性能，成为无监督学习领域的研究热点。再例如其与图像识别领域结合，有研究提出一种基于余弦定理和K-means的识别方法[1]。将聚类算法应用于大规模数据集，探索在串行计算环境中基于样例选择、增量学习、特征子集和特征转换的聚类算法[2]。K-means算法在确定算法中聚类数目 K值、初始聚类中心选取、离群点的检测与去除以及距离与相似性度量等方面有一定的局限性[3]。针对初始点问题，可以使用粒子群优化（Particle Swarm Optimization，PSO）算法，收敛速度较快[4]。在全局搜索能力提升的基础上，优化局部搜索策略，使其在进化过程中始终保持勘探能力最佳[5]。基于密度算法优化初始聚类中心，这种方法能够优化聚类结果[6]，根据距离和的思想消除聚类分析结果中的孤立点的影响[7-8]。

1 相关概念介绍

1.1 K-means聚类算法

K-means算法是一种基于划分的无监督学习的聚类算法，采用欧式距离作为衡量数据对象间相似度的指标，相似度与数据对象间的距离成反比，相似度越大，距离越小。K-means算法预定义K的值[4]，指定K个初始聚类中心，并将给定数据集划分为K个簇，经过多次迭代不断降低类簇的误差平方和（Sum of Squared Error，SSE），最小化簇内平方和（Within-Cluster Sum of Squares，WCSS），当簇中心点以及数据所属簇趋于稳定时，聚类结束，得到最终结果。

给定一个数据集X={x1，x2，...，xn}，每个xi属于d维空间，预定义簇的数量 K，K-means的作用是找到使以下目标函数最小化的簇中心μ={μ1，μ2，...，μK}，如公式（1）所示。

数据点至其所属簇的中心点的距离的平方和，其值越小，聚类效果越好。

该算法计算数据集中每个数据点至所有初始数据中心的距离的最小值，将其分配至最近的中心点所属的簇中，并不断更新簇中心点的坐标，迭代计算数据点所属的新簇，直至算法收敛为止，将数据分割为误差平方和最小的K个簇。

1.2 加权K-means聚类算法

在传统的K-means聚类算法中，每个数据点对聚类的贡献都是相同的。但是，在实际问题中，有许多要素对数据点有加成或削弱作用。为了解决这个问题，采用数据点加权的聚类算法。一种常见的加权聚类算法是加权K-means算法，这种加权距离能够同时捕捉数据点之间的全局空间关联和局部变化趋势。在这个算法中[9]，每个目标数据点都赋予1个权值，这个权值反映了数据点在聚类过程中的重要程度，将权值附加在计算K-means算法过程中，得到更具有代表性的聚类结果。

具体来说，假设数据点X={x1，x2，...，xn}，每个点xi都有一个相应的权重wi，那么加权K-means算法的目标函数如公式（2）所示。

加权K-means算法的基本步骤如下。输入：数据集为X，数据点权重为W，预定义的簇数量为K。输出：簇中心为μ，数据点所属簇为C。

采用加权 K-means 算法可以有效地将数据点分配至最佳的簇中。该算法有以下5个核心步骤。1）随机选择K个点作为初始簇中心μ0。2）计算数据集X中的每个数据点xi至每个簇中心点μi的加权距离，将该数据点分配至与其加权距离最短的簇中心点所对应的簇Ci。3）计算每个簇Ci中所有数据点的加权平均值，将其作为新的簇中心点μi。4）重复步骤2、3，直至目标函数G不再变化，算法收敛。5）输出结果，返回簇中心μ和数据集中所有数据点所属簇C。

加权聚类算法在计算过程中考虑了数据点差异性，提高了聚类结果的准确性和可信度，在实际生产中应用前景广阔。

1.3 肘部法则

在聚类算法中，确定簇的个数K值是一个重要的研究方向。常用的方法包括经验法则、肘部法则和轮廓系数等。经验法则是基于经验或知识来确定个数的一种常用方法，在准确性要求不高的情景中可以采用。当使用加权聚类算法时，将每个数据点按照重要程度赋予不同的权值，问题分析的纬度更多，对K的确定要求更高，因此肘部法则是一个很好的选择。

在通常情况下，随着K值递增，WWCSS会逐渐降低，当到达某一点后，误差幅度会显著降低，出现1个肘部拐点，整条曲线呈现为肘部形状。这个肘部对应的点的K值即最佳K值。在后续加权聚类算法中，根据K值进行计算，得到的聚类效果最好，呈现的簇的区分最明显，也更符合实际情况。

使用肘部法则确定的合理 K值不仅可以保持聚类精度，而且可以降低算法的复杂度，为加权聚类算法的应用提供重要的指导。

2 试验结果和分析

本文将传统K-means算法应用于实际聚类问题中，将数据点用特征值进行加权，分析聚类效果。本文采用的测试数据集是Yelp平台在美国宾夕法尼亚州所有餐厅的数据。在数据集中共有514条餐厅数据，每条数据包括餐厅的15个属性信息：'business_id'， 'name'，'neighborhood'，'address'， 'city'，'state'，'postal_code'，'latitude'，'longitude'，'stars'，'review_count'，'is_open'，'attributes'，'categories'，'hours'。其中星级评价分为1～5级，由用户给出，该评价是1个餐厅非常重要的信息，决定后根据餐厅星级，用户是否会去这个餐厅就餐，因此可以将这个参数作为每行数据的权重。计算这个地区哪个范围内的餐厅密度最高，基于城市聚集效应，以此作为推荐后续新餐厅的选址依据。为解决这个问题，采用K-means算法计算坐标点的聚类结果，并比较传统K-means算法与加权聚类算法在聚类效果方面的差异，本文主要比较轮廓系数的值。

当比较2个聚类方法的问题时，通常比较2个算法的聚类误差，误差越小，聚类效果越好。但是本文比较的是加权聚类和传统聚类的聚类效果，在加权的情况下考虑了每个数据点的权重，自然加权聚类误差的WWCSS应该大于传统聚类误差的WCSS，因此，比较2种聚类的轮廓系数（Silhouette Coefficient）来判断效果。轮廓系数是一种常用的聚类效果评估指标，其作用是衡量聚类的紧密度和分离度。轮廓系数的取值范围为[-1，1]，其值越接近1，聚类效果越好；其值越接近-1，聚类效果越差，值接近0表示聚类效果不明显。基于传统K-means算法，采用肘部法则计算这514个数据的聚类数K值，数据点使用'latitude'，'longitude'这2个参数作图，聚类数K值与WCSS的变化曲线如图1所示。

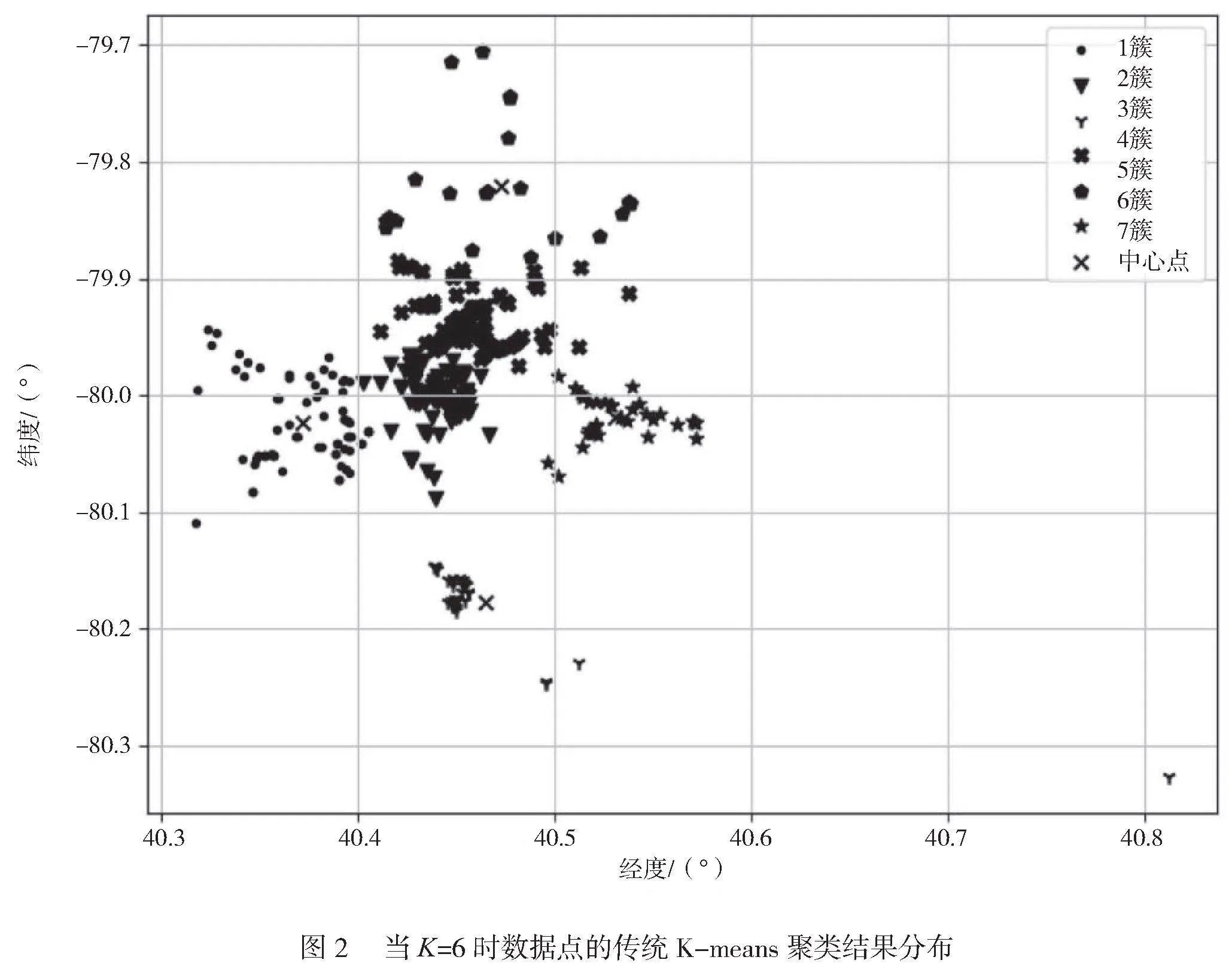
由图1可知，曲线肘部的取值为k=6，即当聚类数为6时，聚类的效果最好。当聚类数K=6时，测试集中数据点的聚类结果分布如图2所示。

由图2可知，Cluster 的数据点最多，当经纬度为[40.40～40.47， -80.11～-79.94]时，可以作为后续新餐厅的选址推荐。在传统K-means算法中，WCSS为0.632，轮廓系数为0.518。

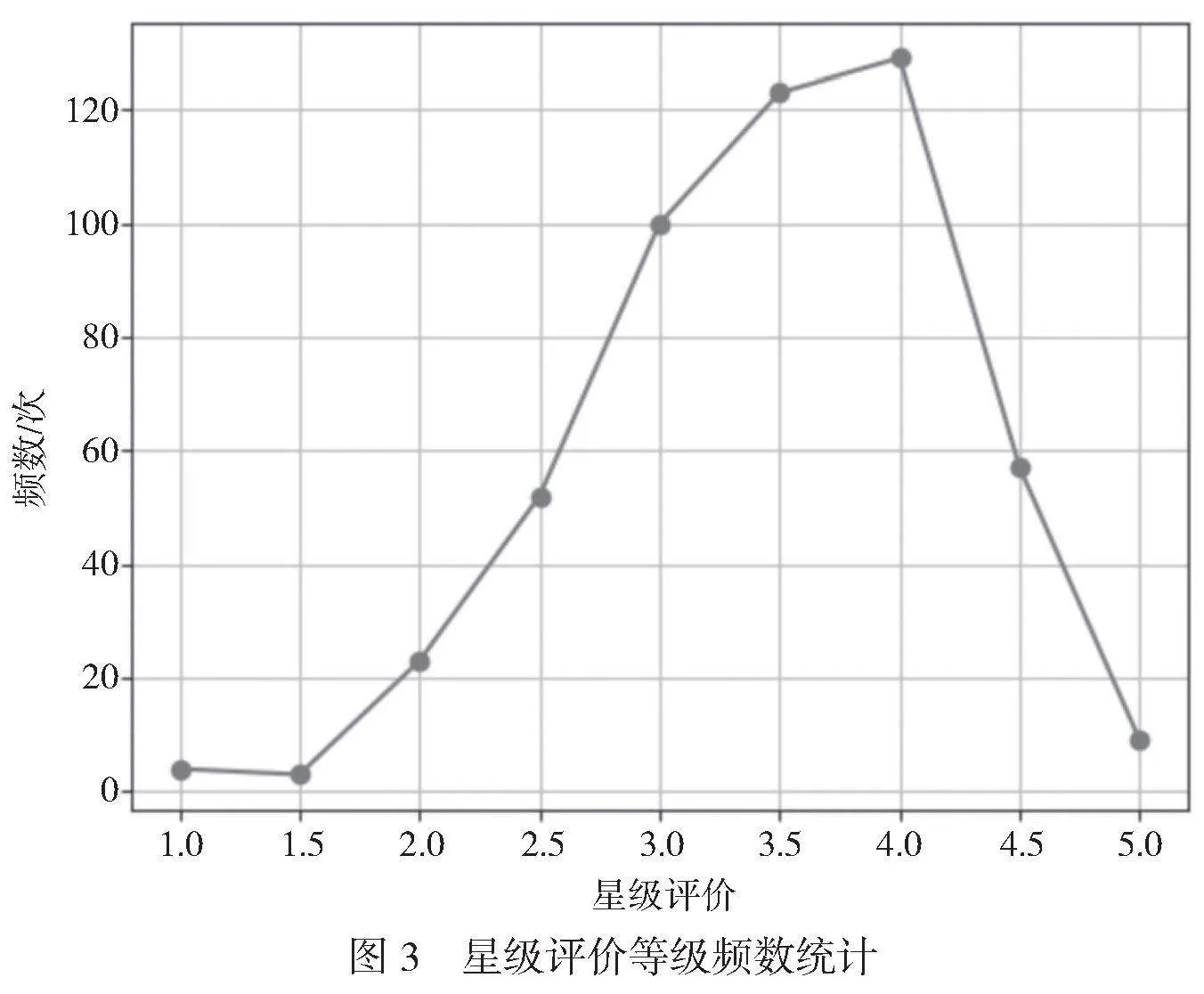
基于加权K-means算法，先统计测试集中每个数据点的权重分布情况，星级评价等级频数统计如图3所示。利用肘部法则计算这些数据的最佳聚类数K值。

餐厅星级评价等级为1～5。由图3可知，顾客星级评价等级主要集中在3.0、3.5和4.0，等级两端的出现频率最低。也就是说514个数据点的权值分布在1～5的离散数中，3.0、3.4和4.0的出现频率最高。

采用肘部法则计算这514个数据当使用加权聚类算法时的最佳K值，K值与WWCSS的变化曲线如图4所示。其中横坐标为聚类数K的值，纵坐标为加权的WWCSS。

由图4可知，拐点在7。当数据集簇的个数定位7时，WWCSS的下降趋势有了明显的变化，即K值确定。测试集中数据点的加权聚类结果分布如图5所示。

由图5可知，Cluster2的数据点最多，当经纬度为[40.41～40.54，-79.98～-79.88]时餐厅的密集度最高，可以作为后续新餐厅的选址推荐。在加权K-means算法中，WWCSS为1.669，轮廓系数为0.523。

3 结论

本文采用特征值加权的聚类方法处理坐标数据点，将聚类问题应用于复杂因素影响的数据集中。使用肘部法则确定最佳簇个数K值，最后完成数据点集合。与传统K-means算法得到的轮廓系数相比，加权K-means得到的轮廓系数更大，更接近1，因此聚类效果更好，更符合实际情况。在实际问题中，数据点的信息是复杂的，下一步的研究重点是基于多维度给数据点加权。

参考文献

[1]姬强，孙艳丰，胡永利，等.深度聚类算法研究综述[J].北京工业大学学报，2021，47（8）：912-924.

[2]朱颢东，申圳.基于余弦定理和K-means的植物叶片识别方法[J].华中师范大学学报（自然科学版），2014，48（5）：650-655.

[3]何玉林，黄哲学.大规模数据集聚类算法的研究进展[J].深圳大学学报（理工版），2019，36（1）：4-17.

[4]杨俊闯，赵超.K-means聚类算法研究综述[J].计算机工程与应用，2019，55（23）：7-14，63.

[5]刘靖明，韩丽川，侯立文.基于粒子群的K均值聚类算法[J].系统工程理论与实践，2005（6）：54-58.

[6]陶新民，徐晶，杨立标，等.一种改进的粒子群和K均值混合聚类算法[J].电子与信息学报，2010，32（1）：92-97.

[7]傅德胜，周辰.基于密度的改进K均值算法及实现[J].计算机应用，2011，31（2）：432-434.

[8]周爱武，于亚飞.K-Means聚类算法的研究[J].计算机技术与发展，2011，21（2）：62-65.

[9]NING" Z" L，CHEN" J，HUANG" J" J ，et al.WeDIV -An improved"k-means clustering algorithm with a weighted distance and a novel"internal validation index[J].Egyptian Informatics Journal，2022，23（4）：133-144.