改进遗传算法求解柔性作业车间调度问题

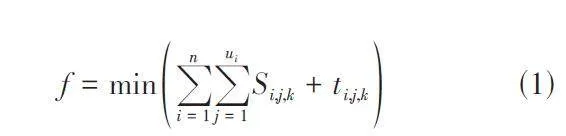
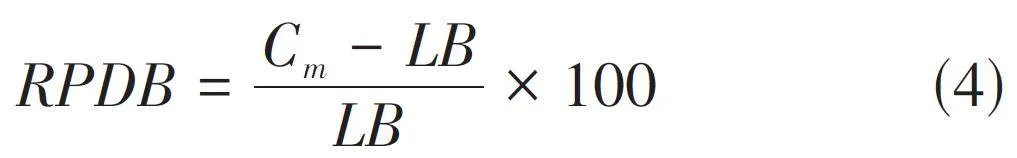
摘要：为优化生产要素配置提高资源利用率，构建了以最小化最大完工时间为目标的调度模型，提出了一种自调整搜索域的改进遗传算法求解柔性作业车间调度问题（Flexible Job-shop Scheduling Problem， FJSP） 。算法采用基于工序排列和机器选择的双层染色体编码的设计方案。设计了新的种群初始化方法，在交叉和变异阶段，引入自适应参数，优化遗传操作流程。在进化后期引入新种群增加染色体的多样性，自调整算法搜索域，帮助种群跳出局部最优，找到更好的全局解。实验结果表明提出的改进遗传算法在优化精度和收敛能力方面表现良好。

关键词：作业车间调度；柔性；遗传算法；自调整搜索域；染色体多样性

中图分类号：TP18;TH165 文献标识码：A

文章编号：1009-3044（2024）27-0079-04

0 引言

柔性作业车间调度问题（Flexible Job-shop Sched⁃uling Problem， FJSP） 是作业车间调度问题（Job-shopScheduling Problem，JSP） 模型的扩展[1]，更紧密地贴合了现实生产场景[2]。FJSP赋予了在机器选择上的更大自由度，能够应对涉及众多机器、多重工序及任务的复杂调度需求[3]，从而更好地适应多变且复杂的生产环境，也因此备受学界及业界的关注。

通过国内外学者的深入探索，智能优化算法在处理FJSP时显示出比传统方法更强的适应性和灵活性。特别是面对大型复杂的FJSP时，智能优化算法展现出了卓越的性能，能够在广阔的解空间中迅速锁定全局最优解，优化资源的使用效率。龙等人[4] 通过结合强化学习算法，强化了人工蜂群算法的全局搜索能力和收敛精确性。贾等人[5]提出了一种改进的粒子群优化算法，通过自适应调整参数和采用混沌局部优化器，显著提升搜索精确性和收敛速度。李星宇等[6]提出了一种创新的混合算法，该算法融合了遗传算法和禁忌搜索两种策略来求解，在实现全局寻优的同时，也能进行精细的局部调整。邢丽玲等[7]提出了一种基于知识的蚁群优化求解FJSP。此模型从蚁群优化中学习，并将获得的知识应用到当前的搜索过程中。张国辉[8]提出了一种混合粒子群和禁忌搜索来解决包含多个冲突和不可通约因素的FJSP，算法在处理复杂、多冲突的FJSP时表现出更高的效率和准确性。

遗传算法（Genetic Algorithm，GA） 作为智能优化算法的代表，在解决FJSP中展现出卓越的性能。GA基于候选解的种群，通过交叉、变异等遗传操作不断生成新的解决方案。此外，GA还具备强大的并行处理能力，能够同时优化多个目标，如机器配置、时间分配等，从而实现资源的高效利用和生产效率的提升。

本研究以遗传算法为核心，致力于以最小化最大完工时间为主要优化目标。提出了一种自调整搜索域的改进遗传算法（Self-adjusting Search Domain GA，SAGA）。通过深入探索求解FJSP的理论和方法，期望能够在实际生产环境中实现效率的提升，推动智能优化算法在生产调度领域的应用，为实际生产过程中的资源配置和效率提升提供有力支持。

1 问题描述

FJSP被定义为在具备多样化机器集群和不同类型工件的车间中，确定最优的工序顺序以及每道工序的执行机器的任务。具体数学模型描述为：一组相互独立数量为n 的工件（J1，J2，…，Jn） ，这些工件需要在m台不同的机器（M1，M2，…，Mm） 上进行加工处理。对于每个工件Ji，由u 个加工工序（u=1，2，…，3） 组成。每个加工步骤都需要一定的时间来完成，时间大于0，且每个步骤都至少可以在一台机器上完成。在任意给定的时刻，一台机器只能处理一个加工步骤，不能同时处理多个任务。此外，一旦一个加工步骤开始，必须直到完成加工，中间不能有中断。同时，不考虑工件在不同机器之间的运输时间。该调度模型的核心目标是实现所有加工步骤完成时间的最小化，可以通过以下的目标函数来表达：

其中，Si，j，k表示工序Oij在机器k 上加工开始时间。ti，j，k表示工序Oij在机器k 上所需加工时间。

2 算法设计

2.1 染色体表示

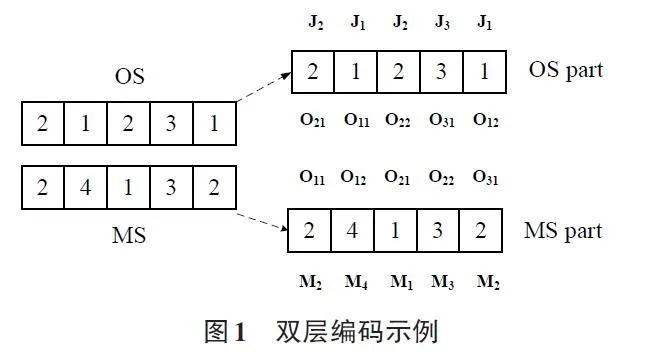
FJSP的关键在于处理两个核心子问题，即工序排列（Operation Sequence， OS） 和机器选择（Machine Selec⁃tion， MS） [9]，采用双层染色体表示法能够较好地解决这两个子问题。以图1为参考，在OS 部分中，首个数字“2”指代的是第二个作业的首个加工工序，标记为O21。接下来的数字“1”则代表第一个工件的第一个操作，表示为O11。当数字“2”再次出现时，它表示的是第二个作业的第二个步骤，记作O22。后续的数字遵循相同的编码规则，且染色体的长度与操作的总数相匹配。因此，操作序列“2-1-2-3-1”可以对应地解读操作序列：“ O21-O11-O22-O31-O12”。

与OS部分相似， MS部分的染色体长度等同于全部操作的总数量。以图1中的MS部分为例，若某个操作，如O22，对应位置的数字是3，表示选用第三台机器来执行此操作。具体可用的机器数量取决于具体问题的实际情况。因此在MS部分，每个数值都被特别设定为代表执行当前操作的机器编号。

2.2 种群初始化与进化算子

种群初始化是GA的关键一环。当前广泛采用的初始化MS部分策略是张国辉等[10]提出的全局与局部选择相结合的方法，本研究在MS部分也采用此策略。鉴于现有研究在OS部分的初始化方面缺乏完善方案，提出了一种优先选取剩余操作最多的工件法（Pri⁃oritize Selection of Most Remaining Operations，PSMRO） 为染色体的OS部分进行初始化：

（1） 设置一个记录每个工件被选中次数的数组，并将所有元素预设为0。

（2） 构建一个长度为n 的数组，其中每个元素代表各工件的操作数。

（3） 在上述创建的数组中，挑选出剩余操作最多的工件。若存在多个工件剩余操作数相同，则随机选取一个。

（4） 将所选工件的编号记录到步骤1中创建的数组里，并相应减少步骤2中数组对应位置的操作数。

（5） 不断重复步骤3和4，直至步骤2中数组的所有元素归零。

GA核心在于通过个体选择操作来模拟自然选择过程。在选择过程中，使用三元锦标赛进行选择，旨在从种群中筛选出表现优异的个体，并将其保留在基因库中。在经过一轮或多轮的繁衍后，这些优秀的个体可以为后续的进化过程提供高质量的遗传基因。

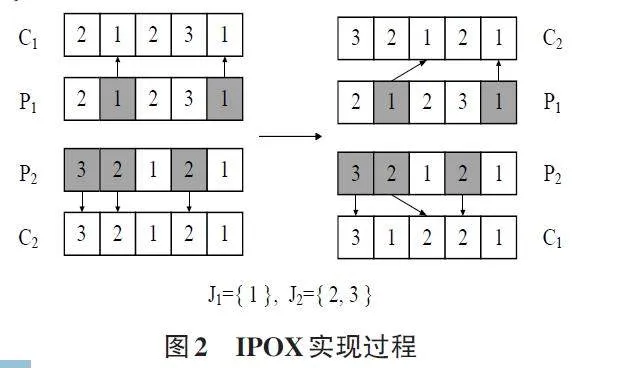
鉴于双层染色体结构特点，针对OS和MS部分分别实施了两种不同的交叉操作策略。在OS部分，采用了改进的优先顺序交叉（Improved Precedence OrderCrossover， IPOX） 方法。具体步骤为：首先，将作业集随机划分为J1和J2两个子集，并随机选择两条父代染色体P1和P2。接着，将P1中隶属于J1集合中的基因以及P2中隶属于J2集合的基因分别复制到子代个体C1和C2中，同时确保这些基因在C1和C2中的位置与原染色体保持一致。然后，依次从P1中复制属于J1集合的基因到C2中的空缺位置，从P2中复制属于J2集合的基因到C1的空缺位置，完成基因的交叉过程。如图2。

MS部分由一系列代表加工机器的元素构成，每个元素都对应一个具体的操作。在MS部分进行交叉操作时，涉及在染色体的两个不同点交换基因，从而创造出两个全新的MS序列。当两条染色体上的同一位置出现相同的数字时，这表明该位置的机器是可选机器集合中的一员。通过等位基因交叉产生的新染色体依然满足原有的约束条件，因此交叉操作后得到的新个体仍然是有效的解决方案[11]。本研究采用的是两点交叉法来进行这一操作。

为了避免算法过快地陷入局部最优解，需要引入变异操作。在染色体的OS部分，实行两点变异操作。而当MS部分发生变异时，从可用的机器集合中随机选取一台新的加工机器替换原有的机器，以增加种群的多样性。

2.3 搜索域自调整策略

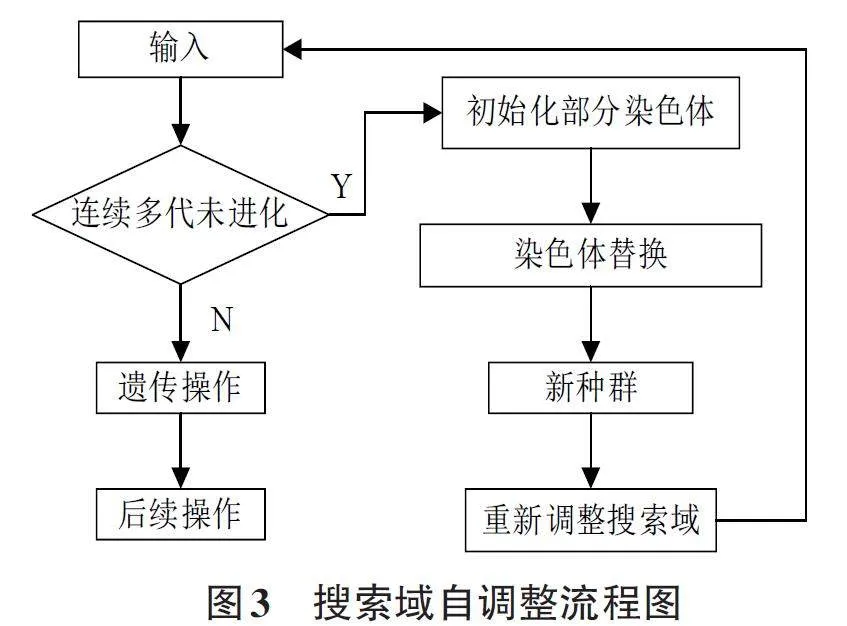
为了应对算法早熟收敛现象，采取了一种新策略，当算法检测到种群陷入局部最优时，初始化一小部分种群参与后续的进化过程中。这一策略通过生成全新的染色体，并随机替换除当前最优染色体外的相同数量的其他个体，以此来调整解空间的搜索范围，进而增强基因的多样性。引入新种群的频率根据当前的进化状况进行自适应调整，在搜索速度和搜索精度之间找到一个更好的平衡点。通过这种自适应机制，算法能够随着种群的进化自动调整其搜索范围，从而更有效地探索整个解空间。图3展示了染色体初始化的决策判定逻辑与操作步骤。

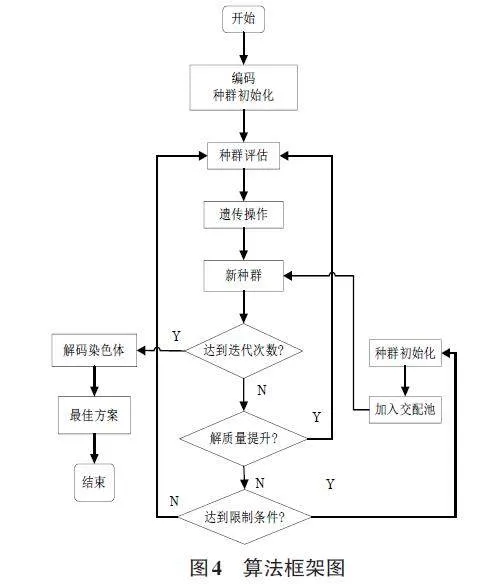
2.4 改进GA 的框架

基于前述讨论，构建了如图4所示的算法框架。

3 仿真实验及分析

本研究阐述的算法使用Matlab 2020a编写，实验环境为配置搭有Intel Core i5处理器、8GB内存的Win⁃dows 10操作系统。为验证算法的有效性，选用了两组广受认可的FJSP基准测试数据。其中一组是规模相对较小的Kacem 数据集[12]，另一组是更为复杂的Brandimarte数据集[13]。对于每个测试实例，都进行20 次的运行试验。算法种群数设置为5*m*n（m， n为实例规模），最大的迭代次数设为10*m*n，交叉变异概率动态自适应，公式如下：

Pc =-Ft - minFt／ maxFt - minFt （2）

Pm = minFt ／maxFt （3）

其中，-Ft 为平均适应度，minFt和maxFt分别为最小、最大适应度。

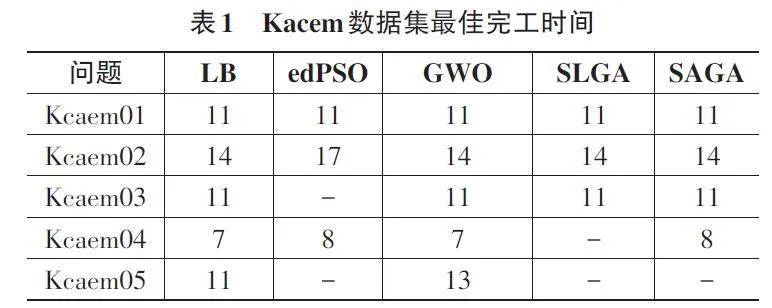
本节将SAGA与SLGA[14]、edPSO[15]、GWO[16]三种算法进行了比较，以评估SAGA的整体表现。表1展示了Kacem数据集上各算法的对比结果。由于未找到Kcaem05原始数据集，在剩余的四个实例中，SAGA在三个实例中都达到了问题实例的下界（LB） 结果。这一数据表明，在处理较小规模的问题时，SAGA算法拥有良好的性能和效果。

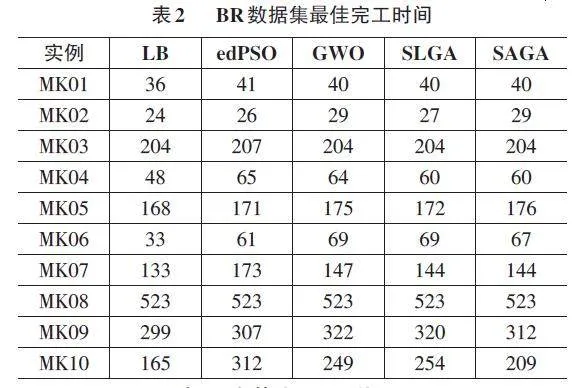
表2呈现了几种算法在中等至大规模的10个BR 数据集上的实验结果。由表中数据可以看出，SAGA、edPSO和SLGA均取得了 5次最优表现。尽管GWO 在Kacem数据集上表现出色，但在此次测试中，它仅在2个实例上达到最右。这些实验结果表明，SAGA 在处理大规模问题时展现出更高的适应性。

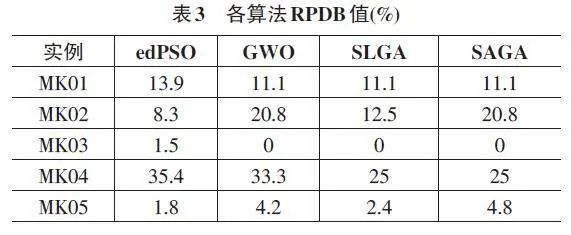
表3给出了按相对百分比偏差（RPDB） 衡量的比较结果。其计算式为：

根据表格数据，SAGA算法在MK01、03、04、08和MK10上找到最佳解。同时，在其余的三个实例中，按照RPDB的衡量标准，SAGA也取得了次优的结果。

修正RPD （CRPD） 是通过对算法求解结果与最优解或已知下界进行比较，进一步衡量算法性能的一种指标。具体的计算方法是，先求出算法求解结果与最优解（Best） 和下界的差值，再除以最优解或下界，最后将得到的比值乘以100，以此表示算法求解结果与理论值的偏差程度。公式如下：

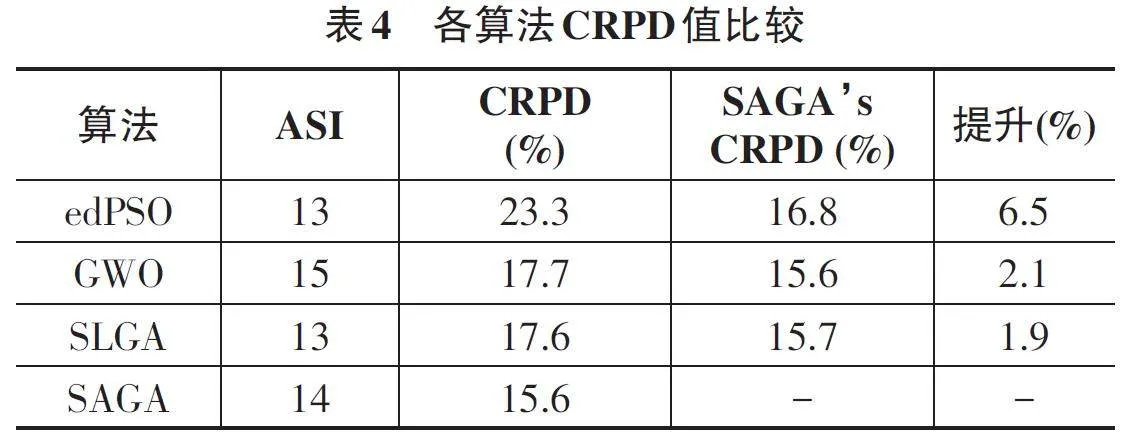
表4详细展示了所有参与比较的算法的实际求解数（ASI） 以及每种算法的修正相对百分比偏差（CRPD） 。在该表中，“提升”这一列特指SAGA算法相较于两组基准测试中的其他算法，在CRPD方面所取得的减少值。

从数据中可以明显看出，除了SLGA算法之外，SAGA 在CRPD 上均实现了不同程度的提升。尽管SAGA的CRPD相比SLGA只是略有优势，但这仍然显示了SAGA在优化FJSP的最大完工时间方面，表现出了更加卓越的性能和效率。

4 结论

为求解FJSP，提出了一种自调整搜索域的改进遗传算法（SAGA） 。采用双层基因链染色体表示方法独立地在操作序列和机器选择上进行遗传操作。同时，为了提高搜索效率，将提出的PSMRO方法应用于初始化操作顺序部分。当种群陷入局部最优时，部分种群被重新初始化，自调整搜索域，以提高染色体的多样性，丰富种群的基因库。

最后在选定的基准测试集上对SAGA进行了测试。实验验证发现SAGA在处理FJSP时展现出了良好的性能。本研究不仅为FJSP的求解提供了新的有效方法，还为实际生产调度中的优化问题提供了有价值的参考。

参考文献：

[1] 屠军权.智能制造时代机械设计制造及其自动化技术研究[J].工程施工新技术，2022，1（2）：153-155.

[2] 魏巍，谭建荣，冯毅雄，等.柔性工作车间调度问题的多目标优化方法研究[J]. 计算机集成制造系统，2009，15（8）：1592-1598.

[3] 余斌煌.柔性流水车间调度问题综述[J].现代制造工程，2022（9）：154-162，71.

[4] LONG X J，ZHANG J T，QI X，et al.A self-learning artificial bee colony algorithm based on reinforcement learning for a flexible job-shop scheduling problem[J].Concurrency and Computation：Practice and Experience，2022，34（4）：e6658.

[5] JIA Z H，CHEN H P，TANG J.An improved particle swarm opti⁃mization for multi-objective flexible job-shop scheduling prob⁃lem[C]//2007 IEEE International Conference on Grey Systems and Intelligent Services.November 18-20，2007，Nanjing，China.IEEE，2007：1587-1592.

[6] LI X Y，GAO L.An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem[J].International Journal of Production Economics，2016，174：93-110.

[7] XING L N，CHEN Y W，WANG P，et al.A knowledge-based ant colony optimization for flexible job shop scheduling problems[J].Applied Soft Computing，2010，10（3）：888-896.

[8] ZHANG G H，SHAO X Y，LI P G，et al.An effective hybrid par⁃ticle swarm optimization algorithm for multi-objective flexible job-shop scheduling problem[J].Computers & Industrial Engi⁃neering，2009，56（4）：1309-1318.

[9] 姚远远，叶春明.求解作业车间调度问题的改进混合灰狼优化算法[J].计算机应用研究，2018，35（5）：1310-1314.

[10] ZHANG G H，GAO L，SHI Y.An effective genetic algorithm for the flexible job-shop scheduling problem[J].Expert Systems with Applications，2011，38（4）：3563-3573.

[11] 王佳怡，潘瑞林，秦飞.改进遗传算法求解柔性作业车间调度问题[J].制造业自动化，2022，44（12）：91-94，106.

[12] KACEM I，HAMMADI S，BORNE P.Approach by localization and multiobjective evolutionary optimization for flexible jobshop scheduling problems[J].IEEE Transactions on Systems，Man，and Cybernetics，Part C （Applications and Reviews），2002，32（1）：1-13.

[13] BRANDIMARTE P.Routing and scheduling in a flexible job shop by tabu search[J].Annals of Operations Research，1993，41（3）：157-183.

[14] CHEN R H，YANG B，LI S，et al.A self-learning genetic algo⁃rithm based on reinforcement learning for flexible job-shop scheduling problem[J]. Computers & Industrial Engineering，2020，149：106778.

[15] NOURI H E，BELKAHLA DRISS O，GHÉDIRA K.Solving the flexible job shop problem by hybrid metaheuristics-based multiagent model[J].Journal of Industrial Engineering Interna⁃tional，2018，14（1）：1-14.

[16] JIANG T H，ZHANG C.Application of grey wolf optimization for solving combinatorial problems：job shop and flexible job shop scheduling cases[J].IEEE Access，2018，6：26231-26240.

【通联编辑：梁书】

基金项目“：基于进化算法求解柔性作业车间调度问题的研究”（ 编号：KJYB2024011）