赋予数学游戏教学新生命

本文结合“八面埋伏”一课的教学，阐述在设计时如何借助切块原理合理改造现有游戏，使其更符合小学生的认知特点，更有利于小学生学习。

第一次“切块”：情境创设时，将学生带入角色

切块原理源于心理学家乔治·米勒在1956年提出的“魔术数字7±2”理论。该理论认为人类短时记忆的容量限制大约在7个（±2）信息单元。通过将信息进行有效切块，可以扩大信息处理的广度和深度，从而提升记忆和理解能力。根据这一原理，教学中教师应有效地组织和呈现教学内容，以适应学生的认知特点。“引入”是教学的重要环节，好的教学引入能激发学生的学习兴趣，快速将其带入学习情境，因此成为“切块”的第一个节点。

教学片段：

秦朝末年，楚汉争霸天下。战争持续了多年，楚霸王项羽的领地已经越来越少，汉王刘邦乘胜追击，派韩信挂帅，率七十万大军追剿项羽。韩信设下了八面埋伏之计。

师：此时的你将化身为韩信，我们一起来包围楚军。

第二次“切块”：探索奥秘时，降低学生认知负荷

《庖丁解牛》是庄子哲学中的一则著名寓言，庖丁在解牛时，不是盲目地用力，而是顺应牛的自然结构，找到牛体的空隙，这样既省力又高效。善用切块原理的人如同庖丁解牛一样，能顺应学生认知特点进行教学设计，让学生学在最近发展区。以本环节为例，在引导学生探索奥秘时，有两个难点：一是低年级学生学习概念存在一定的困难；二是扫雷的本质就是逻辑推理，对于低年级学生而言，游戏规则相对枯燥及繁杂，不容易理解及掌握。为解决问题，需要教师采取适当的教学策略和方法来支持学生的学习。

1.将概念学习的过程切割为三个游戏。

“包围”是本节课的核心概念，为帮助学生用数学的思维理解这个概念，本环节设计了三个简单游戏，引导学生在玩中学，在层层递进的游戏中发现“包围”中蕴含的数学规律，并借助数学语言“共边”“共点”描述规律，发展学生的语言表达能力，为后续的学习打下坚实的基础。

教学片段：

师：请看，楚汉的排兵布阵图。

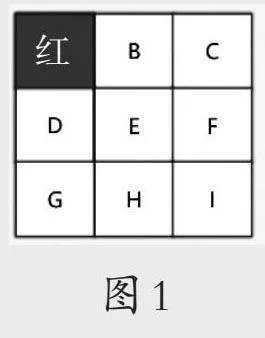
出示课件（如图1）。

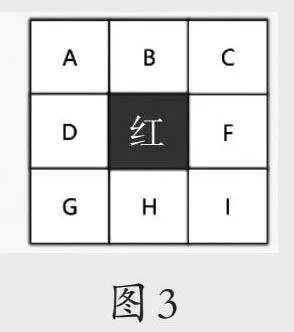
提出问题：红格代表楚军的位置，汉军用最少兵力包围了楚军，想一想，汉军占领的是哪些格子？

师生共同探讨，明确：汉军占领B、D、E就能用最少的兵力包围楚军。

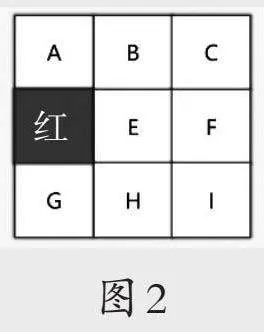
变换楚军的位置（如图2、图3），继续追问：楚军的位置发生了变化，那么汉军占领的又是哪些格子呢？

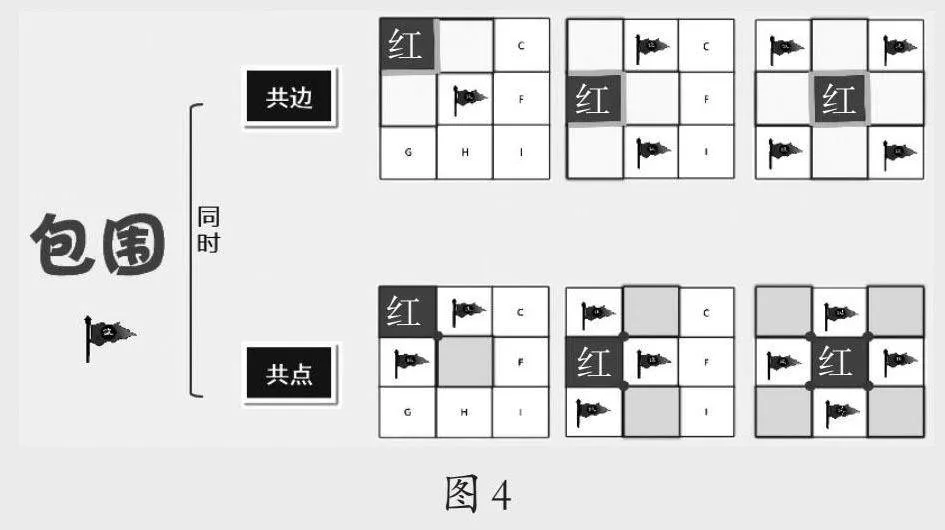
师：对比三幅排兵布阵图，想一想，包围红格的白格有什么特点？

引导学生对比总结：包围红格的白格要么与红格有“共边”，要么与红格有“共点”，如图4所示。

2.将规则理解的过程切割为三个游戏。

为更好地理解游戏规则，设计时将其切割成三个模块，层层递进，帮助学生理解和掌握。模块一研究理解数字与炸弹之间的关系，这是游戏的基础；模块二学习如何根据炸弹的数量填写对应的数字，这是方法的感悟；模块三要挑战如何根据数字确定炸弹的位置，这是经验的提炼。三个模块各有侧重，但都指向逻辑思维的培养，在观察、分析、比较中学会分析问题、辨识关键信息、提出合理的解决方案并进行有效的推理和判断。

教学片段：

（1）破解军事地图。

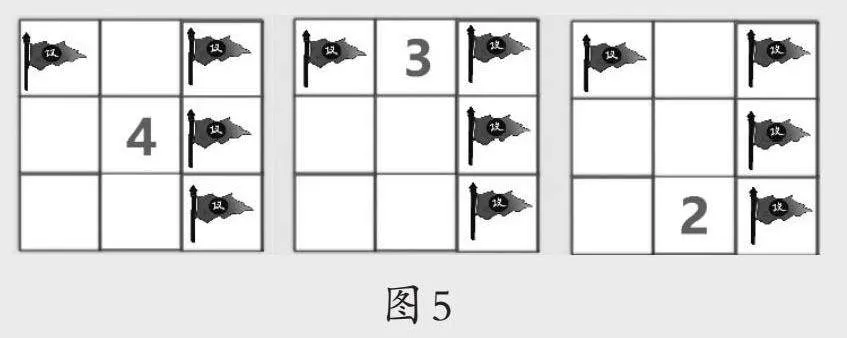
师：八面埋伏，让项羽压力越来越大，这时，他得到了三幅汉军的神秘军事地图（如图5）。

组织学生进行小组讨论：在汉军的三幅军事地图中，军队数量、所在位置都是一样的，但每幅图中标识的数字不一样，这些神秘的数字表示什么意思？

组织学生进行全班汇报，得出结论：神秘数字代表的是包围它的所有格子中埋伏军队的格子数量。

（2）绘制军事地图。

出示图6，提出问题：你觉得问号处该写几？

小结闯关秘籍：先找出包围它的所有格子，即确定包围圈，再数包围圈中军队的数量。

个人挑战赛：在图7所有白色空格处填入合适的数字。

（3）升级军事地图。

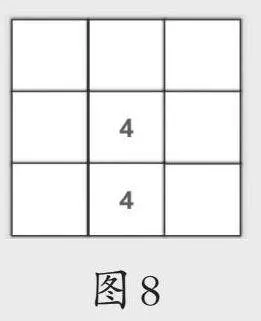
师：知悉军事地图被破解，汉军很恼火，连夜组织军事专家对地图进行了升级（如图8），你能根据数字找出所有军队埋伏的位置吗？

学生先独立思考，尝试破解，再和小组同学讨论，寻找闯关秘籍。

全班交流汇报：两个“4”的包围圈一样吗？想一想，从哪个“4”着手更好？为什么？

得出闯关秘籍：先观察分析每个数字所对应的包围圈，辨识关键信息，寻找突破口，然后，提出合理的解决方案。

第三次“切块”：运用知识时，增强学生自我效能感

“积小胜，为大胜”，在学生探究未知领域时，一次次成功的体验能增强学生的自信心，因此运用知识时，同样需要切块，合理设计进阶的学习任务。以本课为例，为培养学生寻找关键信息的能力，帮助学生理解关键信息对于解决问题和做出决策的重要性，设计了两个闯关练习，第一关重在感受特殊数字的作用，第二关重在感受特殊位置的作用，引导学生学会从不同的角度分析问题和信息，以得到更全面的理解，培养学生灵活思考和综合各种信息的能力。

教学片段：

师：孩子们，通过你们的不懈努力，升级版的军事地图也被你们破解了，真了不起，还要挑战吗？实战演练开始！

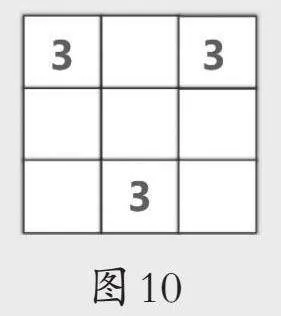
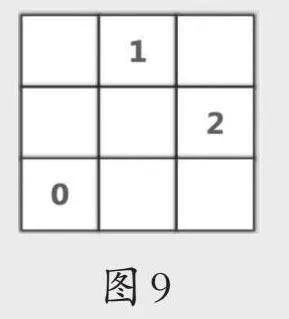
出示图9、图10，要求限时独立完成。提示：想一想，从哪个数开始推理比较好？

通过交流明确：“0”是一个非常重要的关键信息，根据它可以确定包围圈中没有埋伏军队的格子；数的大小并不直接决定信息的重要性或有用性，要灵活应用已有信息进行综合分析、多元思考，辨识出关键信息以进行推理，得出合理的解决方案。

课后反思

切块原理作为一种重要的信息处理策略，被广泛应用于教育实践中。切块后学生只需集中精力处理一个小块的内容，降低认知负荷，更易于掌握知识。特别是在小学阶段，学生正处于认知发展的关键时期，合理运用切块原理不仅可以有效提高学生的信息处理能力和学习效率，使学生更轻松理解和掌握数学知识，还能为学生在未来面对更复杂的现实生活问题时，提供有效的解决思路和方法。

但是，在使用切块原理时，要注意以下两点：一是要重视知识体系构建，避免知识碎片化。切块后，复杂的知识或问题被分解成更小、更简单的部分，有利于学生消化和理解，但也会带来认知的碎片化。教学中要引导学生“关联地学”，通过逐步展示和连接不同部分，让学生清晰看到知识体系的结构和内在联系，理解知识点之间的逻辑关系，逐步提高学生对知识的整体把握和深度理解。二是要提升问题解决能力，构建系统性思维。“切块”不仅仅是一种教的方法，更应该成为学的路径，面对复杂知识和问题，学生常常无从下手，学会将其分解成一个个可以完成的小任务，就可以逐步解决每个部分，这种分阶段解决问题的方法有助于培养学生的逻辑思维、分析能力。也就是说，在教学中，教师要注重学法指导，帮助学生养成“切块”的思维习惯，提升问题解决能力，构建系统思维。

（作者单位：广东深圳市福田区东海实验小学） L