定向、感知、分类、刻画:面积概念建构的四进阶

摘 要:“面积”是人教版《义务教育教科书数学三年级下册》第5单元的内容,也是首次出现面积的概念.较旧版教材而言,新版教材不再出示“物体表面或封闭图形的大小,叫作面积”这样明确的定义,而是突出学生对“面”的本质的充分感知.本文详述了“面是什么—面在哪里—面有不同—面可比较”四步进阶设计,通过突出学生对于“面”的感受和体验,帮助学生建构面积概念.
关键词:定向;感知;分类;刻画;面积概念
在图形与几何领域,从长度到面积,从一维走向二维,对学生来说是图形认识发展上的一次飞跃[1],具体而言,无论是从意义的角度还是从度量的角度,两者均存在本质的区别.通过分析学生“认识面积”的前测发现,三年级学生在面对一个封闭图形时,有57%的学生下意识关注到封闭图形的周长.学生在理解面积概念上有困难,特别是对“面”的感受很淡薄,不够深刻.为了有效帮助学生更好地感知和体验“面”,建构面积概念,教师可以尝试以下的教学设计.
1 面是什么:经历面与生活的联系,定向数学学习的面
教师出示“面”字.
师:看到这个字你想到了什么?
生:面积、面条、面包、面粉、面相……
师:同学们想到了各种各样与“面”相关的内容,那数学学习中的“面”到底指的是什么呢?本节课就一起来研究像数学书封面、桌面、黑板面这样的“面”.
【设计意图】教师从“面”字引入教学,联系生活,增加学生学习的趣味性,从而唤醒学生已有的经验.同时,教师根据学生的回答,帮助学生厘清哪些是数学中要学习的面,使学生初步了解数学学习的面是什么.
2 面在哪里:经历多感官的体验,感知数学学习的面
2.1 看一看,摸一摸,感知面多成片
教师展示被统一颜色覆盖的面,如黑板的面、树叶的面、数学书的封面和桌面,让学生对面有初步的感知.
接着,教师提出问题“你能像老师这样找一找周围物体上的面吗”.
生:音响上面有音响外壳的面、教室地板的面、教室前面的墙面、凳子上的面……
教师进一步引导学生摸一摸凳子上的面,让学生通过视觉和触觉来感知数学学习的“面”,鼓励学生用自己的语言来表达“面”.
师:在学习线的时候,我们都说它是一条条的,那么你能形容一下面吗?
生:面是一片片的、一块块的.
师:面是一片片的,像黑板这样一整片的大小就是面.
【设计意图】教师从黑板、树叶、数学书、桌子等具体的实物中抽象出面,让学生形象地感受到面,接着让学生列举在生活中看到的面,通过看一看、摸一摸去感受“面”,增加学生对“面”的具象了解.
2.2 辨一辨,理一理,感知面在体上
师:找到那么多的面,这些面都是单独存在的吗?它们都在哪里?
生:凳面在凳子上,地面在地上;面在某个物品的附近;面指的是某个物品上面的一个平面;面都是依附在某个物体上的.
学生的回答从具象的描述到特征的概括,语言越来越精练,感知越来越鲜明.
师:我们看得见摸得着的面都在物体上,简单来说就是“面在体上”.
2.3 探一探,悟一悟,感知面有边界
教师指着数学书封面之外的地方,再次提问“这里还是数学书的封面吗”,引发学生思考和讨论.
生1:我觉得不是,因为它不在物体的上面,而是在物体的外面.
生2:因为你手指的这一块面不是贴着这个物体的,所以我认为它不属于数学书的封面.
生3:我补充,面是有规定的,有范围的.
教师又指着数学书的外围一周继续追问“这是数学书的封面吗”.
生:外面一圈是一条线,面积是一整片的.你刚才指的应该是数学书封面上的周长.
【设计意图】教师围绕着“让学生深刻感知数学学习中的面,关注面的要素”,设计“面在哪里”的一系列探究问题,首先让学生充分感知面是一整片的二维图形,其次让学生发现面都是依附在物体上的,不可能孤立存在,最后让学生深刻认识面是有范围有边界的.这样的认知过程是深刻的,这样的本质体验是潜移默化的,不是直接告知的.
3 面有不同:经历比较活动,分类数学学习的面
首先,教师让学生找出指定学具材料中的面,分类感受面的不同.提供的材料有:薯片桶、树叶、纽扣、正方形和长方形卡片、纸巾盒、数学书、课桌、撕坏了的纸等.
接着,学生四人小组开展合作,通过看一看、摸一摸,找到这些物体上的面,比较这些面的异同.活动时间三分钟.
再次,学生分小组进行汇报.
学生总结:①这些图形的周长都不一样;②这些图形的面积不一样;③面的大小不一样;④图形面的弯度不一样,长方形卡片是平的,薯片筒的侧面是弯的;⑤这些面的形状不一样,撕坏了的纸面是一个多边形,而纸巾盒的上面就是一个长方形;⑥物体的材质不一样,表面的光滑程度不一样,叶子的面比较粗糙,而薯片筒侧面比较光滑;⑦这些物体的面积大小不同,而且有些面是不规则的,有些面是规则的.
最后,教师小结:观察的角度不同,小组之间的发现也不同,都各有各的价值,说明“面有不同”.
【设计意图】教师通过小组合作,让学生经历将不同的面进行分类的过程.从外观上看,面包括各种形状,有规则形状的面,有不规则形状的面;从形态上看,有些面是平的,有些面是弯曲的;从范围上看,面有大、有小,而且面的大小是确定的,是可描述的,是可度量的.这个环节的目的有两个:一是通过比较每个面之间的不同,从外观、形态和大小三个维度全面、深刻地理解“面”;二是强调了面的大小是确定的、可度量的,从而更好地过渡到下一环节.
4 面可比较:经历比较辨析,刻画数学学习的面
4.1 教师提供素材,让学生找出物体上的面并比较出九个面的大小
教师出示图1,让学生比较图中九个面的大小.
学生的汇报出现两种比较结果.一个小组认为,面的大小顺序是⑧>⑦>⑥>⑨>⑤>④>②>①>③;另一个小组则认为是⑧>⑦>⑥>⑨>④>⑤>②>①>③.
(2)教师梳理比较的方法.明显可观察分辨出的是⑧>⑦>⑥和②>①>③.⑥和⑨两个面可以用重叠的方法进行比较,发现⑥>⑨.所以,基本能确定的顺序是⑧>⑦>⑥>⑨>( )>( )>②>①>③.小组之间意见有分歧的是⑤和④的面,不能确定哪个比较大.
【设计意图】学生通过小组合作,将这些物品的面的大小按照一定的顺序进行排列,进而感受面的大小是可以比较的.同时,教师通过学生汇报,总结面的大小比较的方法是多元的,有些面直接观察就能看出大小,有些面可以用覆盖重叠的办法来比较,有些面则可以利用其他物品作为参照来比较.在这个活动中,特意放置了⑤和④两个面积相同而形状不同的面,一个是长方形,一个是正方形,学生得到不同的结论,难以精确比较这两个面的大小,这为后面统一度量单位的活动环节做铺垫.
4.2 学生借助测量工具,比较出有争议的两个面的大小
教师提供大正方形、小正方形、圆形、三角形、正方形卡片和长方形卡片等学具,引导学生借助学具合作完成正方形卡片和长方形卡片大小比较.
(1)学生反馈各自的探索结果:用4个大正方形就可以填满长方形卡片和正方形卡片,说明它们一样大;用圆片去摆,都用了16个圆片,说明它们一样大,但16个圆片不能等同于长方形或正方形卡片的面积;用小长方形的标准去摆,发现长方形卡片上用了25个,而正方形卡片上用了24个之后还有缺口,不能铺满.
(2)教师追问:那能不能比出长方形卡片和正方形卡片这两个面的大小.
生1:再拿一个小长方形剪成两半,正好就可以补上缺口,那么两张卡片都是25个长方形那么大,可以说明两张卡片面积一样大,就是操作麻烦了点儿.
生2:尝试用了三角形,但无论怎么摆,就是不能全部铺满.
生3:选择小正方形去铺,铺了一部分,可是发现要用的太多,太麻烦就放弃了.
(3)教师把准备好的两份用大正方形和小正方形标准铺成的卡片分别展示,让学生观察,看看有何发现.
学生得出结论:要比较出大小,用同样大小的工具去铺,正方形能将这两张卡片的面都铺满,用小的麻烦,用大的方便,所以建议大家用大的正方形做标准,可以准确又方便地数出个数.
【设计意图】此环节主要解决“如何比较两个面积相等但形状不同的面的大小”问题.学生利用教师提供的各种各样的度量标准,通过动手操作发现圆和长方形可以度量这两个面,但是用圆来度量还不够精准,用正方形度量能够精确且快速地表征出长方形和正方形的面积.同时,学生通过比较用大正方形和小正方形来表示测量的结果,得出结论:①用圆、三角形可以度量,但不够精准;②用大正方形、小正方形可以精确度量,但不好比较;③为了比较,所以要统一度量单位.
4.3 学生经历累加过程,数出图形面积,刻画出图形大小
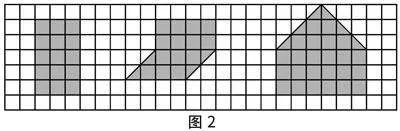
教师出示方格图(如图2),让学生尝试以小正方形为标准,数出方格纸上三个图形的面积.
学生交流数个数的方法,分别描述出图形的大小:第一个图形有15个小正方形.第二个图形可ipHbO9a5irtf0CvB70JhzA==以把那个斜的三角形移到右边,拼成一个完整的正方形,共16个小正方形.第三个图形也可以把上面的三角形拼成正方形,这样就有27个小正方形.
教师总结:今天这节课我们通过看一看、找一找、摸一摸,认识了面,明白了“面是什么,面在哪里”;通过辨一辨、测一测、比一比,了解了面,知道了“面有不同,面可比较”;用统一的标准对面进行测量,从而比较出图形的大小.
【设计意图】一个图形的大小,即这个图形的面积,是这个图形本身的一种数学属性,也是它本身所拥有的一种数学特征.[2]这个图形的大小可以度量,即用一个单位作为标准去度量,并用度量的结果来描述面的大小.
要精确地刻画一个图形,就需要刻画它的大小,或者刻画它的性质.在本课的教学中,要紧紧抓住刻画图形的大小这个重点.教师可以尝试让学生用自己的标准,用自己的方式去描述图形的大小.通过描述,学生可以感受到,因为度量单位不同,所描述出来的面积也不同.[3]由此,学生深刻体会统一度量标准的必要性.
参考文献
[1] 李兰瑛.在操作体验中理解概念——“什么是面积”教学实践与反思[J].教学月刊小学版(数学),2018(6):15-18.
[2]顾晓东.把握本质,精致概念建构过程——以“认识面积”教学为例[J].教学与管理,2014(26):44-46.
[3]唐慧荣,章勤琼.基于学习路径分析的“面积”单元整体教学——促进单元核心概念理解的课例设计[J].小学教学(数学版),2021(4):12-15.

