中小学数学“问题提出”的研究：回顾与展望

摘 要：从CSSCI（含扩展版）数据库、人大复印报刊资料全文数据库和SSCI数据库中选取2000—2022年间发表的有关数学问题提出的173篇文献。借助SATI、VOSviewer等软件对所选文献的来源、年份、机构及地区、核心作者、关键词等信息进行统计分析；运用内容分析法，对所选文献的研究方法、研究对象和研究主题进行梳理统计和深入分析。由此发现，国内外数学问题提出研究表现出三大取向：研究方法以实证研究为主的科学性取向，研究对象以小学生和职前教师为主的阶段性取向，研究主题以教学和教师教育为主的实践性取向。从而为后续研究提供坚实的基础，作出方向的指引。

关键词：数学教育；问题提出；研究综述；文献分析

*本文系全国教育科学“十三五”规划课题“面向核心素养的数学问题情境教学测评模型研究”（编号：XHA180286）的阶段性研究成果。夏小刚为本文通讯作者。

问题提出（Problem posing）是基于特定的问题情境形成并表达问题的认知活动，同时兼具教学手段和教学目标的角色［1］。数学问题提出一直是国内外数学教育界感兴趣的话题之一，许多研究者都给予了广泛关注，但直到近二十多年，才成为一个尤为活跃的研究领域［2］。为明晰这一领域的研究现状，尚亚明、陈汉君等对国内数学问题提出的研究、国内外数学问题提出的过程性研究、国外数学问题提出能力的影响因素研究等文献进行了梳理和分析［3-6］。但研究内容有一定的局限性，缺乏对国外数学问题提出研究成果的整体介绍。基于此，本文试图对国内外数学问题提出的高水平文章进行系统全面的分析，从中审视数学问题提出的研究现状，窥探数学问题提出的研究趋势。

一、 文献选取与分析方法

（一） 文献选取

为了保证所选文献的专业性和代表性，我们选取了三个数据库。其中，中文数据库是CSSCI（中文社会科学引文索引）（含扩展版）数据库和人大复印报刊资料全文数据库，英文数据库则是SSCI（社会科学引文索引）数据库。在三个数据库中，将索引年限设定为2000—2022，关键词设置为“数学”“问题提出”“提出问题” “Mathematical”“Problem Posing”等，并进行多重多次检索。在CSSCI（含扩展版）数据库中共检索到79篇文献；在人大复印报刊资料全文数据库中共检索到58篇转载文献，去除与前述重复的文献后，共得到有效文献28篇；在SSCI数据库中共检索到83篇文献，去除更正、修订和回应等文章后，共得到有效文献66篇。因此，最终从三大数据库中得到有效文献173篇，其中中文文献107篇，英文文献66篇。

（二） 分析方法

借助SATI、VOSviewer等软件，对所选文献的来源、年份、机构及地区、核心作者、关键词等信息进行统计分析，并绘制文献作者和关键词的共现图谱；运用内容分析法，对所选文献的研究方法、研究对象和研究主题进行梳理统计和深入分析。由此，回顾国内外数学问题提出的研究脉络与热点，展望未来的研究方向与重点。

二、 中小学数学“问题提出”文献的相关信息分析

（一） 来源分布

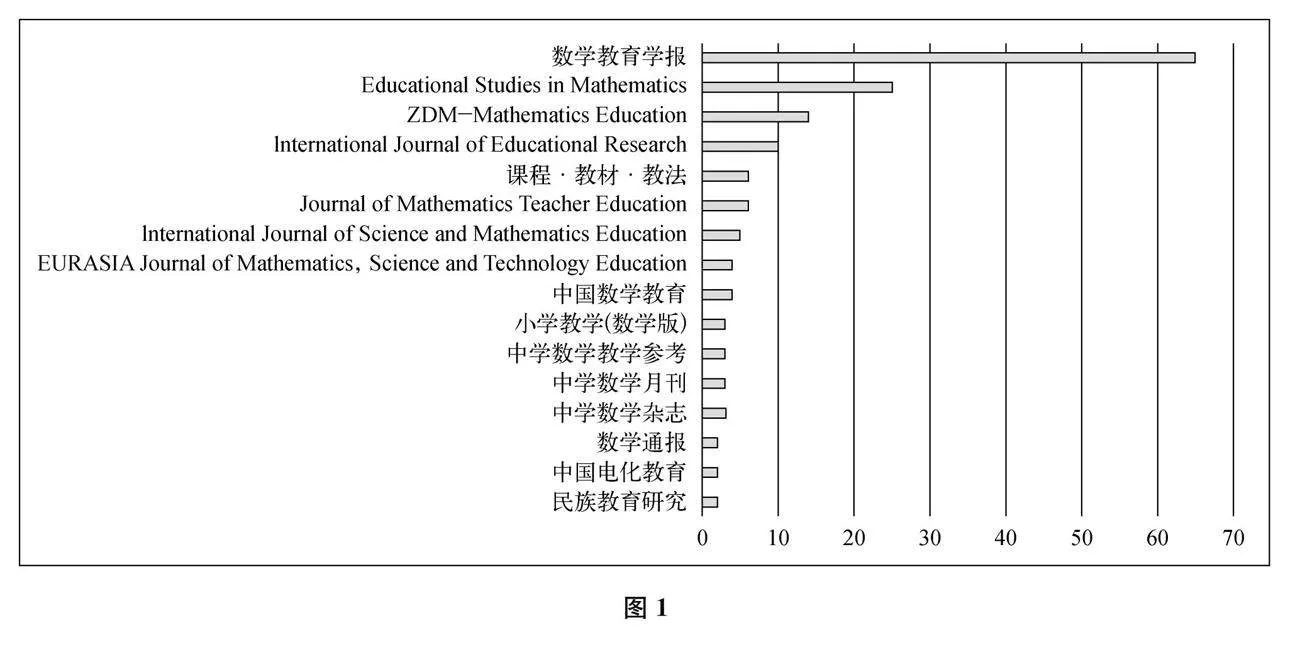
173篇文献共来源于32本不同的期刊。其中，中文期刊24本（CSSCI期刊8本，人大复印报刊资料转载来源刊16本），SSCI期刊8本。对发文量在2篇及以上的期刊进行统计，得到图1（其中，《中国数学教育》《小学教学（数学版）》《中学数学教学参考》《中学数学月刊》《中学数学杂志》《数学通报》等刊物系人大复印报刊资料转载来源刊）。《数学教育学报》刊登的数学问题提出的研究论文多达65篇，其中20篇被人大复印报刊资料全文转载，占该领域被全文转载的文章数的40.8%。可见，无论是数学教育领域还是教育综合领域，国内外近年来都对数学问题提出研究领域给予了很大的关注；《数学教育学报》在数学问题提出研究领域贡献了核心力量。

（二） 年份分布

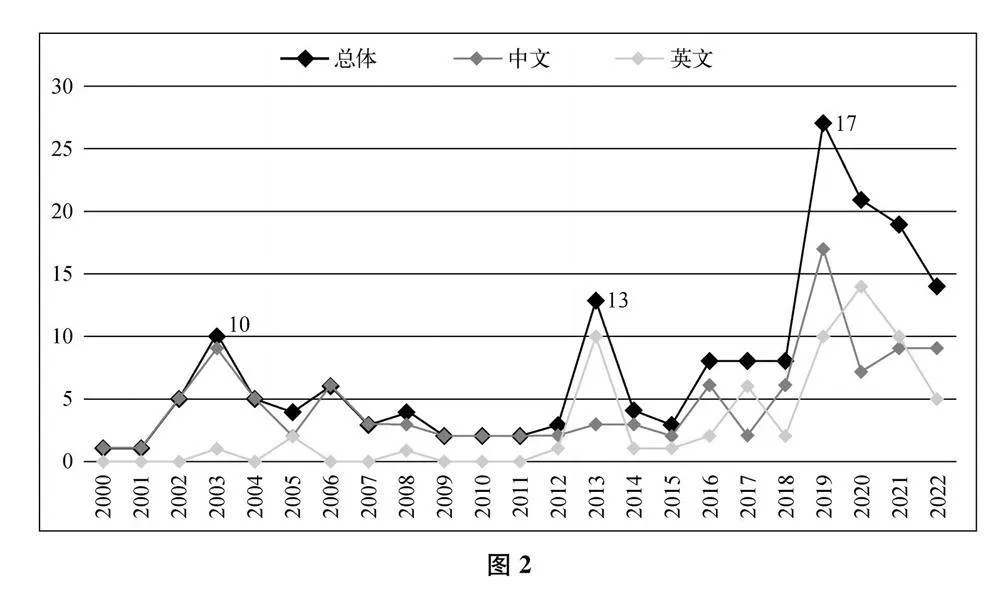
对173篇文献发表的年度进行统计，得到图2，发现该领域经历过三个研究热点阶段。第一个热点阶段集中在2003年，主要表现为吕传汉、汪秉彝等带领贵州师范大学数学教育团队在西南地区以及国内20余个省市开展“情境—问题”课堂教学改革实验研究，其核心是将“质疑提问”、培养学生的问题意识、提高学生提出问题和解决问题的能力贯穿于教学过程的始终［7］。第二个热点阶段集中在2013年，主要由Educational Studies in Mathematics杂志于2013年推出特刊，其想法诞生于2009年PME33跨国工作组进行题为“数学学习中的问题提出：建立研究的理论基础”的研究，涉及问题提出的本质、学生的数学内容知识与数学问题提出能力之间的关系、问题提出的情境对教学过程的影响、问题提出研究的发展方向等内容［8］。第三个热点阶段集中在2019—2021年，首先，Inter-national Journal of Educational Research杂志在2019年重点讨论了基于问题提出的教师专业学习和教学活动方面的问题；其次，蔡金法、Roza Leikin

在Educational Studies in Mathematics杂志上发出数学问题提出中情感问题的论文征求［9］后，该杂志在2020年集中探讨数学问题提出中各阶段学生在认知、情感、信念等心理层面的差异与影响，丰富了数学教学和学习中问题提出与情感联系的研究；最后，西南大学数学教育团队在蔡金法教授的带领下进行了数学问题提出对教师专业发展和学生创新能力提升的长期跟踪研究，提出了“问题提出”主题式培训促进小学数学教师专业发展的理论基础和教师专业发展的一般路径［10-11］，并且在重庆小学数学“问题提出”教学工作坊中进行了实证研究，获得了丰硕的研究成果。国内外研究者的兴趣和努力将数学问题提出领域的研究推向高潮，高质量的研究成果正不断出现。

（三） 机构及地区分布

173篇文献的第一单位主要有四种类型：高等院校（80.9%）、中小学（11.6%）、科研机构（4.0%）、教研部门（3.5%）。其中，高等院校是该领域研究的主力军，并且，国内以师范院校为代表，国外以综合性研究型大学为主。对这些机构所属的国家和地区进行统计，中文文献共涉及19个省市，排名前5的地区依次是：贵州（19.6%）、重庆（15.9%）、北京（11.2%）、浙江（9.3%）、上海（7.5%）；英文文献共涉及18个国家，排名前5的国家依次是：美国（33.3%）、中国（19.7%）、以色列（9.1%）、土耳其（6.1%）、罗马尼亚（6.1%）。可见，国内自20世纪90年代开启针对学生问题提出能力培养的专门研究，完成了从理论构建到实践检验的整个研究过程，随后又将研究视角指向问题提出的各个方向；国际上中美两国对这一领域最为关注，美国自20世纪80年代开展以“问题解决”为核心的数学教育改革运动到开启“问题提出”的数学教学研究，已经逐步将“问题提出”从“问题解决”中脱离出来，使之成为一个独立的研究领域。

对发文量在2篇及以上的第一单位进行统计，得到表1（其中，名称中既有中文也有英文的，表明该单位不仅发表了中文文章，也发表了英文文章，其发文量则是中文文章和英文文章数量的总和）。从中可以发现，国内发文机构集中在西南地区和华东地区，西南地区发文量最多，以西南大学和贵州师范大学为代表（由这两所大学分别主持的小学数学教师“问题提出”教学的相关研究和数学“情境—问题”教学模式的实验研究在国内数学教育界具有重要影响）；国外发文机构以特拉华大学为代表，伊利诺伊州立大学、密歇根州立大学等美国著名大学的研究者也表现出对这一领域的研究兴趣。

（四） 核心作者分布

核心作者是各学科研究领域造诣较高、学术活动较频繁、发表论文数量较多且影响较大的作者［12］。他们是学科研究的坚实基础，通过了解他们的研究成果，可以窥探某一领域研究的发展过程和前沿方向［13］。核心作者候选人的最低标准一般利用普赖斯公式（M=0.749Nmax）计算［14］，我们采用被引用量和发文量相结合的方式来筛选核心作者候选人。

首先，确定最低被引用量。173篇文献中被引用量最高的中英文论文的第一作者分别是夏小刚和Sandra Crespo，论文被引用的次数分别是390和124。利用普赖斯公式计算（0.749×390=14.79，0.749×124=8.34），得到中文文献被引用量达到15次及以上或英文文献被引用量达到8次及以上的作者可以入选核心作者候选人。

其次，确定最低发文量。173篇文献中发文量最多的中英文作者都是蔡金法（Jinfa Cai），其中文发文数量为25篇，英文发文数量为18篇，总计43篇。利用普赖斯公式计算（0.749×43=4.91，0.749×25=3.745，0.749×18=3.18），得到中英文综合发文量达到5篇及以上、中文发文量达到4篇及以上或英文发文量达到3篇及以上的作者可以入选核心作者候选人。

由此，确定核心作者。符合条件的核心作者候选人共计185位（中国学者108位，外国学者77位）。筛选同时符合两个条件的文献作者，经过去重统计，得到核心作者18位（中国学者9位，外国学者9位），他们共发文64篇，占173篇文献数量的37.0%；所发论文共被引用4660次，占173篇文献总被引用量的67.4%。这18位核心作者的相关情况如表2所示（有3位核心作者没有以第一作者的身份发表过相关论文，因此不在表格中；“发文次数”和“篇均被引次数”中的“1”和“n”分别表示以第一作者的身份和以第n作者的身份；“被引次数”截止到2023年8月；表格按照以第n作者身份的发文次数，即发文总次数排序）。

基于上述统计，可以发现：中美两国的研究者正合力拓展和加深这一领域的研究。观察核心作者一作的单篇最高被引文献，可以大致把握这一领域从“情境—问题”的教学和学习、学生数学问题提出能力及其与认知、情感的关系到基于问题提出的数学教师专业发展的研究脉络。

利用VOSviewer软件分别绘制中文作者共现图谱和英文作者共现图谱，得到下页图3和图4。

从发文数量、发文质量、作者合作关系网等多个方面考察，可以发现，蔡金法教授是国内外“数学问题提出”领域研究的领军人物。近年来，蔡教授与西南大学的研究者进行多次合作交流，将国内外的研究力量聚集起来，形成了较为稳定的作者群。

（五） 关键词分布

文献关键词是对研究内容的主题提炼和表达。通过对关键词出现频次的统计，可以直观地了解该领域的研究热点，同时为后续研究主题的划分贡献参考价值。合并同一含义的关键词（如“问题提出”和“提出问题”）后，出现频次前十名的关键词依次是：问题提出（problem posing）、问题解决（problem solving）、数学情境（mathematical situation）、数学问题（mathematical problem）、数学教学

（mathematical teaching）、问题提出能力、教师学习（teacher learning）、teaching mathematics through problem posing、小学数学、数学课程（mathematical curriculum）。由此可知，研究主要聚焦在问题提出与问题解决、问题提出与数学情境、教学与教师教育、问题提出能力和数学课程等方面。除此之外，创造力、情感、评估和教材等方面研究也较多。

运用VOSviwer软件绘制关键词共现图谱，并按文献发表年份进行可视化呈现，得到图5。可见，2005年之前，研究主要聚焦在数学情境、教学实验、创新教育方面；2005—2010年，研究主要聚焦在问题解决、数学应用、职前教师和教学思考方面；2010—2015年，研究主要聚焦在创造力、情感、问题提出能力及其培养策略、数学课程、比较研究方面；2015至今，研究主要聚焦在小学数学、教学改革、评价、教师专业发展、教师学习、认知过程方面。此外，针对国内外数学问题提出教学研究现状的述评文献只有1篇，于2005年发表，夏小刚认为彼时国内的“数学问题提出”在过程性特征研究、评价研究、变量研究、教学和教师教育研究等方面有所欠缺［30］。而观察近年来对这一课题的研究内容，发现已逐渐覆盖上述方面。

三、 中小学数学“问题提出”文献的具体内容分析

（一） 研究方法分析

教育研究的方法可以分为实证和思辨两大类，实证方法又可分为量化、质性、调查、实验等具体类型。对173篇文献所使用的研究方法进行统计（如果使用了多种研究方法，按照最主要的研究方法进行统计），发现：实证研究为此领域的主流研究类型，共计130篇，占比75.1%（其中，量化研究有87篇，质性研究有43篇）；以问卷、测试卷等为主的调查研究是该领域最常使用的研究方法，达到58篇。相比之下，国内以思辨、调查、实验等传统研究方法为主，而国外的研究方法更加丰富，如：Lorna Headrick

等［31］使用经验抽样法捕捉高中学生在数学课堂中自发问题提出与情感参与的程度，这种方法能够获取最接近个体真实经验的数据［32］；Marie Tichá

等［33］对职前小学教师提出的问题和各种类型的书面反思等文本内容进行语义分析，经过不同阶段的分析找到各个问题的共同特征，以揭示他们对分数概念理解的缺陷。

（二） 研究对象分析

在教育研究中，实证研究的对象通常是学生、教师和文本等。对130篇实证研究文献的研究对象进行统计，结果显示：以学生为研究对象的有44篇，占比33.8%；以教师为研究对象的有40篇，占比30.8%；以文本为研究对象的有22篇，占比16.9%；以案例为研究对象的有18篇，占比13.8%。进一步分析发现，学生对象涉及范围较广，包含儿童、小学生、初中生、高中生、高职生和大学生，其中最多的是小学生，其次是高中生和初中生；教师对象则涉及职前教师、小学教师、初中教师和高中教师，其中将近一半的是职前教师。由此可知，学生和教师是“数学问题提出”实证研究的主要研究对象，并且小学生和职前教师是重点关注对象。这也反映出在数学学习起步阶段培养学生问题提出能力的重要性［34］，以及研究者对通过“问题提出”培养未来数学教师的教学能力，即教师专业发展研究的重视。此外，国外研究者更善于挖掘文本研究对象，如课程任务和作业、教学反思、学生日记等，国内研究者则聚焦在一些纲领性文件以及教材上，文本研究对象的类型较为单一。

（三） 研究主题分析

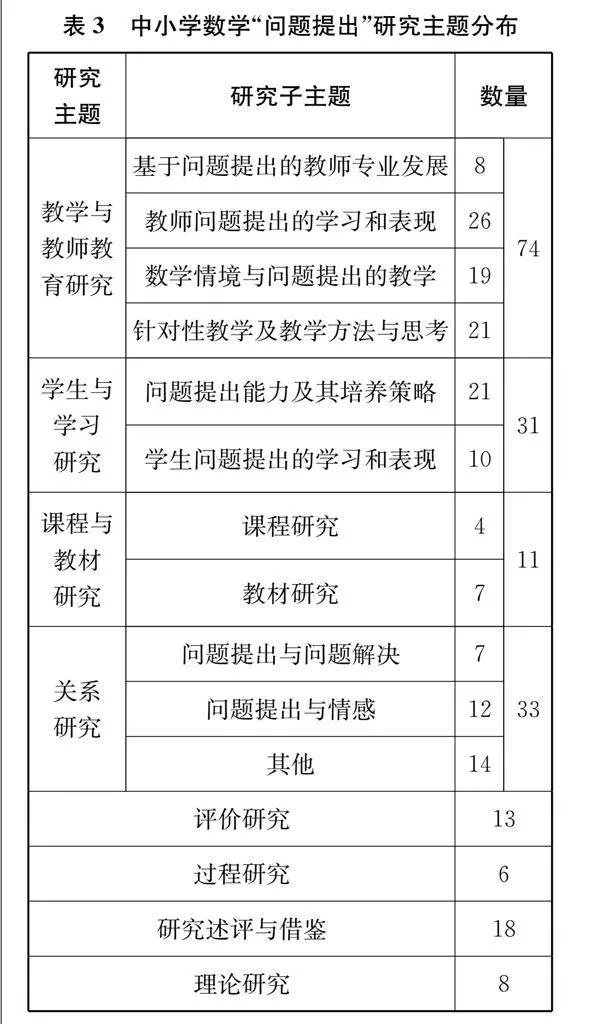
根据上述关键词分布，参考国内外学者对数学问题提出领域的主题划分［35-36］，提出“数学问题提出”领域的8个研究主题以及相应的子主题。由此，对173篇文献的研究主题进行统计（如果包含了多个研究主题，将各个主题分别记入），得到表3。

1. 教学与教师教育研究

教师专业发展是国内数学教育研究的五大核心主题之一［37］，在国外数学教育界也一直备受关注。蔡金法提出了主题式教师专业发展的模式，其基本假设［38］

是：教师通过学习（培训），获得教学知识的增长以及教学信念的改变，从而改进课堂上的教学行为，促进学生的数学学习，提高学生的学习能力和学业水平。基于这一理论假设，研究者开始帮助教师学习使用问题提出进行教学的实证研究。他们要求教师完成三项问题提出任务：（1） 在给定的情境、数学表达式或图表信息中，提出数学问题；（2） 在给定的情境、数学表达式或图表信息中，预测学生可能提出的数学问题；（3） 设计数学问题提出教学任务，要求学生在教师设定的情境中提出数学问题。研究结果显示，教师不仅具有提出多个复杂数学问题的强大能力，也具备将问题提出作为一种数学教学任务的信心。与此同时，研究者还专门针对教师的表现、教学信念和课堂行为进行了研究［39-41］，所得结果符合上述理论假设，进一步证明了通过“问题提出”主题式培训促进教师专业发展的可行性与必要性。目前，教师专业发展工作坊围绕小学数学“数与代数”领域开发了部分优秀教学设计案例［42-44］，但是其他知识领域的研究还较为欠缺。

教师问题提出的学习和表现研究主要发表在英文期刊上，重点关注职前教师对问题提出的认识和理解以及在问题提出过程中的学习与表现。作为问题提出的新手，职前教师缺乏问题提出的技巧和信心，更喜欢问题解决类任务，这将减少学生在数学课堂中提出问题的学习机会［45］。Nerida F.Ellerton认为要重视学习者主动提出问题的过程，他在从被动到主动的连续体概念上提出了一个主动学习框架（如图6所示），用于解释问题提出在数学课堂中的重要作用。Sandra Crespo

等［46］从一个独特的视角（如何帮助职前教师学会提出问题教学以达到教育公平的目标）研究发现，相互依赖、个人和群体的责任感、解决问题的多种能力这三种群体价值标准应该在引导教师进行问题提出的数学任务中作为重要衡量标准，而不是只关注教师的认知需求。

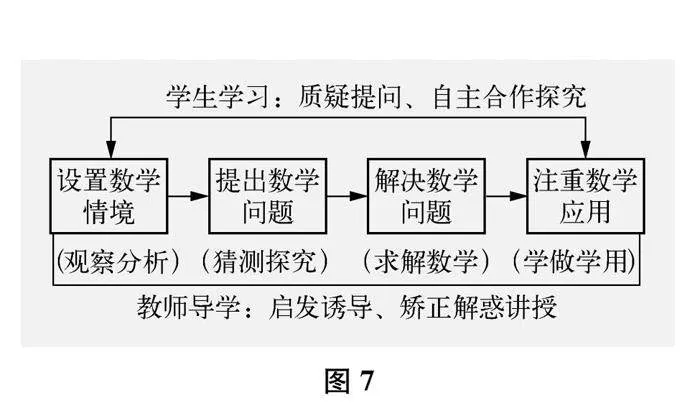
数学情境与问题提出的教学研究主要集中在21世纪初，是一个较为早期的研究方向。吕传汉和汪秉彝［47］通过反思性研究和中美“数学问题提出与解决”的跨文化研究，发现学生问题解决的能力较强，但问题提出的能力较弱，这严重制约了学生创新意识的发展，从而提出了“情境—问题”教学模式（如下页图7所示），该模式以提出数学问题为核心，力图实现数学创新教育的目标［48］。此外，该教学模式还具有提升数学学习兴趣、缓解数学学业焦虑的作用［49］。

第四个子主题主要是在具体的数学知识下或教学环节中探讨如何进行数学问题提出教学，并给出一些教学实践案例。比如：吴增生

等［50］以“等腰三角形”为例，基于单元整体教学设计，使用几何大观念引领学生进行问题提出与解决的教学策略，分别在城市和农村进行教学实验，结果显示，学生问题提出与解决的成绩提升明显，该教学策略可以有效促进学生提出并解决高质量的问题；桂潇爽

等［51］以“y=Asin（ωx+φ）”为例，从三种角度对同一内容进行问题提出教学——实际现象、模型构建和教材理解，并给出了相应的教学案例；徐彦辉［52］

将目光聚焦于波利亚解题思维的第四个过程“回顾与反思”，以“判定等腰三角形两腰上的中线相等”的一道课后习题为例，提出了在解题后经过证明、逆、特殊化、一般化、拓展、进一步拓展，即改编、引申和推广原有命题进而提出新问题的方法，又将新问题再次进行上述步骤，如此循环往复，提出更多的新问题。总体来看，教学实践案例覆盖的学段和知识内容都较为匮乏。

2. 学生与学习研究

学生与学习研究主题下的两个子主题相互关联，因而放在一起讨论。学生的问题提出能力是一个经久不衰的研究话题，研究者调查各类学生问题提出能力的现状，分析其特征、差异与主要影响因素，观察学生在问题提出活动中的表现，总结学生问题提出能力发展的特征，以给出相应的培养策略或教学建议。在现状调查中，得到的结果近乎一致，即学生的问题提出能力整体较弱，缺乏问题意识［53-55］，但是存在明显的地域差异，城市学生好于农村学生。除调查研究外，也有学者通过实验研究和课堂观察来探索培养学生问题提出能力的策略，根据学生的表现认为在开放情境下他们具有问题提出的潜能，提出设计开放情境、鼓励好奇好思好做、促进联想、开展问题接龙、进行问题分类和评价的小学教学实践策略［56］。还有学者比较关注问题提出能力的发展规律。如：李怀军和张维忠［57］

在韩琴和胡卫平［58］

研究的基础上，进一步明晰了小学生数学问题提出能力的发展趋势、关键期以及性别差异，并提出了相应的建议。此外，有学者将教育技术融入学生问题提出的活动中，发现在多媒体环境中让学生上机操作感受问题的生成过程，有利于激发学生的问题意识［59］。张屹

等［60］则在智慧教室环境下使用APT教学模型构建《两位数乘两位数练习题》教学设计，以此进行教学实验。结果显示，这一教学设计有利于对学生问题提出能力和问题解决能力的培养，但对问题解决能力的培养更为明显。

3. 课程与教材研究

问题提出在国内外数学课程标准中不断被提及，重视程度越来越高，但总体上还是重理论思考，缺乏实践性。对此，不同学者有不同的看法。王嵘等［61］

认为，教师要灵活调整教材中的问题，以获得更具价值的教学任务，并为学生进行问题提出活动提供机会；陈婷

等［62］指出，官方文件需对“问题提出”进行概念界定，并在教材、教学参考书等教学资源中呈现更多的问题提出教学案例，以及提升对问题提出目标表述的精准度，以此加强课程实施者对问题提出教学的理解和操作性；许天来等［63］

也认为，要在教材中增加问题提出活动，助力教师进行问题提出教学。随后，郭玉峰等［64］

guB6FgCZ9BkjPCQWD1rtF78tsrq25+4PI+sNtnuvHNw=

就“问题提出”融入中小学教材的现状和困境进行了深度剖析，并提供了三条解决思路。其他有关的教材研究则以横向比较研究为主，涉及两个方面：国际教材比较（如中美比较［65-66］

和中日比较［67］

）和国内不同版本教材比较［68-69］。以上研究根据各国、各版的不同特点，所涉及的比较维度也不尽相同。另外，有一篇教材纵向比较的文章，通过比较近70年里我国数学教材中“数与代数”领域问题提出任务的比例和分布，发现随年级的增加，问题提出任务的数量反而减少［70］。这一发现同样引人深思。

4. 关系研究

在诸多与问题提出有关的对象中，问题解决是联系最紧密的一个。国外学者很早就发现学生提出问题的表现与他们解决问题的表现有关［71］；国内学者也通过对小学生的测试，发现问题提出能力与问题解决能力存在密切关系［72］。一项最近的研究发现，学生若拥有正确解决问题的能力，则更有可能拥有提出问题的能力，且所提的问题是可解决的，特别是，他们对问题提出任务，会有更好的理解；然而，研究者认为，问题提出与问题解决之间的复杂关系和认知差异还需要借助脑电图等心理学研究方法进行深入探索［73］。

近年来，越来越多的研究者开始关注问题提出中的心理特征，如情感、认知、动机等，这也体现出研究开始触及学生心理活动的微观层面。Meng Guo

等［74］借助中国苗族学生寻找情感与问题提出存在关系的定量证据。他们基于期望值理论（EVT）测得：学生的自我概念和内在价值对问题提出有积极影响，而考试焦虑有消极影响。Lorna Headrick

等［75］参与的一项研究显示，对美国两个不同区域的高中生来说，出现自发问题提出现象的期间，学生对数学任务的负面情绪较少。上述两项研究分别展现了情感对问题提出和问题提出对情感的影响，并且二者都显示出积极面的正相关关系。也有中国学者通过为期一年的问题提出教学实验，发现实验组学生在数学学业成绩和数学情感方面的提高程度都显著高于控制组学生，并且学业水平较弱的学生提升更为明显［76］。此外，还有问题提出与数学活动经验、数学内容知识、元认知、自我效能感等方面的关系研究，即问题提出与学生数学学习过程中其他特征的关系研究愈发广泛。

5. 评价研究

早期的评价研究聚焦在学生的问题提出能力上。吕传汉教授团队就此发表了三篇论文，逐步形成了以问题的数量、种类和独创性为标准的学生问题提出能力评价体系［77］，该评价体系成为后来研究者借鉴的范本。Osman Cankoy

等［78］则从更多的角度建立了小学生问题提出能力的评分标准，并通过独立评估者使用或不使用该标准进行对比实验，发现使用此标准不仅提高了评分者之间的可靠性，还能更明显地揭示学生之间的差异，具有较高的参考价值。而后，研究者开始将问题提出作为评价其他水平或能力的标准，如将问题提出作为衡量课程对学生学习效果的指标［79］。Ali Bicer等［80］通过对照实验揭示了问题提出对学生数学创新能力的干预，认为问题提出活动能培养学生的数学创造力，其表现可以作为学生数学创造力（流畅性、灵活性、原创性等）的衡量标准，并开发了一个评分标准。宋乃庆等［81］

则从学生所提问题的“合理性”（包括“扩展性”和“内容性质”两方面）来考查学生问题提出的表现，以测试他们对某一数学概念的理解。除了对学生的评估，还有学者利用问题提出来评估教师的数学理解［82］、未来教师的几何证明技能和创造力［83］。可见，“问题提出”成为一种有效的评估手段是具备一定的可行性和发展空间的。

6. 过程研究

专门以问题提出过程为主题的研究较少，对问题提出“过程”也没有明晰的界定。在这些专门的研究中，Constantinos Christou等［84］

根据前人的研究提出了一个问题提出认知过程的理论驱动模型，并对该模型进行了评估。结果表明，学生提出问题涉及四个认知过程（理解、翻译、编辑和选择），其中编辑和选择过程对学生问题提出能力的影响更大。Lukas Baumanns等［85-86］

进行了两项基于结构化情境的问题提出过程研究，他们先开发了一个模型来描述和分析问题提出过程，基于结构化情境确定了五种过程性活动（情境分析、变化、生成、解决问题和评估），并通过了验证者之间的一致性验证；后基于结构化情境问题调查了职前教师问题提出过程中的元认知行为，即在计划、监控和控制以及评估中提出问题的元认知活动，总共确认八项行为活动，特别地，发现元认知行为可以初步评估问题提出过程的质量，为问题提出过程的评估提供了新视角。事实上，有关问题提出过程的研究并不算少，它常常蕴藏在其他的主题研究中。尚亚明［87］

把问题提出的过程研究分为三类来述评：学生提出问题时的心理认知过程，学生学习过程中的情感、态度及其变化过程，哲学视角下问题提出所经历的程序和步骤。

7. 研究述评与借鉴

该主题主要可以分为三类：第一类是从宏观上对数学问题提出的研究现状、发展趋势进行概括和总结；第二类是对数学问题提出的某一方面进行研究述评，比较多地集中在问题提出教学方面；第三类是通过分析美国数学问题提出的研究发展，为中国的相关研究提供借鉴。第一类研究中，比较有影响力的是，10年前学者们在PME35论坛上围绕以下问题进行的探讨：提出问题与解决问题如何相互作用？如何通过让学生在开放式问题情境中进行数学探索和问题提出来提高他们的学习？使用问题提出作为评估工具是否可行？［88］

显然，10年后一些研究已经回答了上述问题，但是，这些研究还缺乏一定的广度和深度，上述研究方向仍不过时。第二类研究中，李怀军等［89］

认为，国外的一些研究从问题提出与教学整合的视角明确了“数学问题提出教学法”的内涵与教育价值，厘清了问题提出与问题解决之间的关系以及师生角色与关系，确定了问题提出情境创设的基本原则等；陈婷等［90］

将研究视角放向国内，聚焦于“问题提出”的教师教学，发现虽然70%的文章提供了“问题提出”的教学案例，但是实际情况相反，教师进行“问题提出”的课堂教学仍存在困难，可利用的资源较少。第三类研究中，于文华从宏观与微观两个视角对美国数学问题提出的认知领域进行了评论［91］；他们还以美国特拉华州一所小学为例，就“问题提出”如何融入数学课堂教学这一重要问题进行了分析，并得到了四点启示［92］。

8. 理论研究

173篇文献中，很少有对数学问题提出的理论研究——这与Shin-Yi Lee［93］的研究结果

相符。最具有代表性的两项理论研究已经在上述分析中提及，一项是数学“情境—问题”教学模式的构建，另一项是基于问题提出的教师专业发展路径的探索。再者，张辉蓉等［94］

对教师问题提出所需要的教学知识进行了理性探讨，从教什么、教谁和怎么教三个维度梳理出问题提出知识、学生问题提出知识、问题提出情境知识、问题提出教学方法知识、问题提出教学评估知识共同构成问题提出教学知识；张玲等［95］

构建了问题提出中数学交流的一般模式，即“问题提出任务情境→（输入）理解问题情境→（内部加工）筛选信息、重组信息→（输出）组织语言→问题”。

四、 结论与启示

本文对173篇国内外关于数学问题提出的高水平研究论文从八个维度进行了系统分析和讨论。总体而言，研究表现出三大取向：研究方法以实证研究为主的科学性取向、研究对象以小学生和职前教师为主的阶段性取向以及研究主题以教学和教师教育为主的实践性取向。具体地，可得到如下结论与启示：

第一，从文献的基础信息，即来源、年份、机构和地区及核心作者来看，国内外的研究20多年来呈现出波动增长的发展趋势，研究的热度愈来愈高，主要集中在《数学教育学报》、Educational Studies in Mathematics这两本数学教育领域的权威期刊上，中美两国的研究者贡献了重要的研究力量，并形成了以蔡金法、吕传汉和宋乃庆等为主的核心作者群，所在机构西南大学、贵州师范大学和美国特拉华大学也成为最主要的发文机构。

第二，在研究方法上，实证研究，尤其是量化研究，成为主流的方法类型，展现出较强的科学研究范式。值得注意的问题是，相较之下，国外研究方法类型更丰富，也更善于挖掘相关的文本素材，中国的研究者需要加强研究方法的创新使用。

第三，在研究对象上，学生和教师是研究者最为关注的群体，但是这些群体具有较为明显的阶段性，分布不均，因此，需要加强对小学和职前之外其他阶段学生和教师的关注。

第四，在研究主题上，教学与教师教育研究主题以压倒性的数量优势显露出国内外学者的研究兴趣，其在问题提出教学、教师专业发展等方面展现出的实践性让问题提出这一话题成为学校数学教育的垫脚石。

虽然国内外的数学问题提出研究成果颇丰，但是还存在三个较为重要的问题亟待解决：

首先，要提供各学段、各知识板块的教学实践案例。目前相关论文主要聚焦于小学阶段的“数与代数”领域，而数学教材中大部分是师生间的互动性提问，不能等同于问题提出任务。这就造成了对问题提出的理性重视与课堂教学的实践匮乏之间的落差，一线教师认识到问题提出教学的价值，但缺乏这类教学资源来支持他们进行问题提出教学。

其次，要探索更多具有普适性的基于问题提出的教学模式。目前除了“情境—问题”教学模式之外，大部分研究只是针对某一特殊问题的方法和经验总结，难以进行大范围推广。

最后，要重视对问题提出“过程”的专门研究和理论研究。前者可以更好地从心理学、哲学等视角了解教师和学生在问题提出过程中的数学思维，后者可以为其他研究的设计、分析和应用提供帮助。

参考文献：

［1］ 张玲，宋乃庆，蔡金法.问题提出：基本蕴涵与教育价值［J］.中国电化教育，2019（12）：31-39.

［2］ E.A. Silver， K. Yankson. Book review： roots and sprouts： cultivating research on mathematical problem posing［J］.Journal for Research in Mathematics Education， 2017（1）：111-116.

［3］［35］ 尚亚明，何忆捷，熊斌.中国数学问题提出研究的回顾与展望［J］.数学教育学报，2019（6）：81-86.

［4］ 陈汉君，杨蕊.近二十年我国数学问题提出研究知识图谱分析［J］.数学通报，2020（6）：10-13.

［5］［87］ 尚亚明，熊斌.数学问题提出的过程性研究述评［J］.数学教育学报，2021（5）：66-71.

［6］ 尚亚明，何忆捷，熊斌.国外数学问题提出能力影响因素的研究述评——基于学生自身的知识经验和观念系统等“变量”因素［J］.数学教育学报，2020（2）：58-63.

［7］［16］ 吕传汉，汪秉彝.再论中小学“数学情境与提出问题”的数学学习［J］.数学教育学报，2002（4）：72-76.

［8］［25］［88］ F.M. Singer， N. Ellerton， J. Cai. Problem-posing research in mathematics education：new questions and directions［J］. Educational Studies in Mathematics， 2013（1）：1-7.

［9］ J. Cai， R. Leikin.Call for papers： educational studies in mathematics special issue： affect in mathematical problem posing［J］.Educational Studies in Mathematics，2018（3）：243-244.

［10］ J. Cai， S. Hwang.Learning to teach through mathematical problem posing： Theoretical considerations， methodology， and directions for future research［J］.International Journal of Educational Research， 2020，102：101391.

［11］ 宋乃庆，张莎莎，陈婷，等.基于“问题提出”的小学数学教师主题式专业发展：理论建构与实践探索［J］.数学教育学报，2021（1）：12-18.

［12］ 苏志芳，张建中，胡惠芳.基于模糊综合评判的中文社科图书“核心作者”决策研究［J］.图书情报工作，2010（1）：42-45+41.

［13］ 张子婷，郑彦宁，袁芳.多指标核心作者识别方法研究［J］.现代情报，2020（7）：144-151.

［14］ 邱学平.信息计量学［M］.武汉：武汉大学出版社，2007：194.

［15］ 蔡金法，姚一玲.数学“问题提出”教学的理论基础和实践研究［J］.数学教育学报，2019（4）：42-47.

［17］［40］ 宋乃庆，周莞婷，陈婷，等.小学数学教师“问题提出”的教学信念研究［J］.数学教育学报，2019（4）：24-29.

［18］ 陈婷，徐红，徐冉冉，等.数学教师学习使用“问题提出”教学法的个案研究——以“用字母表示稍复杂的数量关系”为例［J］.数学教育学报，2019（2）：7-12.

［19］ 夏小刚，汪秉彝.数学情境的创设与数学问题的提出［J］.数学教育学报，2003（1）：29-32.

［20］［82］ 姚一玲，徐冉冉，蔡金法.用“问题提出”诊断和评估数学教师的概念性理解［J］.数学教育学报，2019（4）：30-36.

［21］［39］ 李欣莲，宋乃庆，陈婷，等.小学数学教师“问题提出”表现研究［J］.数学教育学报，2019（2）：1-6.

［22］ 徐冉冉，裘晓丽，姚一玲，等.基于教师—研究者伙伴关系的初中数学教学改进——以“一次函数”“问题提出教学”为例［J］.数学教育学报，2021（1）：25-31.

［23］ 陈丽敏，景敏，Verschaffel Lieven，等.五年级小学生数学问题提出能力和观念的调查研究2013（2）：27-32.

［24］［83］ R. Leikin， H. Elgrably. Problem posing through investigations for the development and evaluation of proof-related skills and creativity skills of prospective high school mathematics teachers［J］.International Journal of Educational Research， 2020，102：101424.

［26］ S. Crespo. Learning to pose mathematical problems：exploring changes in preservice teachers’ practices［J］.Educational Studies in Mathematics，2003（3）：243-270.

［27］ I. Kontorovich， B. Koichu. A case study of an expert problem poser for mathematics competitions［J］.International Journal of Science and Mathematics Education， 2016（1）：81-99.

［28］ C. Voica， F.M. Singer. Problem modification as a tool for detecting cognitive flexibility in school children［J］.ZDM- Mathematics Education， 2013（2）： 267-279.

［29］ B. Koichu， I. Kontorovich.Dissecting success stories on mathematical problem posing： a case of the billiard task［J］.Educational Studies in Mathematics， 2013（1）：71-86.

［30］ 夏小刚.国内外数学问题提出教学研究的回顾与反思［J］.数学教育学报，2005（3）：17-20.

［31］［75］ L. Headrick， A. Wiezel， G. Tarr， et al. Engagement and affect patterns in high school mathematics classrooms that exhibit spontaneous problem posing：an exploratory framework and study［J］.Educational Studies in Mathematics， 2020（3）：435-456.

［32］ 张昱城，葛林洁，张山杉，等.经验研究的新范式——经验取样法［J］.中国人力资源开发，2019 （1）：8-15+69.

［33］ M. Tichá， A. Hopesová.Developing teachers’ subject didactic competence through problem posing［J］.Educational Studies in Mathematics， 2013（1）：133-143.

［34］［57］ 李怀军，张维忠.小学生数学问题提出能力发展研究［J］.数学教育学报，2019（5）：2-8.

［36］［93］ S.Y. Lee. Research status of mathematical problem posing in mathematics education journals［J］.International Journal of Science and Mathematics Education， 2020（8）：1677-1693.

［37］ 石义娜，吴京霖，夏小刚.近十年中国数学教育研究图景——基于《数学教育学报》（2012—2022年）文献共被引的视角［J］.数学教育学报，2023（2）：88-96.

［38］ J. Cai， T. Chen， X. Li， et al. Exploring the impact of a problem-posing workshop on elementary school mathematics teachers’ conceptions on problem posing and lesson design［J］.International Journal of Educational Research， 2020，102：101404.

［41］ 张莎莎，宋乃庆，蔡金法.小学数学教师“问题提出”课堂教学行为研究［J］.数学教育学报，2022（2）：46-52.

［42］ 王加明，蔡金法.用问题提出架起学生数学思考的空间——以“百分数”复习课为例［J］.小学数学教师，2021（3）：33-37.

［43］ 徐红，蔡金法.合作学习借问题提出 问学交融促思维发展——以“用字母表示数量关系”教学为例［J］.小学数学教师，2020（2）：14-17+2.

［44］ 陈沙沙，蔡金法.合作学习中的问题提出助力概念理解——“周长”教学实践与思考［J］.小学数学教师，2020（2）：17-21.

［45］ N.F. Ellerton. Engaging pre-service middle-school teacher-education students in mathematical problem posing：development of an active learning framework［J］.Educational Studies in Mathematics， 2013（1）：87-101.

［46］ S. Crespo. Learning to pose collaborative mathematics problems with secondary prospective teachers［J］. International Journal of Educational Research， 2020，102：101430.

［47］ 吕传汉，汪秉彝.论中小学“数学情境与提出问题”的数学学习［J］.数学教育学报，2001（4）：9-14.

［48］ 吕传汉，汪秉彝.论中小学“数学情境与提出问题”的教学［J］.数学教育学报，2006（2）：74-79.

［49］ 李荣，吕传汉.“数学情境与提出问题”教学模式对缓解贵州初中生数学焦虑的探究［J］.数学教育学报，2004（4）：88-89.

［50］ 吴增生，郑燕红，吴海燕，等.怎样促进学生提出和解决高价值的数学问题——等腰三角形单元教学对比实验研究［J］.数学教育学报，2022（1）：42-51.

［51］ 桂潇爽，刘咏梅.基于问题提出能力培养的y=Asin（ωx+φ）教学［J］.中国数学教育，2018（12）：12-14+18.

［52］ 徐彦辉.数学解题后的“回顾与反思”与数学问题的提出——探索一种通过“回顾与反思”来提出数学问题的模式与方法［J］.数学教育学报，2015（1）：9-12.

［53］ 曾小平，吕传汉，汪秉彝.初中生“提出数学问题”的现状与对策［J］.数学教育学报，2006（3）：51-53.

［54］ 赵取花，汤服成.农村学校学生数学问题提出能力的现状调查与分析［J］.数学教育学报，2006（4）：69-72.

［55］ 李亚玲.初中生数学问题提出能力的表现和启示——以北京市某区初中教育质量综合评价数学测试为例［J］.中国数学教育，2019（23）：12-16+24.

［56］ 张丹，吴正宪.培养小学生问题提出能力的实证研究——以小学数学教学为例［J］.中国教育学刊，2017（5）：100-104.

［58］ 胡卫平，韩琴.小学生创造性科学问题提出能力的发展研究［J］.心理科学，2006（4）：944-946+928.

［59］ 吴华，卢小男.多媒体教学环境辅助学生提出数学问题的探索［J］.数学教育学报，2009（2）：72-75.

［60］ 张屹，董学敏，陈蓓蕾，等.智慧教室环境下的APT教学对小学生问题提出与问题解决能力的培养研究［J］.中国电化教育，2018（4）：57-65.

［61］ 王嵘，蔡金法.问题提出：从课程设计到课堂实践［J］.课程·教材·教法，2020（1）：90-96.

［62］ 陈婷，谢升梅，蔡金法.我国中小学数学课程中“问题提出”的演变——基于课程标准（教学大纲）的分析［J］.课程·教材·教法，2021（5）：82-89.

［63］ 许天来，蔡金法.美国数学课程中的“问题提出”——期望与挑战［J］.数学教育学报，2019（2）：18-23.

［64］ 郭玉峰，闫佳洁，周雯佳.问题提出融入中小学数学教科书：现状、困境及解决思路［J］.课程·教材·教法，2022（6）：117-123.

［65］ J. Cai， C. Jiang. An a_{Us2zUy79dXne331BqNtd6DxphD0i4X3ERJ8nD70m4X8=}nalysis of problem-posing tasks in chinese and US elementary mathematics textbooks［J］. International Journal of Science and Mathematics Education， 2017（8）：1521-1540.

［66］ 胡典顺，薛亚乔，王明巧.中国和美国小学数学教材中问题提出的比较研究［J］.数学教育学报，2016（4）：37-41.

［67］ 严卿，胡典顺.中国和日本初中数学教材中问题提出的比较研究［J］.数学教育学报，2016（2）：20-25.

［68］ 宋运明，夏小刚，张学杰.对小学数学教科书中“提出问题”提示语编写的思考和建议——基于四种版本教科书的统计与分析［J］.课程·教材·教法，2011（4）：52-57.

［69］ 胡典顺，蔡金法，聂必凯.数学问题提出与课程演变：两个版本小学数学教材的比较［J］.课程·教材·教法，2015（7）：75-79+36.

［70］ S. Jia， Y. Yao. 70 Years of problem posing in Chinese primary mathematics textbooks［J］.ZDM–Mathematics Education， 2021（4）：951-960.

［71］ E.A. Silver， J. Cai. An analysis of arithmetic problem posing by middle school students［J］.Journal for Research in Mathematics Education， 1996（5）：521-539.

［72］ 陈丽敏，Lieven Verschaffel，李雪梅.问题提出和问题解决之间关系的问卷调查［J］.数学教育学报，2004（4）：67-71.

［73］ L. Zhang， J. Cai， N. Song， et al. Mathematical problem posing of elementary school students：the impact of task format and its relationship to problem solving［J］.ZDM–Mathematics Education， 2022（3）：497-512.

［74］ M. Guo， F.K.S. Leung， X. Hu. Affective determinants of mathematical problem posing： the case of Chinese Miao students［J］. Educational Studies in Mathematics， 2020（3）：367-387.

［76］ 张丹，姚一玲，蔡金法.问题提出教学对学生数学成绩和数学情感影响的实验研究［J］.数学教育学报，2021（1）：32-36.

［77］ 夏小刚，汪秉彝，吕传汉.中小学生提出数学问题能力的评价再探［J］.数学教育学报，2008（2）：8-11.

［78］ O. Cankoy， H. zder. Generaliza-bility theory research on developing a scoring rubric to assess primary school students’ problem posing skills［J］.Eurasia Journal of Mathematics， Science and Technology Education， 2017（6）：2423-2439.

［79］ J. Cai， J.C. Moyer， N. Wang， et al.Mathematical problem posing as a measure of curricular effect on students’ learning［J］. Educational Studies in Mathematics， 2013（1）：57-69.

［80］ A. Bicer， Y. Lee， C. Perihan， et al. Considering mathematical creative self-efficacy with problem posing as a measure of mathematical creativity［J］.Educational Studies in Mathematics， 2020（3）：457-485.

［81］ 宋乃庆，胡睿，蔡金法.用问题提出和问题解决测试小学生对平均数的理解［J］.数学教育学报，2020（3）：1-8.

［84］ C. Christou，N. Mousoulides， M. Pittalis， et al. An empirical taxonomy of problem posing processes［J］.ZDM-Mathe-matics Education， 2005（3）：149-158.

［85］ L. Baumanns， B. Rott. The process of problem posing： development of a descriptive phase model of problem posing［J］.Educational Studies in Mathematics， 2021（2）：251-269.

［86］ L. Baumanns. Identifying metacognitive behavior in problem-posing processes：development of a framework and a proof of concept［M］//Mathematical Problem Posing： Conceptual Considerations and Empirical Investigations for Understanding the Process of Problem Posing. Wiesbaden： Springer Fachmedien Wiesbaden， 2022：189-223.

［89］ 李怀军，张维忠.国外“数学问题提出教学法”研究：回顾与前瞻［J］.浙江师范大学学报（自然科学版），2020（1）：107-114.

［90］ 陈婷，李兰，蔡金法.中国小学数学“问题提出”教学的研究与实践——基于《小学数学教师》和《小学教学》（数学版）中“问题提出”文章的分析［J］.数学教育学报，2021（1）：19-24.

［91］ 于文华.美国数学问题提出：是非与评述［J］.数学教育学报，2018（2）：24-28.

［92］ 于文华，蔡金法，刘美玲，等.美国小学数学教学中的问题提出及启示——以West Park Place Elementary School为例［J］.数学教育学报，2018（5）：61-65.

［94］ 张辉蓉，冉彦桃，刘蝶，等.教师“问题提出”教学知识建构［J］.数学教育学报，2019（2）：13-17.

［95］ 张玲，宋乃庆，蔡金法.问题提出中数学交流的模式构建与案例解析［J］.数学教育学报，2019（4）：37-41.

（张慕橙，北京师范大学中国基础教育质量监测协同创新中心。主要研究方向：数学教育。

夏小刚，贵州师范大学数学科学学院，教授，博士生导师。主要研究方向：数学教育。）