基于GPR模型的多孔沥青混合料空隙率预估

摘 要：多孔沥青混合料空隙率是影响其排水功能和路用性能的关键指标之一。为实现多孔沥青混合料空隙率的快速判别，该研究以混合料级配不同筛孔尺寸通过率、油石比为自变量，通过相关性分析提取特征参数，进而基于高斯过程回归（GPR）模型建立PAC-13多孔沥青混合料空隙率预估模型，并对比分析GPR模型与多元线性回归、AdaBoost和随机森林法对多孔沥青混合料空隙率的预估准确性。结果表明，以4.75、2.36、1.18、0.6、0.3、0.15和0.075 mm的筛孔通过率，以及油石比作为模型参数的多孔沥青混合料空隙率GPR预估模型具有较好的准确性，线性拟合系数达到0.95;相比多元线性回归、AdaBoost和随机森林法，GPR模型对于多孔沥青混合料空隙率预估的适用性相对更优。

关键词：道路工程;多孔沥青混合料;空隙率;高斯过程回归;预估模型

中图分类号：U416.2 文献标志码：A 文章编号：2095-2945（2024）30-0052-04

Abstract： The void content of porous asphalt mixture is one of the key indicators that affect its drainage function and road performance. In order to quickly determine the void content of porous asphalt mixtures， this study took the passage rate of different sieve size and oil-stone ratio of the mixture gradation as independent variables， extracted characteristic parameters through correlation analysis， and then established the PAC-13 porous asphalt mixture void content prediction model based on the Gaussian Process Regression（GPR） model， and compared and analyzed the accuracy of the GPR model with multiple linear regression， AdaBoost and random forest methods in predicting the void content of porous asphalt mixtures. The results show that the GPR model for predicting the porosity of porous asphalt mixtures AjUERXQ36NKkKcmYyebCbw==using the sieve passage rates of 4.75 mm， 2.36 mm， 1.18 mm， 0.6 mm， 0.3 mm， 0.15 mm and 0.075 mm and oil-to-stone ratio as model parameters has good accuracy， with a linear fitting coefficient of 0.95; compared with multiple linear regression， AdaBoost and random forest methods， the GPR model is relatively more applicable to predicting the porosity of porous asphalt mixtures.

Keywords： road engineering; porous asphalt mixture; void content; Gaussian Process Regression （GPR）; prediction model

多孔沥青混合料（Porous Asphalt Concrete， PAC）是一种绿色型路面材料，在不同的国家和地区也被称为排水路面材料，开级配磨耗层（Open Graded Friction Course， OGFC），大空隙沥青混合料。因混合料内部含有较多的空隙与连通空隙，其排水、抗滑、降噪、防眩光、防水溅功能显著，在国内外高等级公路得到广泛应用。目前，关于多孔沥青混合料内部空隙的研究主要分为2种：内部空隙分布特征及其相关影响因素;内部空隙识别精度及空隙对宏观性能的影响规律，也有研究多孔沥青碎石材料的渗透系数预估模型[1]，但对空隙率预估模型研究较少，且预估模型是基于传统概率统计方法[2]，预估精度并未体现。同时，高斯过程回归模型应用于多孔沥青混合料的相关研究较少。因此，本文依据关键筛孔和油石比对空隙率的影响规律，选定合理参数，基于高斯过程回归建立多孔沥青混合料PAC-13的空隙率预估模型，对模型的有效性进行评价和分析。

1 基于GPR的空隙率预估模型构建

1.1 数据预处理及预估评估参数

1.1.1 数据来源

本文数据来自公开发表的文献，共包含62组PAC-13试样的组成和空隙特征数据[2-13]。PAC-13多孔沥青混合料均为击实次数50次的标准马歇尔试件，11个输入变量包括多孔沥青混合料在不同孔径下的筛孔通过率和油石比，输出变量为空隙率。

1.1.2 相关性分析

采用皮尔逊相关系数法分别计算了不同孔径下的筛孔通过率和油石比与空隙率的相关系数，并计算出各个变量的特征重要性。由表1可知，筛孔尺寸为13.2 mm和9.5 mm的皮尔逊相关系数的绝对值小于0.2，当相关性系数小于0.2时，可认为已基本不相关;筛孔尺寸为2.36 mm的相关系数绝对值在所有筛孔尺寸中最高，说明其对空隙率影响较大。因此，对于多孔沥青混合料PAC-13的空隙率预估模型，本文剔除了筛孔尺寸为13.2 mm和9.5 mm的数据，选取其他几个变量作为预测模型的输入因子。将剩余变量作为输入因子预测效果更好，这与已有研究结论相一致[14]。

1.1.3 数据归一化及评估参数

1）归一化处理。为保证样本数据量纲统一，采用最大值和最小值归一化公式对样本数据进行归一化处理，其表达式如下所示

X= ， （1）

式中：Xmin、Xmax为分别为每条时间序列数据中的最小值和最大值;Xi为第i个监测值;X为归一化后处理之后的数据。

2）模型参数重要性评估。为了有效评估模型的预测精度，采用均方误差（Mean Square Error，MSE）、平均绝对误差（Mean Absolute Error， MAE）、拟合优度（R2）3种基本指标。指标计算方法为

MSE=∑（yi-ι）2 ， （2）

MAE=∑（yi-ι） ，（3）

R2=1- ， （4）

式中：m为测试集中的样本数;yi、ι、ι为分别是真实值、预测值和真实值的平均值。

1.2 空隙率预估模型构建

1.2.1 GPR模型原理

高斯过程回归（Gaussian Process Regression， GPR）是使用高斯过程（Gaussian Process， GP）先验对数据进行回归分析的非参数模型，通过有限的高维数据来拟合出相应的高斯过程，从而预测任意随机变量下的函数值。高斯过程是定义在连续域上的无限多个服从高斯分布的随机变量组成的随机过程。GPR模型在使用时，不需要指出具体的输出形式，只需将n维训练集所对应的关系（y1，y2，…，yn）作为高斯分布的一个n维采样点[15]。

对于受噪声污染的回归方程

y=f（x）+ε～N（μ（x），K（x，x）+σ2I） ， （5）

式中：f（x）为回归方程，ε～N（0，σ2）为随机噪声，I为长度尺度向量。

由此可以得到，任意一点处的高斯过程训练集训练值f和训练输出值f*的先验公式

ff *～N0，（K（x，x）+σ2I K（x，x） K（x，x） K（x，x）=N0，K KKK， （6）

式中：K（x，x）是输入样本x的协方差矩阵，K是输入样本x与待预测输入值x之间的协方差矩阵，K是待预测输入值x的方差。

高斯过程的后验分布公式为

f *|x，y，x*～N，covf * ， （7）

式中

≌E[f *|x，y，x*]=k（x*，x）[k（x，x）+σ2I]-1y ，（8）

cov（f *）=k（x*，x*）-k（x*，x）[k（x，x）+σ2I]-1k（x，x*）。（9）

1.2.2 GPR建模流程

高斯过程（GP）是一种具有高度表现力的监督学习算法。由相关性分析结果选定4.75、2.36、1.18、0.6、0.3、0.15和0.075 mm关键筛孔通过率，以及油石比作为输入因子，空隙率为输出因子。基于有限的数据集，将数据集合按照70%和30%的分配比例划分为训练集和测试集。

2 GPR模型结果评价与分析

2.1 GPR模型预测结果与评价

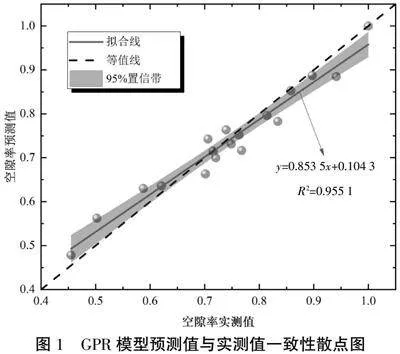
图1为基于GPR模型对多孔沥青混合料的空隙率预测值与实测值的拟合结果。从图1可知，尽管存在一定程度偏离等值线的散点，大多预测点均能够稳定地分布在中心区域左右，其线性拟合值达到0.95，说明预测值与真实值非常接近，具有良好一致性，反映了GPR模型可有效预估多孔沥青混合料的空隙率。

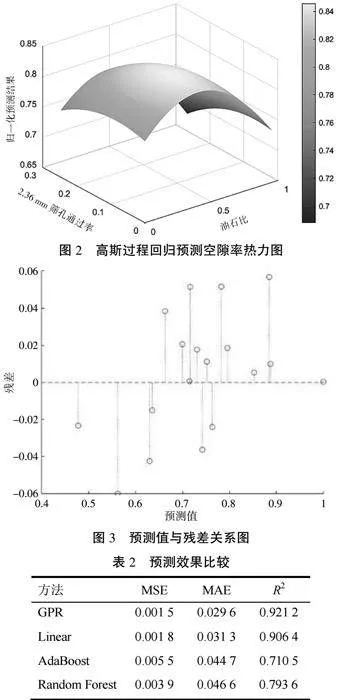
图2为高斯过程回归预测空隙率结果热力图，数据及结果均经过归一化处理。由前文相关性结果可知，2.36 mm筛孔通过率与空隙率相关性最高，油石比与空隙率也有密切联系。故以上述2个特征参数输入，空隙率预测归一化结果为输出。图2直观反映了多孔沥青混合料PAC-13的空隙率随关键筛孔2.36 mm通过率及油石比的变化趋势。其中，空隙率预测归一化结果值随2.36 mm筛孔通过率的增大而减小，随油石比的含量增大而减小。

对多孔沥青混合料空隙率预测值与真实值进行误差计算，结果如图3所示，测试集误差大致服从正态分布，且大部分误差都位于（-0.06～+0.06），说明通过GPR模型预测的空隙率与真实空隙率之间误差微小，模型结果具有较高准确性。

2.2 GPR与其他模型预测效果比较

为验证高斯过程回归方法对空隙率预测效果的有效性，将其与多元线性回归、AdaBoost、随机森林预测方法进行了比较。采用4种方法预测得到模型评价指标结果见表2。从表2可以看出，在整个预测集数据段内，采用高斯过程回归方法预测的MSE和MAE均小于多元线性回归、AdaBoost和随机森林回归方法所预测的，说明基于高斯过程回归的多孔沥青混合料空隙率预测方法比其他3种预测方法更有效。且文中采用预测模型R2最大，为0.921 2，说明GPR模型拟合效果好。综合表明，GPR模型预测精度高、可解释性好。

3 结论

1）以4.75、2.36、1.18、0.6、0.3、0.15和0.075 mm的筛孔通过率、油石比、空隙率为模型参数，建立了多孔沥青混合料PAC-13的空隙率预测模型，拟合决定系数达到0.92，说明GPR模型的精确性与优越性。

2）采用残差对预测结果和真实结果进行对比分析，大部分误差都位于（-0.06～+0.06）的区间，说明GPR的预测结果准确度高。

3）不同预测模型之间预测结果存在明显差异，对比可知采用GPR模型预测的结果均方误差和平均绝对误差较其他模型更小，拟合优度更高，可解释性好。

参考文献：

[1] ELASYED AS， LINDLY JK. Estimating Permeability of Untreated Roadway Bases[J]. Transportation Research Record，2010，1519：11-18.

[2] 蒋玮，沙爱民，肖晶晶，等.多孔沥青混合料PAC-13空隙率预估模型[J].武汉理工大学学报，2011，33（11）：55-59.

[3] 李翔，蔡旭，肖天佑.排水路面沥青混合料的连通空隙影响分析[J].华侨大学学报（自然科学版），2019，40（2）：186-191.

[4] 方涛.多孔沥青混合料路表功能的平衡设计[D].哈尔滨：哈尔滨工业大学，_{66384b39cc72297df16a16241e40954ba52743b414c5e3896635bde6eec3f229}2019.

[5] 罗凯，张云霞，邓娟华，等.空隙特征对排水路面残留饱水度的影响[J].公路，2021，66（8）：49-55.

[6] 裴建中，张嘉林，常明丰.矿料级配对多孔沥青混合料空隙分布特性的影响[J].中国公路学报，2010（1）：1-6.

[7] 蒋玮，沙爱民，裴建中，等.多孔沥青混合料的疲劳特性试验研究[J].建筑材料学报，2012，15（4）：513-5d89687f624b95d9f11edbfa29463f7c382e4f4bc20746a93dce8e09957470e5517.

[8] 李金凤，何兆益，官志桃.多孔沥青混合料矿料间隙率物理模型的构建[J].哈尔滨工业大学学报，2022，54（3）：139-147.

[9] 基敏雪，王宏畅.基于数字图像处理技术的多孔沥青混合料细观空隙特征规律[J].中外公路，2018，38（5）：257-261.

[10] 任天琦.不同成型方法对多孔沥青混合料细观结构和路用性能的影响[D].哈尔滨：东北林业大学，2023.

[11] 吴江涛.基于多孔沥青混合料强度特性的透排水路面结构设计[D].南京：东南大学，2017.

[12] 杨旋.高黏改性沥青性能及其混合料细观空隙特征研究[D]. 重庆：重庆交通大学，2021.

[13] 蒋玮.透水沥青路面材料和结构的组成设计与功能评价[D].西安：长安大学，2011.

[14] 肖晶晶，沙爱民，蒋玮.多孔沥青混合料空隙率与关键筛孔相关性研究[J].武汉理工大学学报，2010，32（12）：29-32.

[15] 宁慧员，张菊，闫长旺，等.基于高斯过程回归模型的电石渣激发煤矸石地聚合物强度响应预测与分析[J].硅酸盐通报，2024，43（3）：905-913.

基金项目：云南省大学生创新创业训练计划项目（S202210674133）;云南省教育厅科学研究基金项目（2023J0132）

第一作者简介：马志鹏（2000-），男，硕士研究生。研究方向为道路工程。

*通信作者：刘祥（1990-），男，博士，讲师。研究方向为绿色与数智道路基础设施。