灵活运用多种方法填聪明数格

小朋友，前几期中，我们介绍了一些填聪明数格的技巧。“已知数”“特殊的结果”等都是填写这类谜题的突破口。下面，我们一起来学习填写6×6混合聪明数格的方法。

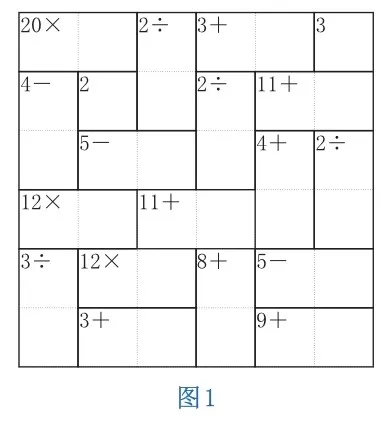
例题图1 是一个6 ×6的混合聪明数格。你能在空格内填入1 ～6 ，使得每个数在每行、每列中都不重复，且每个实线框中左上角的数正好是这个框中其他数的和、差、积或商吗？

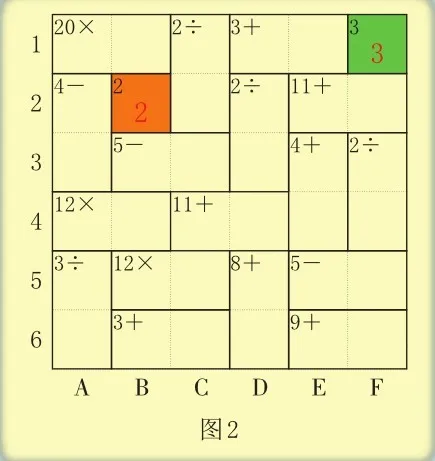
为了便于叙述，我们可以像图2这样标注方格所在的列和行，用字母与数的组合来表示方格的位置，如橙色方格可以记为B2，绿色方格可记为F1。这道题有两个已知数，B2填2，F1填3。

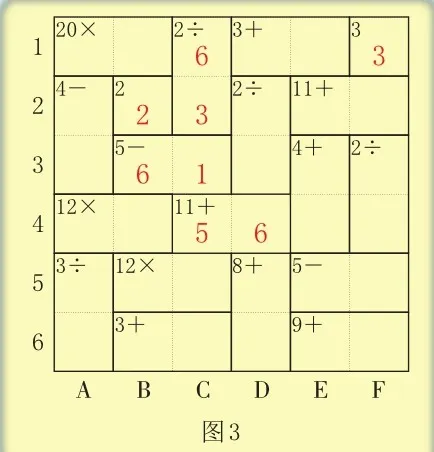
第1行的和3只能是1+2=3，和3所在框中的两个数是1和2。第1行的积20只能是4×5=20，积20所在框中的两个数是4和5。根据每行中的数不重复，第1行中已经有1，2，3，4，5，可知C1填6。根据C列中的商2可知，C2填6÷2=3。第3行中的差5只能是6-1=5，差5所在框中的两个数是1和6，因为C列中已经有了6，所以B3填6，C3填1。第4行中的和11只能是5+6=11，和11所在框中的两个数是5和6，因为C列中已经有了6，所以C4填5，D4填6（如图3）。

第6行中和3所在框中的两个数只能是1和2，因为C列中已经有了1，所以B6填1，C6填2。根据每列中的数不重复，C列中已经有1，2，3，5，6，可知C5填4。根据第5行中的积12可知B5填12÷4=3。D列中的和8可能是2+6=8，也可能是3+5=8，和8所在框中的两个数可能是2和6，也可能是3和5。因为D列中已经有了6，所以和8所在框中的两个数只能是3和5，又因为第5行中已经有了3，所以D5填5，D6填3（如图4）。

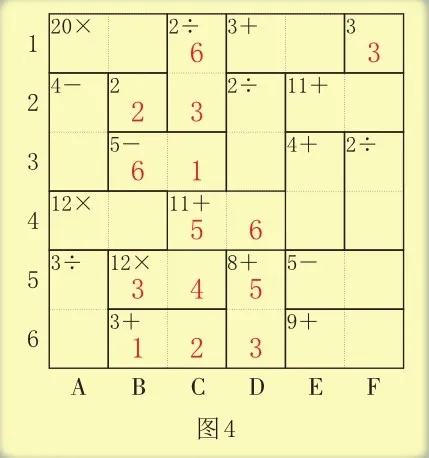
这时，B列中剩下未填的数是4和5，因为第4行的积12不是5的倍数，所以B1填5，B4填4。根据第1行中的积20可知，A1填 20÷5=4。根据第4行中的积12可知A4填12÷4=3。D列中剩下未填的数是1，2，4，其中满足商是2的有2÷1=2和4÷2=2，商2所在框中的两个数可能是1和2，也可能是2和4。因为第1行中和3所在框中的两个数只能是1和2，且D列中已经有了2，所以D1填1，E1填2。D列中商2所在框中的两个数只能是2和4，又因为第2行中已经有了2，所以D2填4，D3填2（如图5）。

E列中的和4只能是1+3=4，和4所在框中的两个数是1和3。因为第4行中已经有了3，所以E3填3，E4填1。第2行中和11所在框中的两个数只能是5和6。因为第2行中已经有了2，3，4，5，6，所以A2填1。根据A列中的差4可知A3填1+4=5。根据唯一法可知，A列中剩下两个空格中的数是2和6，因为第6行中已经有了2，所以A5填2，A6填6。根据唯一法可知，F3填4，F4填2（如图6）。

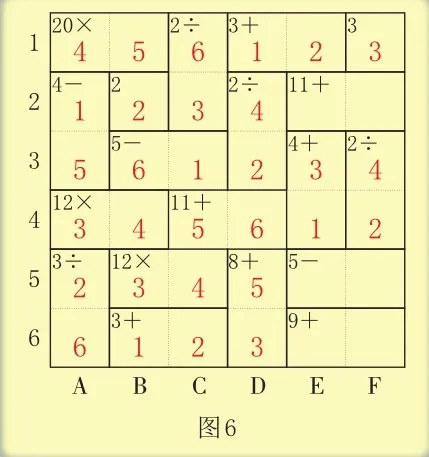
根据唯一法可知，第5行剩下两个空格中的数是1和6，因为E列中已经有了1，所以E5填6，F5填1。根据唯一法可知，第6行剩下两个空格中的数是4和5，因为F列中已经有了4，所以E6填4，F6填5。根据唯一法可知，E2填5，F2填6。最终的答案如图7所示。

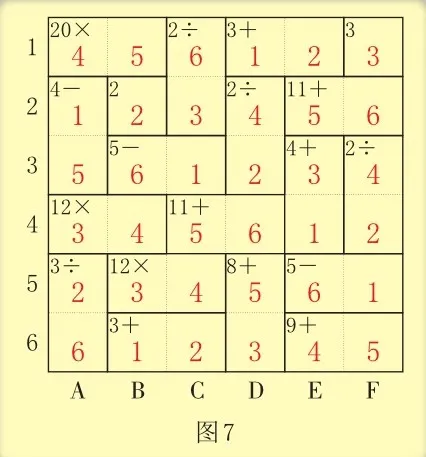
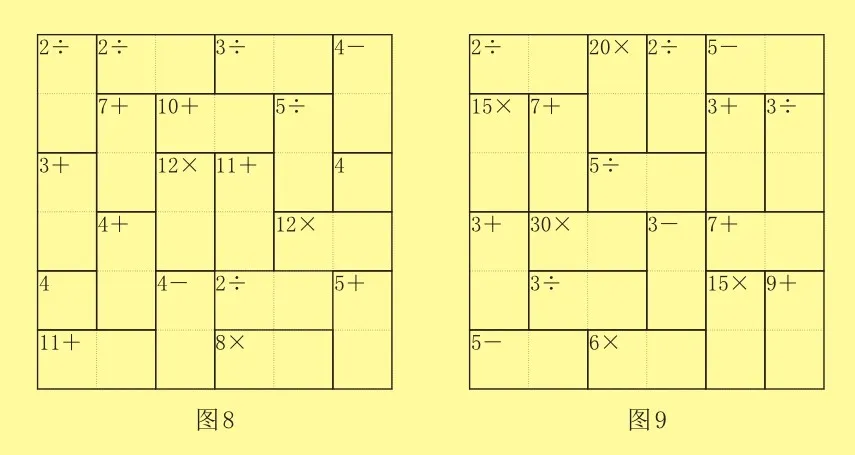
小朋友，下面你来填一填图8、图9的6×6混合聪明数格吧！

填写要求：在空格内填入1～6，使得每个数在每行、每列中都不重复，且每个实线框中左上角的数正好是这个框中其他数的和、差、积或商。