基于模糊神经网络的挖掘机发动机故障智能诊断方法

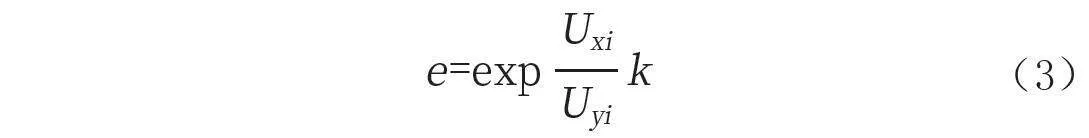
摘要：从基于模糊理论的发动机状态关联分析、基于神经网络的发动机故障诊断研究等两个方面，阐述了挖掘机发动机故障智能诊断方法，将本文设计的挖掘机发动机故障智能诊断方法与其他两种故障诊断方法在同等测试环境下进行模拟测试，并将模拟测试得出的数据进行分析，分析结果表明本文设计的发动机故障智能诊断方法，明显优于其他两种故障诊断方法。

关键词：模糊神经网络；挖掘机发动机；故障智能诊断

0 引言

挖掘机发动机零部件众多，故障诊断繁琐。挖掘机的复杂工况和大负荷工作状态，增加了其发动机发生故障的可能性。

在挖掘机运行时间逐渐增加的客观条件下，其发动机的工作性能会出现衰退，故障率会提高，可靠性会降低[1]。及时发现并解决发动机存在的故障，对提高挖掘机工作效率、保障施工进度具有重要的现实意义。

针对发动机故障诊断问题，文献[2]将融合卷积Transformer引入到发动机故障诊断的研究中，该方法在一定程度上提高了诊断的准确性，但是其精准程度受客观因素的影响较为明显；文献[3]充分利用自适应乌鸦搜索算法的优势，设计了一种发动机故障诊断方法，并实现了提高诊断精度的目的，但是其准确性的波动较为明显。

对挖掘机发动机进行实时、有效的故障诊断，可及时发现故障部位，可减少发动机故障率，可避免或减少因其故障导致的停工和事故，也是降低维修成本的重要手段之一[4]，因此对其进行进一步研究仍然具有重要的现实意义。

为此，本文研究了基于模糊神经网络的挖掘机发动机故障智能诊断方法，并通过对比测试的方法，分析该诊断方法的实用性能。

1 挖掘机发动机故障智能诊断方法

1.1 基于模糊理论的发动机状态关联分析

由于挖掘机发动机的实际运行工况不存在唯一性，这就导致直接利用相关参数的具体取值结果对其故障状态进行诊断时的误差相对较大[5]。为此，首先分析了发动机状态关联，并在具体的分析过程中引入模糊理论[6]。

在描述挖掘机发动机故障隶属度时，主要采用了模糊集合表示法，通过这样的方法，使挖掘机发动机故障现象和故障原因实现融合[7]。其中，挖掘机发动机故障原因模糊集合可以表示为下列公式：

N={Uyi} （1）

式（1）中：N表示挖掘机发动机故障原因模糊集合；Uyi表示y故障原因和i故障原因之间的隶属度参数。挖掘机发动机故障现象模糊集合可以表示为下列公式：

M={Uxi} （2）

式（2）中：M表示挖掘机发动机故障现象模糊集合，Uxi表示x故障现象和i故障现象之间的隶属度参数。

对挖掘机发动机而言，在上述基础上充分考虑了故障原因和故障现象之间相互关联关系[8]，也就是式（1）和式（2）之间的模糊准则，借助模糊理论中的“if-then”规定，建立了挖掘机发动机故障原因和故障现象之shimE6GDhtB35VmDwV13hg==间的关联关系，其具体的规定是“ifUyi，thenUxi”。按照上述方法，实现对发动机状态关联的分析，为后续的故障诊断提供基础。

1.2 基于神经网络的发动机故障诊断研究

在完成挖掘机发动机状态关联分析后，转入对其发动机进行故障诊断研究。在进行挖掘机发动机故障诊断的研究中，引入了神经网络。

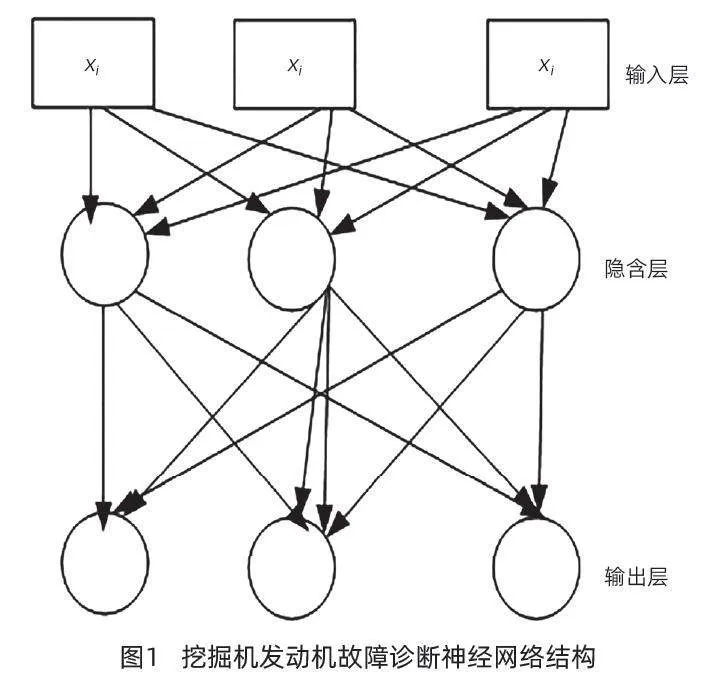
在神经网络中对训练样本进行正向计算时，设置数据的输入起点为神经网络的输入层，对应的终点为神经网络的输出层。

通过这样的方法，使得所有训练数据都能够流经BP神经网络的全部结构。在此基础上，上一层的输入与相关模型的参量就可以作为神经网络每一层各个神经元激活的具体参数，实现对故障表现与故障状态的准确诊断。本文设计的挖掘机发动机故障诊断神经网络结构示意如图1所示。

根据图1所示的挖掘机发动机故障诊断神经网络结构，在分析挖掘机发动机故障原因模糊集合与挖掘机发动机故障现象模糊集合时，为了最大限度降低诊断结果的误差，本文采用梯度下降法对挖掘机发动机故障诊断神经网络输出的故障诊断结果进行修正，具体的处理方法可以表示为下列公式：

（3）

式（3）中：e表示挖掘机发动机故障诊断神经网络输出的故障诊断结果修正值；k表示梯度下降法对挖掘机发动机故障诊断神经网络输出的故障诊断结果的修正系数。

需要特别注意的是，由于采用本文设计的方法开展挖掘机发动机故障诊断时，并未对具体的运行参数值进行分析，而是直接利用参数之间的关系进行的，因此对客观参数阈值范围的控制是关键之一。

按照上述方法，借助神经网络实现对挖掘机发动机故障的有效诊断，最大限度保障诊断结果的可靠性。

2 对诊断方法的测试

2.1 测试环境

本文以涡扇发动机为基础开展模拟测试。模拟测试以公开的涡扇发动机 C-MAPSS 数据集作为基准数据，以混合故障模式数据集作为诊断目标。

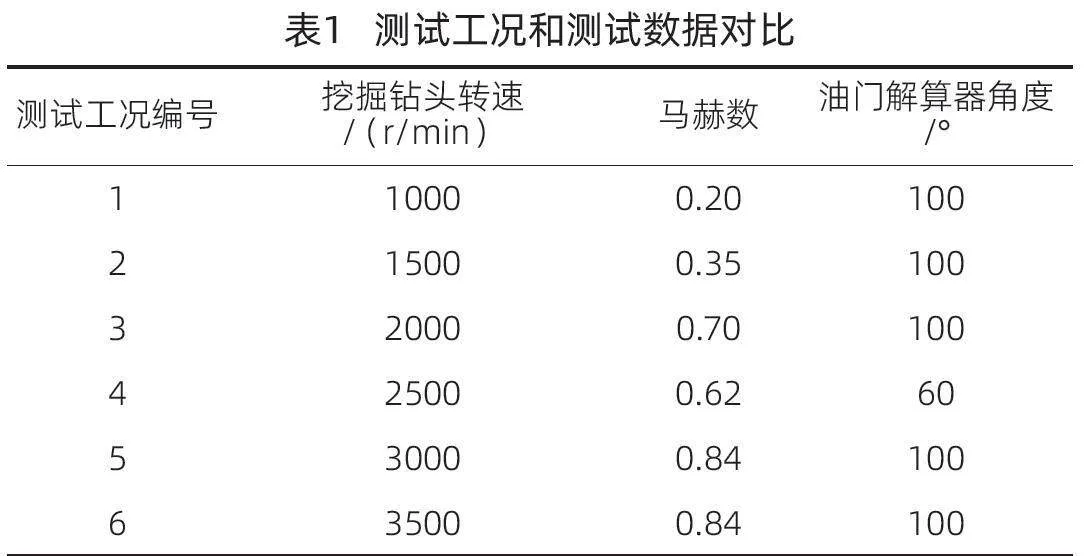
在具体测试过程中，考虑到挖掘机发动机的实际运行状态可能存在较为明显的差异，为了能够更加综合、全面地分析所设计诊断方法的应用性能，本文将分别将挖掘钻头转速V、马赫数Ma和油门解算器角度TRA作为自变量参数，设置不同的工况，以此实现对不同挖掘机发动机运行环境条件的模拟测试。测试工况和测试数据对比如表1所示。

2.2 测试方法

以上述的测试工况设置情况为基础，分别采用文献[2]提出的以融合卷积Transformer为基础的发动机故障诊断方法、文献[3]提出的以自适应乌鸦搜索算法为基础的发动机故障诊断方法和本文设计的发动机故障诊断方法，开展对比诊断模拟测试。对发动机故障诊断结果的评价，本文共设置了3个应用较广的指标作为评价基准，分别为精确率、召回率以及准确率。

2.3 测试结果

2.3.1 文献诊断方法测试结果

在上述测试环境的基础上，分别对3种不同故障诊断方法进行了测试，并将测试数据进行了记录。采用文献[2]提出的以融合卷积Transformer为基础的发动机故障诊断方法的测试结果如表2所示。采用文献[3]提出的以自适应乌鸦搜索算法为基础的发动机故障诊断方法的测试结果如表3所示。

2.3.2 本文设计诊断方法测试结果

采用本文设计的发动机故障诊断方法进行测试的结果如表4所示。

2.4 测试结果分析和结论

YQyXbrSeAfZoQmXSTfJGxg==上述3种不同故障诊断方法测试结果的数据可以发现，在不同的工况下，其表现出的诊断性能存在较为明显的差异。

在融合卷积Transformer诊断方法测试结果的数据中，在不同工况下对故障诊断的召回率始终稳定在80.0%以上，对应的准确率也达到了81.0%以上。但是精准率的波动程度较为明显，其最大值达到了95.12%（测试工况3），最小值仅为75.33%（测试工况2）。

在自适应乌鸦搜索诊断方法测试结果的数据中，在不同工况下对故障诊断的精准率和召回率均处于相对较高的状态。但是准确率稳定性偏低，其对应的最大值和最小值分别为92.46%（测试工况6）和70.15%（测试工况4）。

相比之下，在本文设计诊断方法测试结果的数据中，在设置的6种不同工况下，对于故障的诊断效果始终表现出了较高的水平，对应的精准率始终稳定在90.0%以上。其中召回率YQyXbrSeAfZoQmXSTfJGxg==始终稳定在95.0%以上，准确率始终稳定在91.0%以上。

综合上述测试数据分析可以得出以下结论：本文设计的基于模糊神经网络的挖掘机发动机故障智能诊断方法，其精准率、召回率和准确率均很高，可以实现对发动机故障状态的有效诊断，几乎不受发动机客观运行状态的影响。

3 结束语

在挖掘机发动机故障诊断过程中，由于发动机客观运行状态的差异性，导致采用单一标准对其进行诊断时，对应的诊断效果难以满足实际应用需求。本文提出的基于模糊神经网络的挖掘机发动机故障智能诊断方法，利用模糊理论和神经网络对挖掘机发动机状态进行客观分析，实现了对不同运行工况下发动机故障的有效诊断。希望本文的设计与研究，能够为挖掘机发动机故障诊断提供有价值的参考。

参考文献

[1] 陈泽灏，陈晖，高玉闪，等.基于模型的液体火箭发动机故障诊断技术研究回顾与展望[J/OL].航空学报，2023， 7（14）：1-22.

[2] 赵洪利，杨佳强.基于融合卷积Transformer的航空发动机故障诊断[J/OL].北京航空航天大学学报，2023， 2（6）：1-14.

[3] 王亮，唐明伟.自适应乌鸦搜索算法改进深度置信网络的发动机故障诊断[J].机械强度，2023，45（2）：278-283.

[4] 周寒，莫李平，刘渊，等.基于特征优化与改进KNN的航空发动机故障诊断[J].航空计算技术，2023，53（2）：45-49.

[5] 伍济钢，文港，杨康.改进一维卷积神经网络的航空发动机故障诊断方法[J].电子测量与仪器学报，2023， 37（3）：179-186.

[6] 陈财森，胡海荣，程志炜，等.基于BA-RVM算法的发动机故障诊断技术研究[J].计算机工程与科学，2023， 45（2）：332-337.

[7] 白雲杰，贾希胜，梁庆海，等.基于PCA-EDT-CNN的柴油发动机故障诊断方法[J].机械强度，2022，44（6）：1271-1278.

[8] 曹惠玲，成宝荣.基于SelBagging算法的CFM56-7B发动机故障诊断[J].中国民航大学学报，2022，40（6）：18-23.