动力学问题“两点一线”思维模式研究


功能关系是高中物理内容,其思维方法贯穿整个高中物理学习过程,是教学的难点和重点,因此牢固确立功能关系物理思维模式是学好高中物理的关键之一.利用功能关系解题的思维过程,培养并增强学生解题思维的自我调控意识,把学生解题全流程看作“获取信息—思维启动—思维逻辑—思维深化”的过程.其中与物理规律相衔接的思维逻辑的形成是解题能力提升的关键.
在功能关系解题思维模式中,涉及两种重要的物理规律,即机械能守恒定律、动能定理,还通常会与牛顿运动定律和运动规律相结合.研究物理规律的特点,探究以物理规律为载体的物理思维模式,能够简化思维流程,提升分析问题和解决问题的能力.
1 机械能守恒定律的“两点一线”思维模式
机械能守恒定律的内容是:只有重力或弹力做功的物体系统内,动能和重力势能(弹性势能)可以相互转换,而总的机械能保持不变.在利用机械能守恒定律解题时,在思维流程上,应该重点关注两个环节:一是分析过程是否符合机械能守恒的条件,二是根据研究问题的需要,确定始末状态.这一思维模式可以总结为“看一线、定两点”.
1)“看一线”就是根据守恒条件和过程的特点进行分析,互相佐证,准确判定过程是否符合机械能守恒定律.
a)守恒条件:只有重力或弹力做功.只有重力或弹力做功,并不是要求物体只受重力或弹力,此条件可以分解为三种情况:① 物体在运动过程中只受重力或弹力;② 物体在运动过程中除了受重力或弹力外,还受其他力,但其他力不做功;③ 物体在运动过程中除了受重力或弹力外,还受其他力,其他力也做功,但其他力做功的代数和为零.
b)过程特点:动能和势能互相转化.在此过程中,只有动能和重力势能或弹性势能相互转化,如果参与转化的能量还涉及热能或电势能,则机械能一般不守恒.过程特点也可以显示机械能是否守恒,如果过程中仅有动能和势能的转化,没有其他能量参与(没有能量的损失,也没有注入能量),则机械能一定守恒.
2)“定两点”即确定研究起点和终点.根据机械能守恒定律的结论:起点和终点的机械能保持不变.在解题中通常用到下面的表达形式:
1/2mv22+mgh2=1/2mv21+mgh1,
或
mgh1-mgh2=1/2mv22-1/2mv21
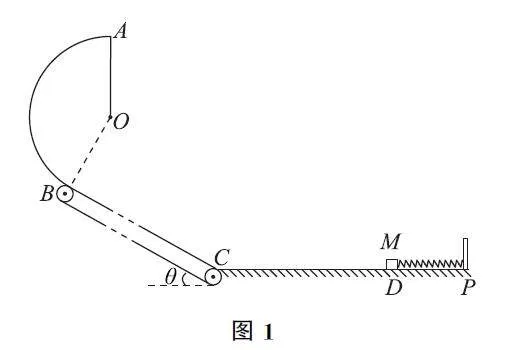
例1 如图1所示,电动机带动倾角为θ=37°的传送带以v=8ms-1的速度逆时针匀速运动,传送带下端点C 与水平面CDP 平滑连接,B、C 间距L =20m,传送带在上端点B 恰好与固定在竖直平面内的半径为R=05m 的光滑圆弧轨道相切,一轻质弹簧的右端固定在P 处的挡板上,质量M =2kg可看作质点的物体靠在弹簧的左端D 处,此时弹簧处于原长,C、D 间距x=1m,PD 段光滑,DC 段粗糙.
现用M 压缩弹簧一定距离后由静止释放,M 经过DC 冲上传送带,经B 点冲上光滑圆孤轨道,通过最高点A 时对A 点的压力为8N.上述过程中,M 经C 点滑上传送带时,速度大小不变,方向变为沿传送带方向.已知M 与传送带间的动摩擦因数为μ1 =08,与CD 段间的动摩擦因数为μ2=05,重力加速度g 取10ms-2.求:
(1)在圆弧轨道的B 点时物体的速度;
(2)M 在传送带上运动的过程中,带动传送带的电动机由于运送M 多输出的电能E;
.

