借数学之“手”，破物理难题

【摘要】解题教学是高中物理课程教学的重要组成部分，学生解题能力的提升是一线教师关注的焦点话题.本文从高中物理解题视角出发，重点剖析用数学思维解决物理问题的具体方法与手段，以期实现物理难题的突破，进而提升物理解题的效率.

【关键词】高中物理；数学思维；解题教学

在新课改背景下，落实立德树人的根本任务是高中物理教育教学的重要要求，从高考评价体系的视角来看，试题注重考查学生对物理基础知识与规律的探究以及学生的科学思维能力.本文从典型试题入手，重点探讨利用数学知识解决物理问题的具体方法和教学建议，以期助力高中物理课堂教学.

1 借助数学图象剖析物理问题

以图象方式表征文字陈述和物理公式的物理试题，在各级大型质量测试中经常出现，解决这类物理试题主要从数学函数图象斜率、纵横轴截距、图象交点、极值等角度进行思考，在解决物理问题的过程中不断提升学生分析问题、解决问题、科学推理和综合应用能力，助力学生科学思维能力的提升.

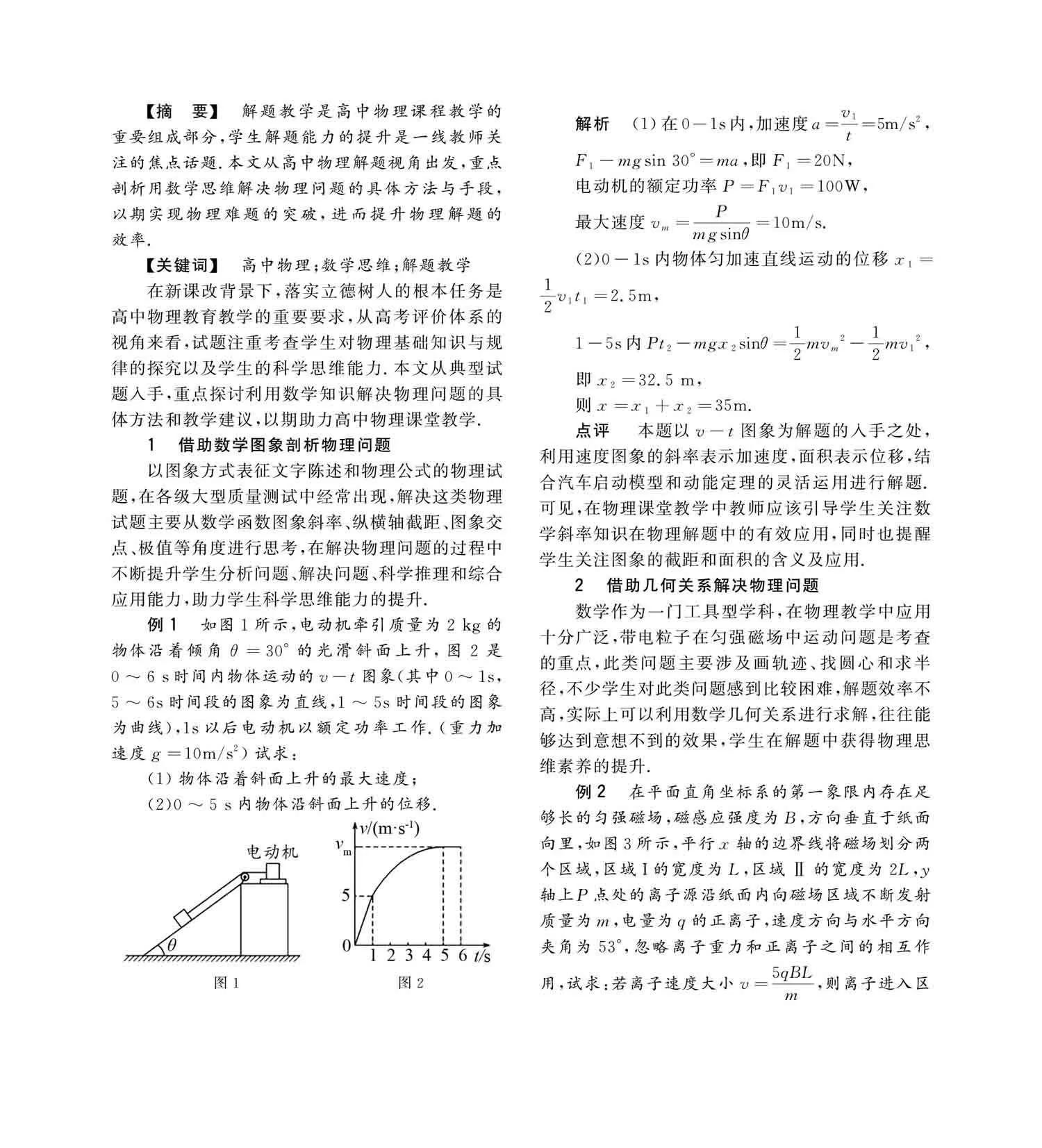
例1 如图1所示，电动机牵引质量为2 kg的物体沿着倾角θ＝30°的光滑斜面上升，图2是0～6 s时间内物体运动的v－t图象（其中0～1s，5～6s时间段的图象为直线，1～5s时间段的图象为曲线），1s以后电动机以额定功率工作.（重力加速度g＝10m/s2）试求：

（1）物体沿着斜面上升的最大速度；

（2）0～5 s内物体沿斜面上升的位移.

解析 （1）在0-1s内，加速度a=v1t=5m/s2，

F1-mgsin 30°=ma，即F1=20N，

电动机的额定功率P=F1v1=100W，

最大速度vm=Pmgsinθ=10m/s.

（2）0-1s内物体匀加速直线运动的位移x1=12v1t1=2.5m，

1-5s内Pt2－mgx2sinθ=12mvm2-12mv12，

即x2=32.5 m，

则x=x1+x2=35m.

点评 本题以v－t图象为解题的入手之处，利用速度图象的斜率表示加速度，面积表示位移，结合汽车启动模型和动能定理的灵活运用进行解题.可见，在物理课堂教学中教师应该引导学生关注数学斜率知识在物理解题中的有效应用，同时也提醒学生关注图象的截距和面积的含义及应用.

2 借助几何关系解决物理问题

数学作为一门工具型学科，在物理教学中应用十分广泛，带电粒子在匀强磁场中运动问题是考查的重点，此类问题主要涉及画轨迹、找圆心和求半径，不少学生对此类问题感到比较困难，解题效率不高，实际上可以利用数学几何关系进行求解，往往能够达到意想不到的效果，学生在解题中获得物理思维素养的提升.

例2 在平面直角坐标系的第一象限内存在足够长的匀强磁场，磁感应强度为B，方向垂直于纸面向里，如图3所示，平行x轴的边界线将磁场划分两个区域，区域I的宽度为L，区域Ⅱ的宽度为2L，y轴上P点处的离子源沿纸面内向磁场区域不断发射质量为m，电量为q的正离子，速度方向与水平方向夹角为53°，忽略离子重力和正离子之间的相互作用，试求：若离子速度大小v=5qBLm，则离子进入区域Ⅱ与边界的夹角θ.

解析 以v=5qBLm进入磁场区域I运动轨迹如图4所示，做匀速圆周运动的半径r=mvqB=5L，根据几何关系可知，离子匀速圆周运动的圆心至区域Ⅱ边界的距离d=rcos53°+L=4L，则cosθ=dr=0.8，即θ=37°.

点评 带电粒子在磁场中的运动问题是高中物理考查的重点和难点，解决此类问题主要是根据题意画轨迹，根据圆周运动特征找圆心，再根据数学几何关系求半径，结合洛伦兹力提供向心力列方程进行求解.此类问题解决的关键是“数学几何知识”求半径的过程，物理教师应该重视引导学生运用数学几何知识求解问题.

3 借助微元思想求解物理问题

物理解题方法的探讨一直是一线教师关注的焦点，解题方法的灵活运用是高效解题的重要保障.微元法是从数学视角对研究对象进行无限截取微小单元，对该微元进行物理分析及规律运用进行解决问题.微元思想方法能够有效处理变量问题，特别是电磁感应中的相关问题.

例3 在水平面内固定一个顶角θ=45°的金属导轨MON，如图5所示，磁感应强度为B的匀强磁场垂直于导轨向下，质量为m的导体棒与ON垂直，在水平外力作用下以恒定速度v0沿导轨MON向右滑动，导轨与导体棒单位长度的电阻均为r，导体棒在滑动过程中始终保持与导轨良好接触；t=0时，导体棒位于顶点O处，在水平外力作用t0时刻后撤去，试求：导体棒移动的最远水平距离.

解析 根据题意，撤去外力后，设任意时刻t导体棒的运动距离为x，速度为v，取很短时间Δt（很短距离Δx）.

如图6所示，在t～t＋Δt内，由动量定理得－BIlΔt＝mΔv，

根据欧姆定律可得

I=ER=Blv2+2lr=Bv2+2r，

则－∑B22+2rlvΔt=∑mΔv，

B22+2rΔs=mv0，

在此过程中扫过面积ΔS=x0+xx－x02=x2－x202，（x0＝v0t0），

可得x=22+2mv0rB2+v0t02.

点评 本题主要涉及电磁感应中的变速运动问题，导体棒撤去外力后做加速度不断减小的减速运动，常规的匀变速运动公式难以处理，对于这类变速问题处理的常见手段是微元法，选取微元Δt、Δv、ΔS，让变量视为衡量处理，再利用微元累积求和实现难点的突破与求解，不断提升学生数学思想方法融合物理解题的应用能力.

4 结语

总而言之，数学思想方法是解决物理问题的一种重要手段，物理教师在教学实践中应该引导学生灵活运用数学知识与规律解决物理问题，让学生实现物理问题向数学问题的转化，达成数学思维在物理解题中有效应用的目标，进而培养学生物理学科的思维素养，促进学生物理学科核心素养的发展.

参考文献：

［1］陶德泉.数学知识与思想方法在高中物理解题中的应用探究［J］.数理化解题研究，2023（22）：130-132.

［2］刘长强.数学定理在高中物理力学解题中的有效应用研究［J］.中学理科园地，2022（03）：65-68.