高中物理绳杆中的运动分解问题探究

【摘要】在高中物理教学中，绳杆中的运动分解问题是一个重要的内容.本文通过对绳杆运动分解问题的探讨，旨在帮助学生更好地理解运动的合成与分解，提高学生解决问题的能力.通过实例分析，展示绳杆运动分解问题在实际问题中的应用.

【关键词】高中物理；绳杆运动；解题技巧

1 引言

绳杆运动分解是基于运动的合成与分解原理.在绳杆运动中，通过将物体的运动分解为沿绳杆方向和垂直于绳杆方向的两个分运动，可以将绳杆运动问题分解为两个独立的分运动问题，分别求解后再进行合成.通过运用运动的合成与分解原理，学生可以将复杂的绳杆运动问题分解为简单的分运动，从而简化问题并求解.

2 绳杆中运动分解问题概述

例1 如图1所示，在小船靠岸模型中，轻绳通过定滑轮连接小船，绳端速度为v，方向水平，当船连接的轻绳与水平面的夹角为α时，求小船的运动速度.

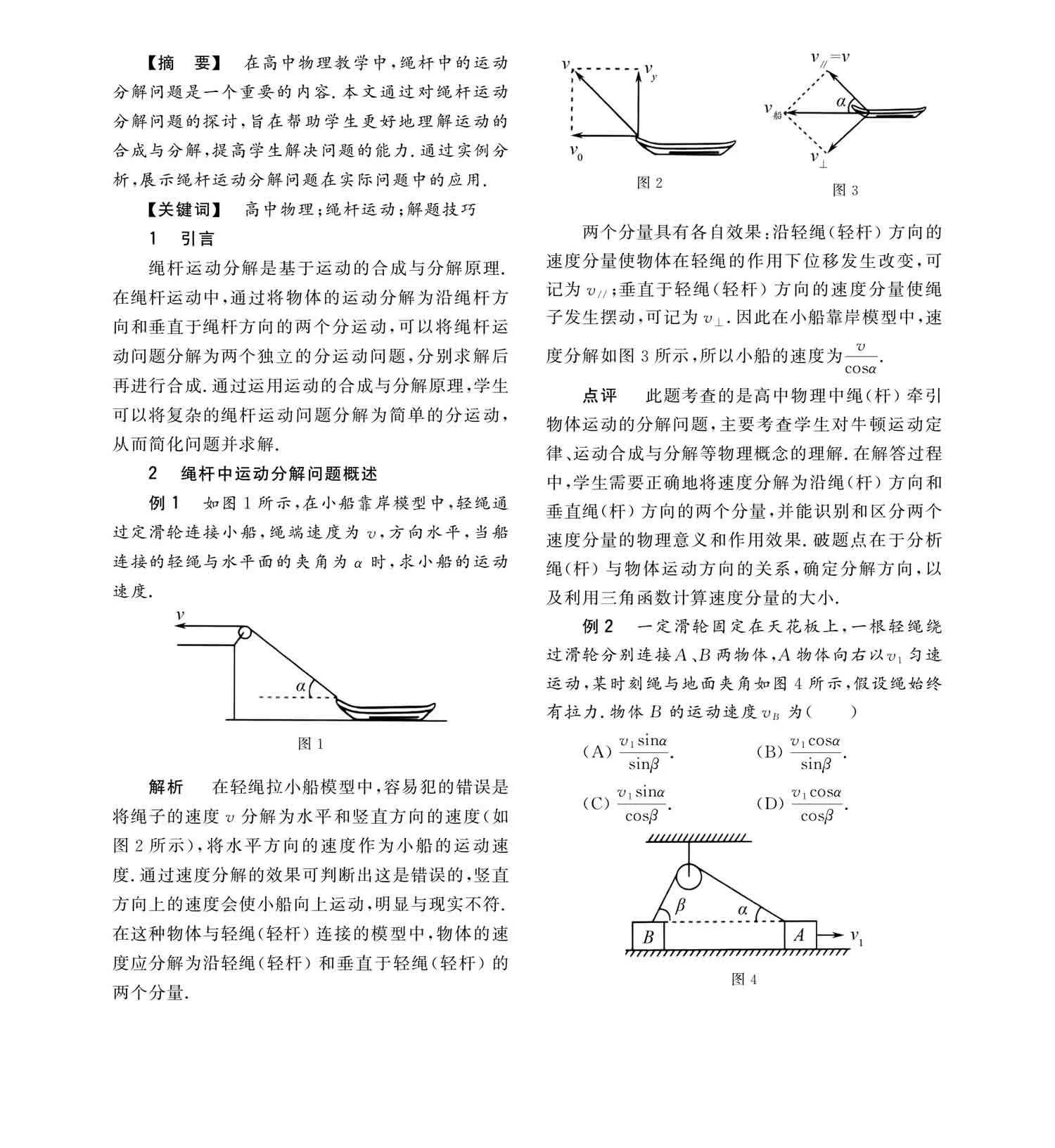
解析 在轻绳拉小船模型中，容易犯的错误是将绳子的速度v分解为水平和竖直方向的速度（如图2所示），将水平方向的速度作为小船的运动速度.通过速度分解的效果可判断出这是错误的，竖直方向上的速度会使小船向上运动，明显与现实不符.在这种物体与轻绳（轻杆）连接的模型中，物体的速度应分解为沿轻绳（轻杆）和垂直于轻绳（轻杆）的两个分量.

两个分量具有各自效果：沿轻绳（轻杆）方向的速度分量使物体在轻绳的作用下位移发生改变，可记为v//；垂直于轻绳（轻杆）方向的速度分量使绳子发生摆动，可记为v⊥.因此在小船靠岸模型中，速度分解如图3所示，所以小船的速度为vcosα.

点评 此题考查的是高中物理中绳（杆）牵引物体运动的分解问题，主要考查学生对牛顿运动定律、运动合成与分解等物理概念的理解．在解答过程中，学生需要正确地将速度分解为沿绳（杆）方向和垂直绳（杆）方向的两个分量，并能识别和区分两个速度分量的物理意义和作用效果．破题点在于分析绳（杆）与物体运动方向的关系，确定分解方向，以及利用三角函数计算速度分量的大小．

例2 一定滑轮固定在天花板上，一根轻绳绕过滑轮分别连接A、B两物体，A物体向右以v1匀速运动，某时刻绳与地面夹角如图4所示，假设绳始终有拉力.物体B的运动速度vB为（ ）

（A）v1sinαsinβ. （B）v1cosαsinβ.

（C）v1sinαcosβ. （D）v1cosαcosβ.

解析 如图5、图6所示，将A和B的速度分解为沿轻绳和垂直于轻绳方向，因为轻绳长度不发生变化，故沿着轻绳方向速度相等，所以vBcosβ=v1cosα，解得vB=v1cosαcosβ，故（D）正确.

点评 本题考查学会对物体进行运动的分解，涉及平行四边形定则与三角函数知识，同时本题的突破口是沿着绳子的方向速度大小相等．在解答过程中，学生仍然需要正确地将速度分解为沿绳方向和垂直绳方向的两个分量，并利用滑轮系统中绳子各点速度相等的特性，不能直接将绳子的速度等同于物体的速度，特别是在有角度的情况下，要注意区分沿绳方向和垂直绳方向的速度分量对物体运动的不同影响，并在实际问题中考虑重力、摩擦力等其他可能影响物体运动的因素．

例3 光滑地面和竖直墙面呈垂直状态，小明将长直轻杆AB靠在墙面，某时刻松手，轻杆开始滑动，当轻杆滑动至如图7所示状态时，轻杆与墙面夹角为θ，A端速度大小为v1，B端速度大小为v2，则v1，v2的关系是（ ）

（A）v1=v2. （B）v1=v2cosθ.

（C）v1=v2tanθ. （D）v1=v2sinθ.

解析 如图8所示，将A端和B端速度分解为沿轻杆和垂直于轻杆的速度分量，因为沿杆方向速度相等，所以v1cosθ=v2sinθ，解得v1=v2tanθ，故（C）正确.

点评 本题虽不同于前两例，但解题本质依然是速度的正确分解，解决本题的关键是将A、B两点的速度分解为沿杆子方向和垂直于杆的方向，以及知道沿杆方向上的两个分速度大小相等．

3 结语

本文通过对绳杆运动分解问题的探讨，介绍了绳杆运动分解的原理和技巧解法的应用.通过实例分析，展示了绳杆运动分解问题在实际问题中的应用.掌握绳杆运动分解的方法对于理解和解决高中物理中的相关问题具有重要意义.

参考文献：

［1］江明隆.高中物理运动体系分解的经验方法［J］.当代旅游（高尔夫旅行），2018（07）：181.

［2］郑南轩.关于运动分解的一些要点阐述［J］.中外企业家，2018（15）：106.

［3］李昱龙.高中物理中的运动分解法［J］.农家参谋，2017（19）：87.