例谈空间直角坐标系的构建

引入空间向量坐标运算，使立体几何问题避免了传统方法中烦琐的分析运算过程，只需建立空间直角坐标系便可轻松求解。要建立恰当的坐标系是利用向量解题的第一步，也是关键步骤之一。下面谈谈建系的原则及常见模型，供同学们参考。

一、建立直角坐标系的原则

1.z 轴的选取往往是比较容易的，依据线面垂直的判定定理，即z 轴要与坐标平面xOy 垂直，在几何体中也很直观，坐标原点即为z 轴与底面的交点。

2.x 轴，y 轴的选取对坐标是否易于写出非常关键，下面几个原则值得参考。

（1）尽可能地让底面上更多的点位于x轴，y 轴上;

（2）因为x 轴，y 轴要相互垂直，所以要利用好底面中的垂直条件;

（3）要利用好对称关系，寻找底面上的点是否存在轴对称。

3.同一个几何体可以有不同的建系方法，其坐标也会对应不同，但是通过坐标运算所得到的结论（位置关系，角）是一致的。

二、常见模型

1.墙角模型：已知条件中有过一点且两两相互垂直的三条直线，就是墙角模型。

以该点为原点，分别以两两垂直的三条直线为x 轴，y 轴，z 轴，建立空间直角坐标系;当条件不明显时，要先证明过一点的三条直线两两垂直（即一个线面垂直+底面内两条直线垂直），然后建系。

2.垂面模型：已知条件中有一条直线垂直于一个平面，此情形包括垂足在平面图形的顶点处、垂足在平面图形的边上（多为中点）和垂足在平面图形内部三种情况。

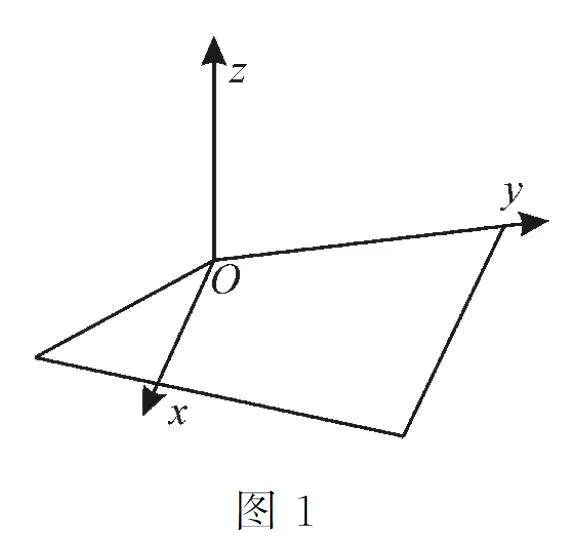
第一种建系方法以垂足为坐标原点，垂线的向上方向为z 轴的正方向，平面图形的一边为x 轴或y 轴，在平面图形中，过原点作x 轴或y轴的垂线，对应为y 轴或x 轴（其中很多题目是连接垂足与平面图形的另一顶点），建立空间直角坐标系，如图1。

第二种建系方法以垂足为坐标原点，垂线的向上方向为z 轴的正方向，垂足所在的一边为x轴或y 轴，在平面图形中，过原点作x 轴或y 轴的垂线，对应为y 轴或x 轴（其中很多题目是连接垂足与平面图形的另一顶点），建立空间直角坐标系，如图2。

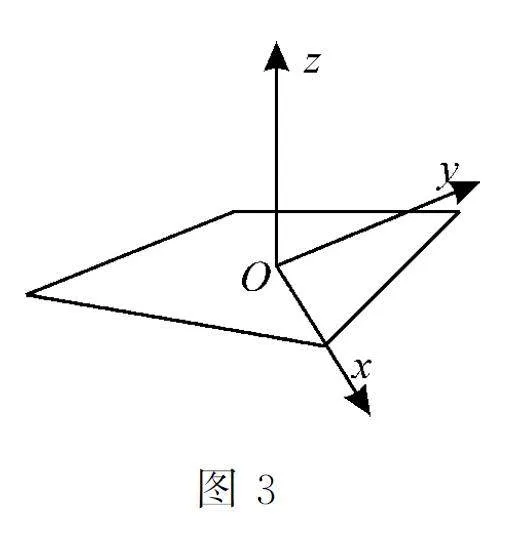
第三种建系方法以垂足为坐标原点，垂线的向上方向为z 轴的正方向，连接垂足与平面图形的一顶点所在直线为x 轴或y 轴，在平面图形中，过原点作x 轴或y 轴的垂线，对应为y 轴或x 轴（其中很多题目是连接垂足与平面图形的另一顶点），建立空间直角坐标系，如图3。

三、常考题型

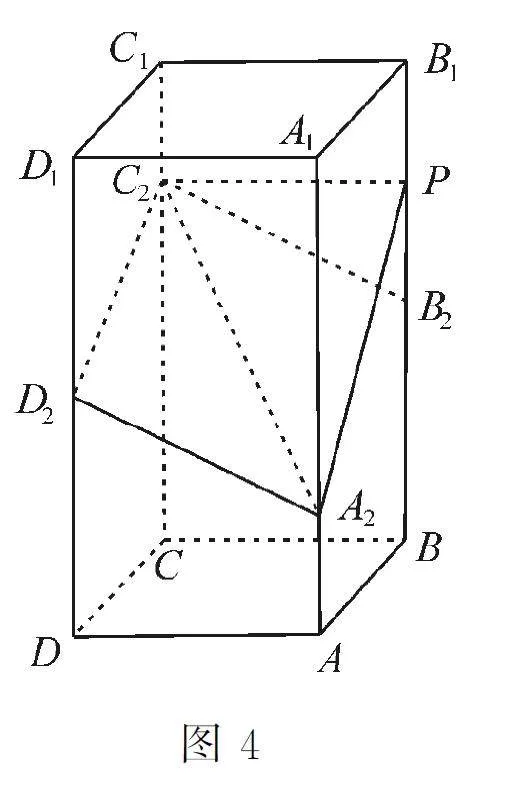
例1 （2023年全国高考新课标Ⅰ卷）如图4，在正四棱柱ABCDA1B1C1D1中，AB = 2，AA1=4。点A2，B2，C2，D2分别在棱AA1，BB1，CC1，DD1 上，AA2 =1，BB2 =DD2=2，CC2=3。

（1）证明：B2C2∥A2D2;

（2）点P 在棱BB1 上，当二面角P-A2C2-D2 为150°时，求B2P 的值。