基于CFD模拟风帆对船舶推力系数的探究



摘要:自然环境恶化,石油资源枯竭是当今世界面临的两个严峻问题。风帆助航技术因为具有节能环保的特性,符合可持续发展理念,本文将采用CFD数值模拟方法,分别对船舶安装风帆的流场进行数值模拟,研究风帆在对0°~90°攻角时风帆的升阻力系数以及推力系数的影响。发现25°攻角时,风帆的升力系数达到最大,当攻角大于50°时,阻力系数大于升力系数;不同的风向角下出现的最佳攻角是不同的,同样最佳推力系数也是不同的,可以在不同的风向角下改变攻角来提高推力系数。
关键词:风帆助航;风向角;推力系数
中图分类号:U661.43文献标识码:A
0 引言
在全球物流体系中,以船舶为载体的海上运输是最重要的货物运输途径之一。据统计,当今世界上有90%以上的货物都需要靠船舶运输。但与此同时,航运业所消耗的石油资源以及向大气中排放的污染物的数量也是惊人的,比如SOx、NOx和CO的排放量分别占全球排放总量的10%、25%和2.7%[1]。能源危机将成为人类发展无法逾越的鸿沟,世界各国各地区也相继制定了航运业大气污染的防治措施,对于清洁能源的开发与研究也在同步进行。在众多可再生能源中,风能以其独特的优势,获得了广泛的应用。风能是大气的流动而引起的动能,它的实质是太阳能,具有无污染、可以再生、分布广泛、储量较大等诸多优点[2]。海上风能密度相对较高,储量丰富,比较容易开发利用,若能借助风能辅助船舶航行,达到节省船舶主机功率或提高船舶航速的目的,将会在大幅减少船舶的燃料消耗,减小船舶运行对环境的危害。船舶安装风帆是为了利用风能获得推力,减小主机的燃油消耗。
国外对风帆助航的研究起步较早,德国、美国、日本等国均对风帆助航进行了大量的研究。德国在上1960年便着手研究风帆助航船舶,设计了风帆助航船“DYNA”号;美国在70年代曾创建了风帆委员会,进行一系列关于船舶风帆的研究,并在一艘名为“大西洋”号的商船上安装一面三角帆,可以节省20%的油耗;法国船东曾出资打造了一艘以抽气式涡轮帆为辅助动力的探险船“Alcyone号”,可节省大约35%的燃料[3];东京大学联合日本的航运公司共同启动了“风之挑战者项目”(Wind Challenger Project)[4]。目的是利用海上的风能推动大型货船航行,设计了在一艘安装9面大型硬帆的18万吨散货船,在12m/s的横向风下,该船无需主机功率便可以达到14节的航速[5]。80年代,我国对风帆助航的研究方才起步,上海交大、武汉水运工程学院等高校针对风帆助航的可行性,风帆的流体动力学特性,风帆的自动控制等进行了大量研究。上海交通大学张仁颐提出了基于动力增益的估算方法论证了风帆助航船舶的经济可行性,计算得到船上安装风帆后的可以节省能耗10%~15%。
1 模型设置
1.1目标船型
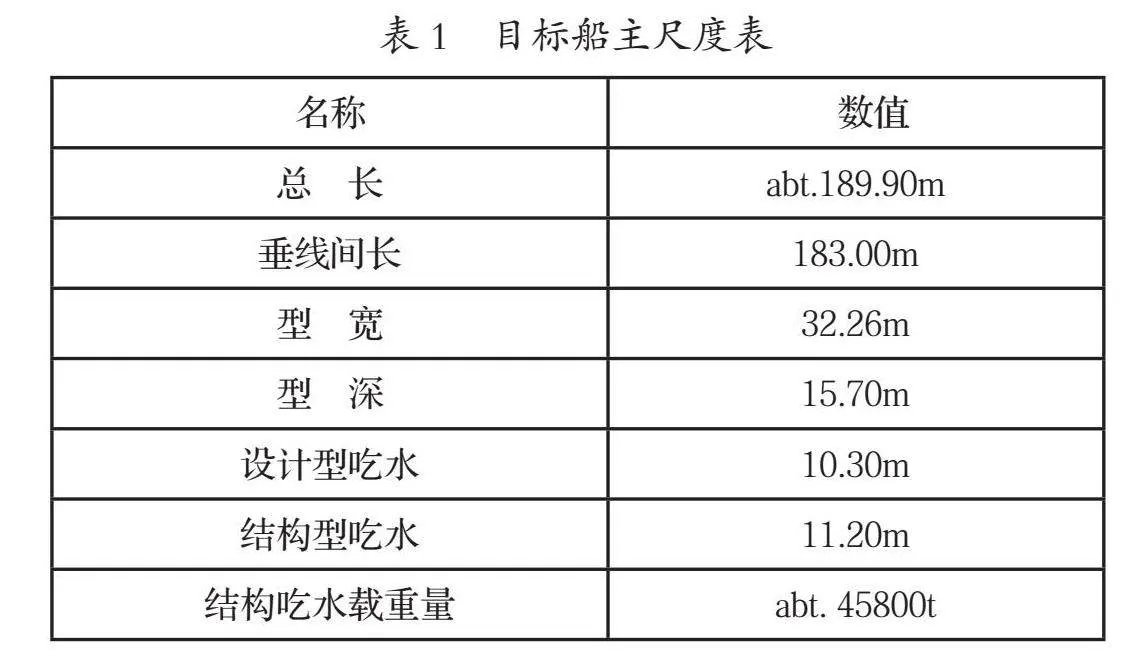
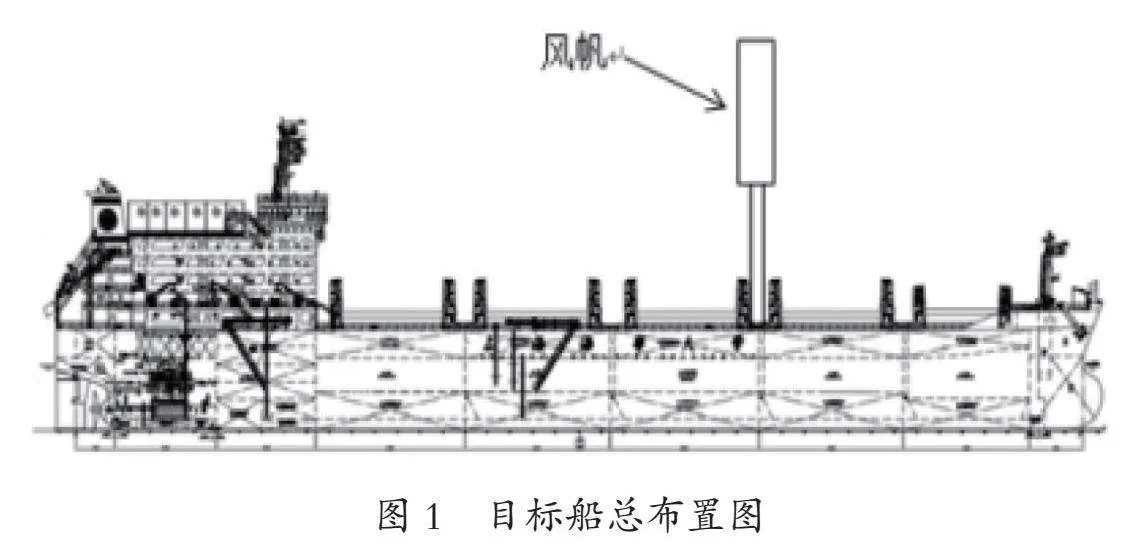
本文所选取的目标船为一艘无限航区的48000t远洋散货船,该船的主尺度见表1,总布置如图1所示。该船型体宽大,船舶重心高度低,上层建筑少,甲板布置宽敞,适合安装风帆。但是在安装风帆时,桅杆高度不能低于驾驶甲板的高度,否则会阻挡视线,为船驾驶造成潜在的危险。
1.2目标帆型的几何特性
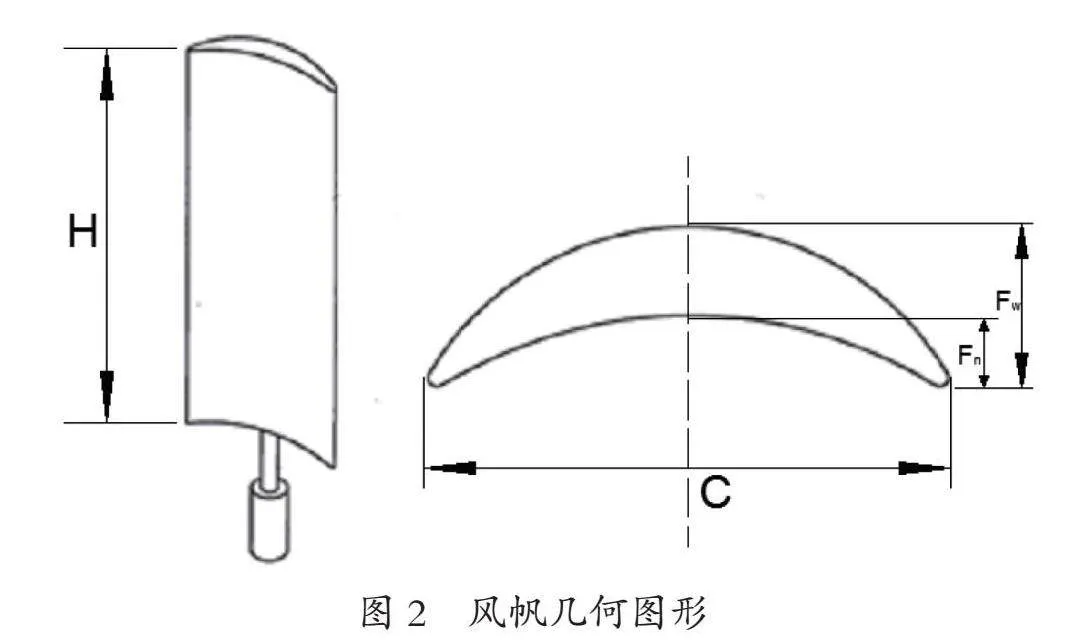
椭圆弧形帆的几何特征如图2所示,其中风帆的展高用H表示,弦长用C表示,外拱高度用F表示,内拱高度F表示,F/C为拱度比,H/C为展弦比。本文所使用的椭圆弧形帆的内拱拱度比F/C=0.16;外供拱度比F/C=0.28;展弦比H/C=0.7。桅杆高度21m,风帆展高为H为26m,弦长C为18m。
2 风帆空气动力学数值模拟
2.1风帆的空气动力学系数
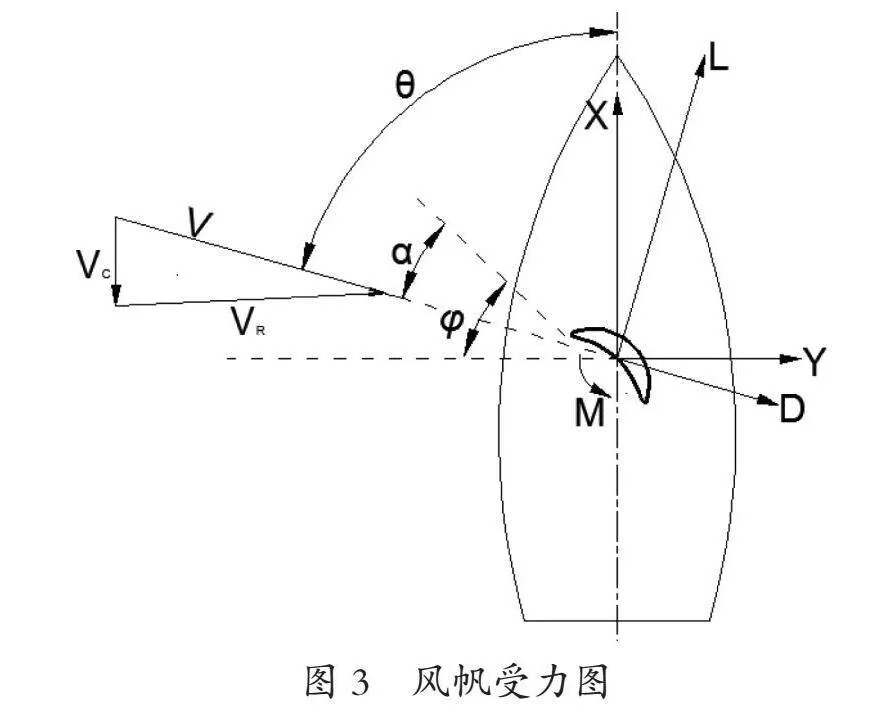
如图3,表观风速V为真实风速VR和船速引起的风速Vc的矢量和,风向角![]() 为表观风速与船舶航向的夹角,帆位角
为表观风速与船舶航向的夹角,帆位角![]() 为风帆弦线与船体中横剖面的夹角。当表观风以速度V和风向角
为风帆弦线与船体中横剖面的夹角。当表观风以速度V和风向角![]() 流向风帆时,假设此时帆位角为
流向风帆时,假设此时帆位角为![]() ,那么表观风速V和风帆弦线之间存在一个夹角
,那么表观风速V和风帆弦线之间存在一个夹角![]() ,称夹角
,称夹角![]() 称为几何攻角。则风帆的此时受到的力可分解为平行与表观风速V的阻力D,垂直于表观风速V的升力L以及对桅杆的力矩M[6]。若将升力L和阻力D表示成无因次系数,则有:
称为几何攻角。则风帆的此时受到的力可分解为平行与表观风速V的阻力D,垂直于表观风速V的升力L以及对桅杆的力矩M[6]。若将升力L和阻力D表示成无因次系数,则有:
升力系数:![]()
阻力系数:![]()
如果将升力L和阻力D分解为船前进方向的力X和垂直于船前进方向的横向力Y,那么得:
风帆对船舶的推力:![]()
风帆对船舶的横向力:![]()
若使用无因次系数来表示,则有:
推力系数:![]()
2.2湍流模型
本文基于Fluent进行帆船的数值模拟,在Fluent中对空气进行流动模拟仿真,并在其中选择湍流模型,大涡模拟(LES)方法的理念是对湍流中大尺度涡使用瞬时的N-S方程计算,但是对于湍流中存在的小尺度涡则使用简化的近似模型来处理。工程实践中较多运用的是RANS方法[7]。RANS方法不需要直接求解瞬时的N-S方程,只需要求解时均化的Reynolds方程,如若把湍流运动看作是时间平均流动与瞬时脉动流动相叠加而成的运动,那么场变量瞬时值![]() 可以表示为时均值
可以表示为时均值![]() 和脉动值
和脉动值![]() 的相加之和,即:
的相加之和,即:![]() ,可以得到时均形式的连续方程:
,可以得到时均形式的连续方程:![]() 和时均形式的Navier-Stokes方程(Reynolds方程、RANS方程):
和时均形式的Navier-Stokes方程(Reynolds方程、RANS方程):![]()
另外,工程实际中,还要用到涡粘模型,涡粘模型通过引入湍流粘度,将湍流应力转换湍流粘度的函数,本文所计算的风帆流动的最大雷诺数在107量级,属于高雷诺数流动,数值模拟时采用Realizable![]() 模型,并采用标准壁面函数处理近壁面区域的流动[8]。
模型,并采用标准壁面函数处理近壁面区域的流动[8]。
3 风帆数值模拟分析
3.1风帆数值模拟分析
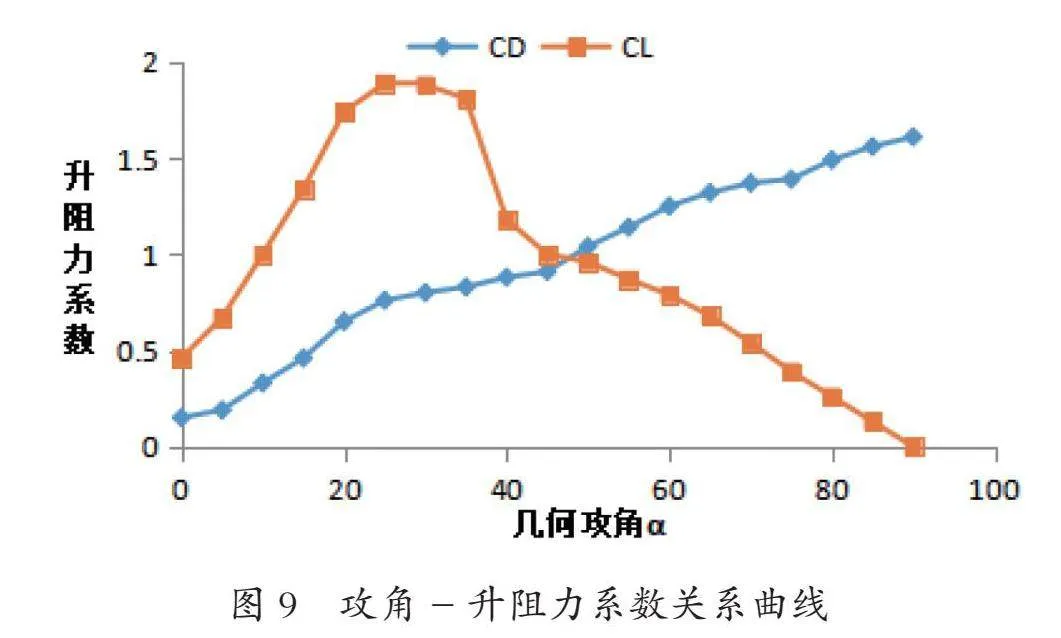
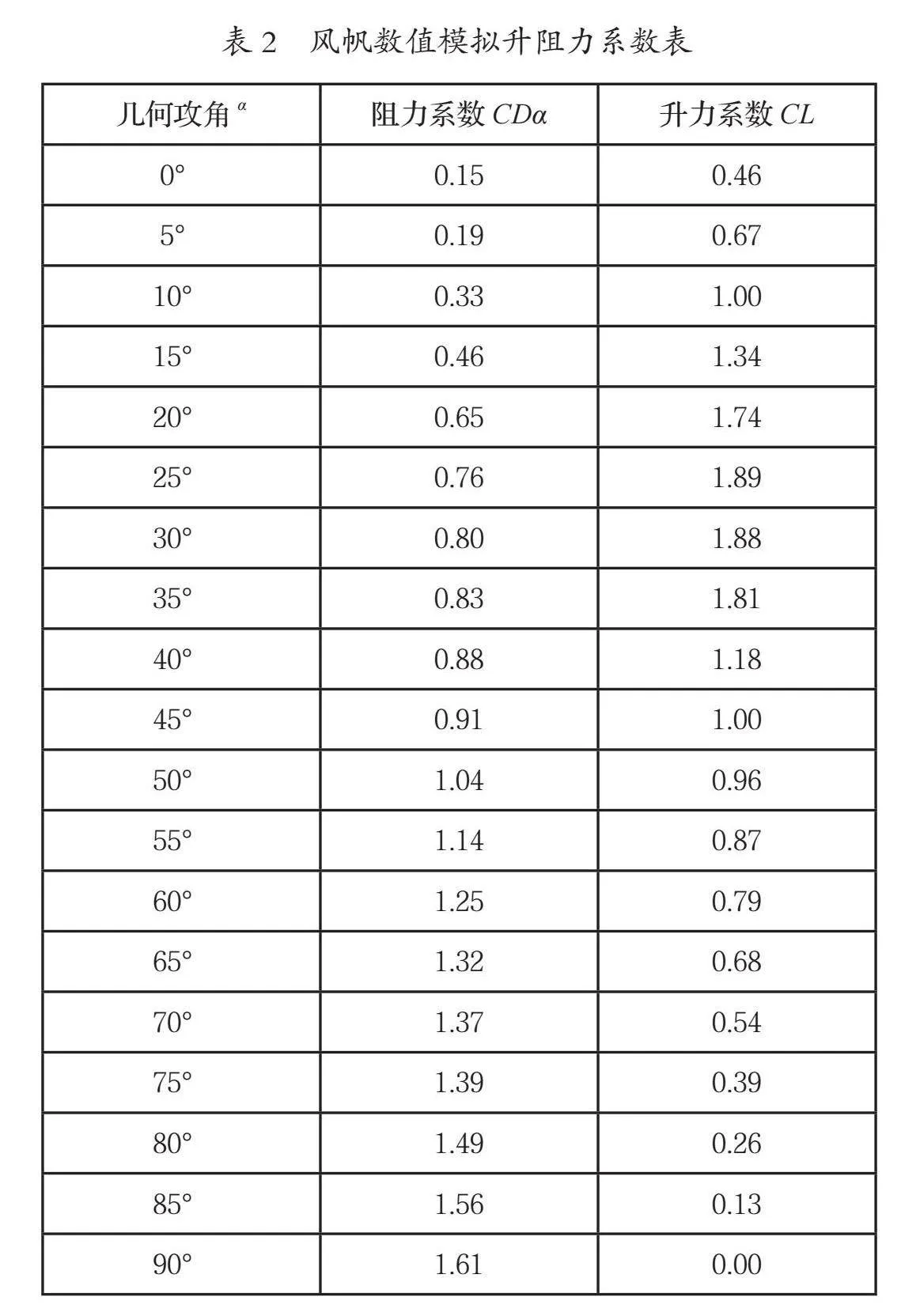
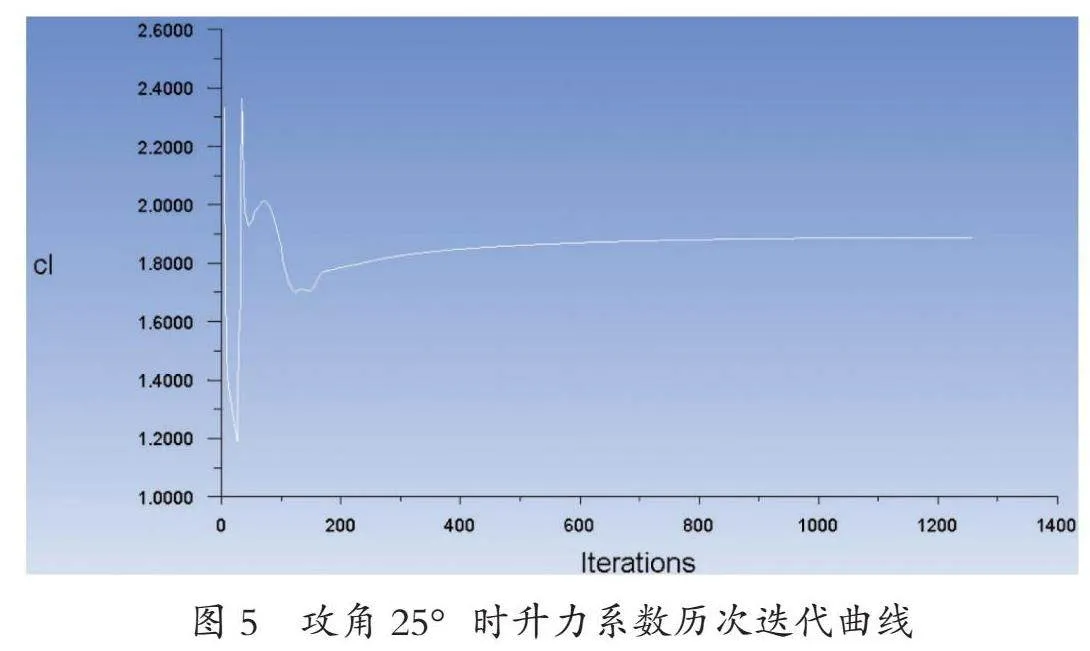
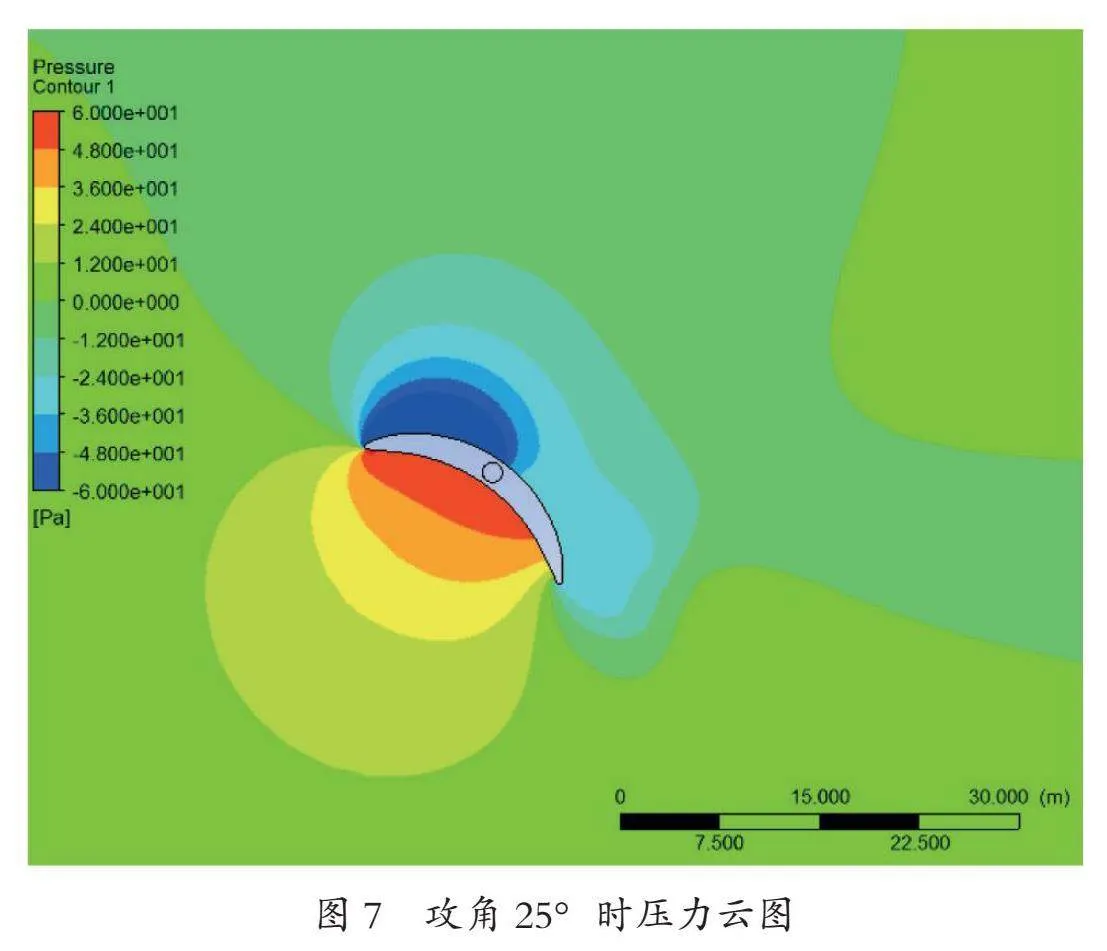
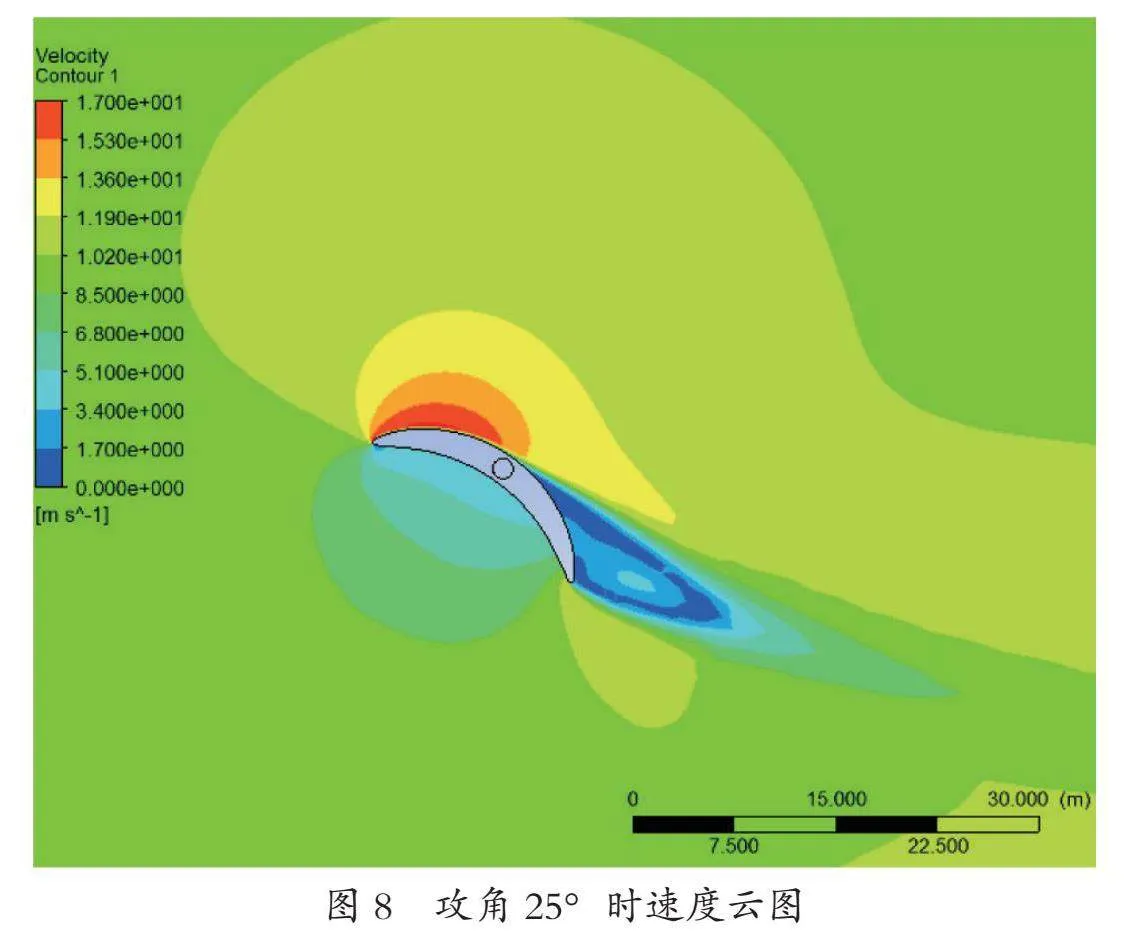
使用Fluent对0°~90°攻角时风帆的升阻力系数进行计算,每隔5°计算一次。攻角为25°时,升力系数、阻力系数和残差历次迭代曲线如图4~6所示,图7和8分别是攻角25°时的流场的压力和速度云图。计算结果如表2所示。
由表2和图9可以看出:
(1)当风帆攻角从0°增加到90°时,风帆在空气流动方向的投影面积逐渐增大,风帆的阻力系数也呈现出逐渐升高的趋势;
(2)当风帆攻角从0°增加到90°时,风帆的升力系数呈现出先升高后降低的趋势。当攻角为25°左右时,风帆的获得最大升力系数,此时升力系数远大于阻力系数;
(3)当攻角超过50°以后,风帆的阻力系数大于升力系数。
4 结论与展望
由仿真模拟可知:由于风帆在来流方向的投影面积逐渐增大,风帆的阻力系数也呈现出逐渐升高的趋势;当攻角从0°增加到90°时,风帆的升力系数呈现出先升高后降低,当攻角为25°左右时风帆的升力系数达到最大;风帆的阻力系数呈现出逐渐升高的趋势,当攻角大于50°时,风帆的阻力系数超过升力系数;不同的风向角都有对应的最佳帆位角、几何攻角和最大推力系数,故在船舶航行中可以调整风向角来提高推力。
对风帆以进行数值模拟时,均未考虑船体的影响,未考虑自然风下速度梯度的影响。今后的研究中可以使用UDF函数对入口边界条件进行设置以模拟自然风场,并对船体-风帆进行综合建模,综合考虑船体以及自然风场的影响。
参考文献
[1]郑悦红, 郭汉丁,吴思材,陈思敏.我国能源现状分析及其发展策略[J].城市,2018(01):35-42.
[2]王分良. EEDI时代的船舶减排[J].中国船检,2009(08):62-65.
[3]孟维明,赵俊豪,黄连忠.风帆助航节能船的应用前景[J].船舶,2009,20(04):1-3.
[4]Ouchi, Kazuyuki, et al. “Wind Challenger” the next Generation Hybrid Sailing Vessel[C]. The third International Symposium on Marine Propulsors, Launceston, Tasmania, Australia. 2013.
[5]Fujiwara T, Hirata K, Ueno M, et al. On Aerodynamic Characteristics of a Hybrid-Sail with Square Soft Sail[J]. Proceedings of the International Offshore and Polar Engineering Conference, 2003: p2576-2583
[6]胡以怀,李松岳,曾向明.一种翼型风帆的空气动力特性计算[J].造船技术,2011(01):16-19.
[7]林虹兆. 圆弧型风帆的气动优化及双帆干扰研究[D].大连海事大学,2016.
[8]胡以怀,李妍嫣,唐娟娟.风帆阵列气动干扰特性数值分析[J].造船技术,2017(01):6-11.
作者简介:何永明(1994年5月-),男,硕士研究生,船舶管理。
地址:上海市宝山区淞浦路181号
邮编:200940
电话:18221355175
E:173621594@qq.com

