高校教师绩效多准则定量评价机制创新与分析研究

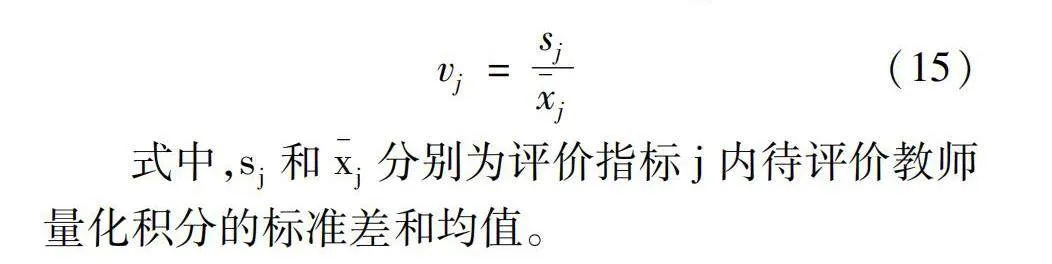
摘 要：采用熵权TOPSIS方法建立了包含人才培养、科学研究、社会服务等相关指标的高校教师多准则绩效评价模型，对比了原积分排名与TOPSIS模型、熵权TOPSIS模型的绩效评价结果，讨论了评价指标变化及样本变化对指标间权重分布及评价结果的影响。发现熵权TOPSIS模型中内部差异化大的指标具有高权重，并使在内部差异化大的指标中表现突出的教师排名提升，评价结果明显区别于积分排序。评价指标的增减不影响原评价指标的权重排序，但指标权重增大或者减小的量与其原来权重的排序成正比。评价对象数量的增减将改变评价指标权重，并对评价结果排序产生影响。结果表明：通过建立分类考核与评价机制，平衡导向性和多元性的指标体系，选取科学合理的业绩量化标准，熵权TOPSIS方法可以客观、综合地评价教师取得的成果。

关键词：高校；绩效评价；多准则；熵权；TOPSIS

中图分类号：G 647

文献标识码：A

文章编号：1672-7312（2024）05-0477-12

Innovation and Analysis of Multi-criteria Quantitative Evaluation Mechanism for College Teachers’ Performance

YANG Fuqiang

（College of Science，Xi’an University of Science & Technology，Xi’an 710054，China）

Abstract：A multi-criteria performance evaluation model for college teachers，which include talents training，scientific research，social service and other related evaluation indexes，was established by adopting entropy weight TOPSIS method.The teachers’ performance under the original score ranking method，TOPSIS model and entropy-weighted TOPSIS model was evaluated，the effects of evaluation index and sample change on the evaluation index weights and the evaluation results were also discussed.It is found that the evaluation index with large internal differences have high weights in the entropy-weighted TOPSIS model，which will improve the ranking of teachers with outstanding performance in these indexes，and lead to the obviously different evaluation results with score ranking.The adding or dropping one of the evaluation indexes does not affect the weight ranking of the original evaluation indexes，but the increase or decrease of the indexes’ weights are proportional to the original weight ranking.The adding or dropping of the evaluation objects will change the weight of the evaluation indexes and influence the evaluation results.The results indicate that the entropy-weighted TOPSIS method can evaluate the teachers’ achievements objectively and comprehensively by combining a classification assessment and evaluation mechanism，an orientation and pluralism balanced index system，and a scientific and reasonable quantitative standards.

Key words：college；performance evaluation；multi-criteria；entropy weight；TOPSIS

0 引言

科学、高效、规范的教师绩效考核机制能准确反映教师的工作成效，调动教师工作的积极性^[1]。高校具有人才培养、科学研究和社会服务等功能定位，因此各学校和学院在制定绩效考核时，也围绕这些功能定位建立考核体系并制定考核指标进行实践^[2-4]。教师的考核评价指标与学校的工作重心和发展目标相契合，对学校的发展具有十分重要的作用，因此建立的评价考核体系必须能够综合衡量具有不同特点的教师业绩^[5]。

国内外诸多学者对教师绩效评价的原则进行了深入探讨，以使高校教师绩效评价遵循大学的使命和职能，并回归教育本质。周玲等认为应当结合人才培养的核心目标，以“教书育人”为本位，对教师在教研结合、产教融合、学科交叉与融合等方面的成果进行综合评价。周双喜等^[6]提出高校教师绩效评价应当在均衡思维下进行，遵循战略性、发展性、系统性和多元化原则，把握好总结性评价和发展性评价、学生评教和同行评价、重点角色和一般角色、定量评价和定性评价之间的“度”，建立契合教师特点和发展性目地的均衡多主体利益的绩效评价体系。郑丹^[7]从善治的角度提出高校教师的绩效评价应当具有合法性、透明性和高效率等特点，并从多元主体共同参、效率增益导向及反馈和教师可持续等方面给出了绩效评价优化策略。苏强等^[8]认为提升评价标准的适切性、加强评价过程的协商性、增进评价结果的信效度等，是教师评价制度所面临的根本性问题，应建立“专业发展为主，绩效问责为辅”的评价体系、专业化双向对话平台及综合评价方法，保障评价活动的科学、合理与公正。杨帆^[9]从区域特色研究型高校创建的视角，以教师的社会影响力、学生发展质量、教师的专业素养以及教师的学习与成长等四个维度作为评价指标，构建教学科研岗教师绩效评价体系。通过对高校绩效评价原则的讨论可以得出，建立科学的考核指标体系是教师绩效评价的关键。

针对高校教师的业绩考核指标体系的研究有很多，并从不同的角度构建了评价体系。张宁^[10]从素质、科研、教学及其他工作方面构建教师绩效评价维度，通过建立模糊评判集，应用层次分析法对高校教师的绩效进行定性分析。袁耀东等^[11]探讨了以育人为导向的多维度绩效评价路径，提出构建多元化、全面性的评价体系，多维度体现教师能力，使教师获得职业认同感，激发教师自我提升源动力。刘亚兰^[12]将教师绩效体系分成了任务绩效和关系绩效两部分，其中教师在教学工作、科研工作、社会服务中承担的工作业绩纳入任务绩效，采用定量评价；将教师自身发展、素质提升及对学校发展支持等作为关系绩效进行定量和定性评价。黄英婉等^[13]除了在指标体系中包含教学和科研工作外，将教师的教龄、学历、职称等作为自然情况指标，将教师日常工作的责任心和道德感作为部门测评指标纳入指标体系；同时将教师分为教学研究型、教学型、研究型三种类型，在使用层次分析法进行绩效考评时给予不同的权重。针对为谁考核、考核什么、如何考核及如何应用等问题，周双喜等^[14]从多主体共赢、多学术共生、多层次衔接、多步骤贯通、多数据整合及多目地搭配等六个方面给出建议，构建高校教师绩效评价体系。在这些高校教师绩效评价中，研究者均提出构建多维度和多层次的多元评价体系，通过多准则决策综合评价教师在各个领域取得的业绩成果，因而采用有效的多准则评价方法是确保教师绩效评价公正实施的先决条件。

多准则决策（MCDM）是一种综合考虑问题不同定性和定量属性，通过为各个属性给出不同权重，综合选择最优方案或对方案排序的决策方法^[15-16]，许多学者将该方法应用于教师绩效评价中。陈秋涵在构建的“三全育人”绩效评价体系中运用层次分析法（AHP）进行绩效评价^[17]。由于AHP方法会因为对评价指标的主观性赋权造成评价结果不能真实反映客观情况，傅艳梅^[18]借助熵权法以客观数据为依据计算权重的特点，综合运用熵权法和层次分析法确定绩效考核各指标的权重。为了克服熵权法在权重中不考虑指标间重复性的弊端，杨妍等^[19]引入CRITIC法解决各指标之间的冲突性，并采用AHP和CRITIC主客观相结合的方式对指标进行赋权。鲁明浩^[20]利用隶属度函数建立各指标的综合评价矩阵，以CRITIC权重法确定各指标的权重系数，对评价等级进行赋分，通过计算模糊综合评价值对教师进行绩效评价。郭涛等^[21]通过在多准则决策分析模型中引入逻辑斯蒂曲线改进S型函数，对高校教师科研绩效进行评价，并构建模型对不同学科之间的教学、科研、社会服务等学术活动进行综合评价。付沙等^[22]将粗糙集（RS）理论和条件信息熵引入高校教师评价中，建立基于粗糙集条件信息熵的综合评价智能模型，最大程度呈现专家的经验、知识对指标重要性的倾向。刘叶等^[23]采用粗糙集理论，将连续型指标数据进行离散化处理后对指标体系进行约简，从而降低模型复杂度。然后依托支持向量机（SVM）的模式识别进行教师绩效考评。以上这些模型在消除教师多准则考核定性评价和定量评价缺点等方面，提供了很好的思路和尝试。

高校教师的绩效评价涉及教学、科研、社会服务等多个维度，且涉及大量评价对象和指标，建立的模型具有客观、便捷地处理复杂数据的特点。TOPSIS模型是一种针对给定的待评估对象，构造出一个理想最优解和最劣解，通过计算待评估对象与理想最优解和最劣解的综合距离，精确地反映各评价对象之间的差距，判断待评估对象的优劣和排序的多目标决策方法。该模型具有流程步骤恒定且与评价指标数量不受限制，计算过程简单且可编程，能同时给出最优和最差的方案等优点^[24-25]。与AHP和ELECTRE等其他技术相比，这些优点使TOPSIS成为主要的MCDM技术^[26]。此外，该方法直接根据评估矩阵和权重中的数据比较每个备选方案^[27]，根据ZANAKIS等^[28]的仿真比较，TOPSIS在该类别的8种方法中排名反转最少。熵权法通过计算各指标的信息熵确定权重，能够客观反映各指标的变异性，避免主观赋权的偏差，提高评价结果的公正性。因此，研究拟在西安科技大学××学院现有教师业绩评价体系基础上，引入熵权法对TOPSIS模型中的指标权重进行修正，克服单纯TOPSIS模型指标同权的问题^[29-30]，建立多维度、多指标、多对象且具有客观公正及操作便捷特点的教师绩效多准则评价模型。通过与现有评价体系比较，分析熵权TOPSIS模型对考核结果的影响及其决定因素，为教师业绩评价改进提供建议。

1 教师多准则绩效计算模型评价

1.1 TOPSIS模型

TOPSIS模型包含6个计算过程。

1）构造决策矩阵。假设评价体系包含有m个待评价对象，n个评价指标，则决策矩阵为

式中，x为第i个待评价对象的第n个评价指标值。

2）归一化决策矩阵R。采用式（2）计算得到归一化的决策矩阵R=（r）

3）计算加权归一化决策矩阵V

V=（v）（3）

式中，v由第j个指标的权重w与式（2）计算得到的r计算得到

v=wr（4）

在TOPSIS中，各指标的权重v相同，因此有v=r。

4）确定最优目标A⁺和最劣目标A^－

5）计算各评价对象与最优、最劣目标的距离

6）计算所有被评价对象与最优目标值的贴近度C及其归一化值C^*

最后根据C的大小进行排序，数值越大表示评价对象越接近最优值。

1.2 熵权TOPSIS模型

为了避免TOPSIS模型中各指标权重w相同的问题，采用熵权法对TOPSIS模型进行修正。熵权法通过评价指标信息熵的大小判断指标变异性的大小并确定权重。较小的信息熵表明该指标的变异程度大，其包含的信息越多，在综合评价中所起的作用和对应权重越大；反之表明该指标的作用较小，对应权重小。熵权法通过以下5个步骤计算权重。

1）构造决策矩阵。该矩阵与式（1）得到的矩阵相同

2）归一化决策矩阵。由于评价指标中的数据在量纲上存在差异，采用式（9）计算得到标准化决策矩阵P=（p）

3）计算每个评价指标的信息熵。对于第j个评价指标，其信息熵为

4）计算信息效用值

d=1－E，∀（11）

5）计算熵权。第j个指标的权重计算为

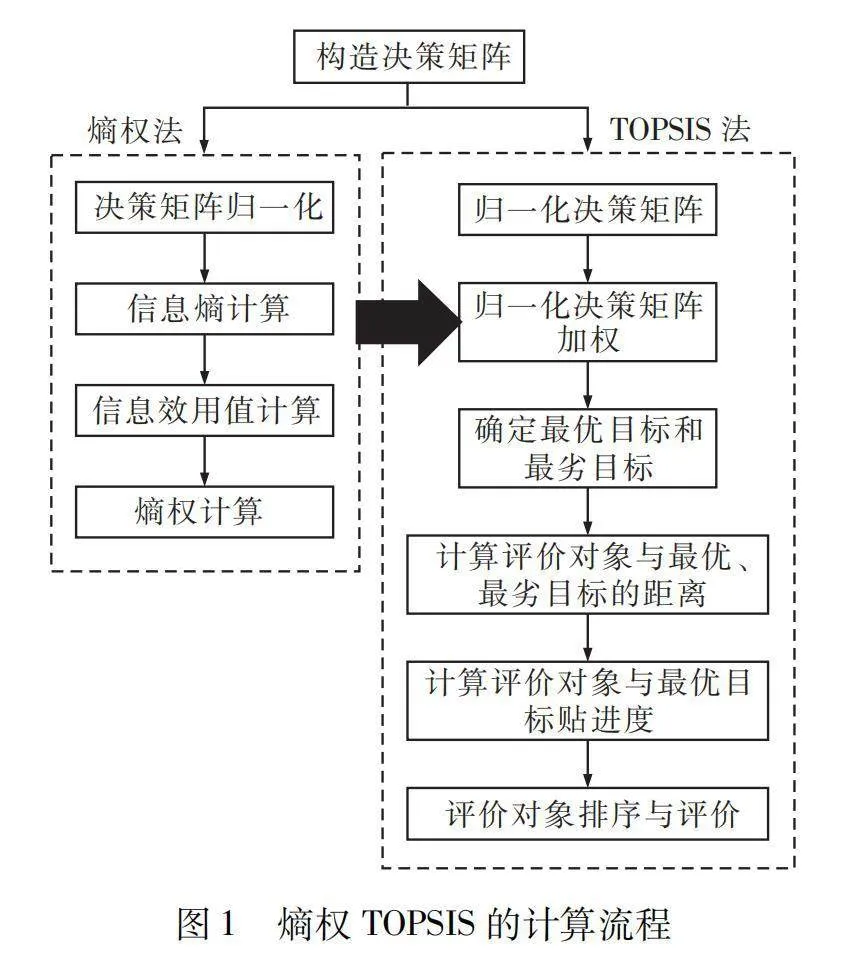
将式（12）计算获得的权重带入式（8）中，即可获得经熵权法修正的TOPSIS排序结果。熵权TOPSIS的计算流程如图1所示。

1.3 熵权TOPSIS模型多准则决策验证

在对教师进行多准则绩效考核时，更侧重于对在不同指标项取得突出成果的老师进行平衡，以发挥教师的专长和特点。为了验证熵权TOPSIS模型对教师多准则考核的可行性，构造式（13）所示由五位教师在5项指标中的得分构成的决策矩阵，其中每位教师的五项指标得分从1～5，而5项指标中教师的得分同样分布于1～5。该矩阵表示每位教师在不同的指标中都有自己的优势，而同样在其他指标中具有劣势。

采用式（9）～（12）的熵权法确定计算可以得到五项指标的权重均为0.2，该结果符合预期，即每项指标中的待评价值均从1～5，其具有相同的变异程度。采用该权重及式（1）～（8）的TOPSIS方法，计算得到的被评价对象与最优目标值的贴近度C^*均为0.2，即各位教师的表现相同。该结果表明，虽然五位教师在不同指标中的得分不同，但分别在自身具有优势的指标项取得较好成绩，因而能够获得相同的评价。该理想状态下的计算结果表明采用熵权TOPSIS模型可以对教师进行多准则绩效考核，发挥教师的特长。

2 教师多准则绩效评价应用与分析

2.1 教师多准则绩效评价体系与样本数据

教师绩效评价体系中的评价指标具有指挥棒的作用，因此学院和学校根据自身实际情况选取，以使教师的工作与学院和学校的发展目标和日常工作相契合。西安科技大学××学院以人才培养、科学研究和社会服务作为一级指标，并在该指标下设置二级指标及其观测点构建教师综合绩效评价指标体系如图2所示，各二级指标涵盖的主要观测点及量化标准见表1～表3，通过评价指标对应观测点的量化积分对教师进行绩效考核。选取该学院10名教师某一年度的量化积分值作为样本数据，采用图2中C～C共6项指标对教师进行评价，样本数据和评价指标见表4。

2.2 评价指标熵权计算

采用式（1）和式（9）对表4中的数据进行标准化处理，再根据式（10）～（12）计算得到的多元绩效评价指标的信息熵和熵权见表5。

计算得到的权重中，教师指导学生科技活动C具有最大的权重和最小的信息熵，表明教师在该项考核指标中的差异性较大，在考核中权重将占到53.43%。论文与著作指标C的权重排序为2，其权重为18.36%。评教的信息熵为1，表明待评价对象在该项的差异性较小，其对综合评价的权重最小为0.01%。

表5 绩效评价指标信息熵与熵权教学C评教C科技活动C科研C论著C服务C信息熵0.943 91.000 00.626 40.877 70.871 60.981 2熵权0.080 20.000 10.534 30.174 90.183 60.026 9熵权排序461325

2.3 评价对象排序与分析

表4中的数据按照式（2）归一化，并采用式（3）进行加权处理后得到的加权决策矩阵为

采用式（5）计算得到的最优目标和最劣目标分别为：

A⁺=［0.056 5，0.000 0，0.500 2，0.126 3，0.108 3，0.011 5］

A^－=［0.010 7，0.000 0，0.000 0，0.015 3，0.000 0，0.004 0］

采用式（6）和式（7）计算得到的样本数据绩效评价等级见表6，熵权TOPSIS排名与原积分排名有较大差异。教师A的科研指标C积分最高，社会服务指标C也较高，因此在积分排名体系中该教师位列第一。但由于教师在科研C及社会服务C两项指标的积分差异性不太大，造成这两项评价指标在熵权TOPSIS评价体系中的权重较小，合计仅占21.18%。而教师A在指导学生科技活动C与论著C两项合计权重占71.79%的指标中积分仅为0.5分，造成其排名下滑至第三。教师A由于在权重最高的指导学生科技活动C指标项积分远超其他教师，且在其他评价指标的积分较为均衡，其排名由第五跃升至第一。原积分排名第二的教师A由于在指导学生科技活动指标C中的积分较低，且在教学C与论著C两项指标的积分没有达到中位数的水平，其排名下滑至第五。而原排名第十位的教师A则由于在指导学生科技活动C与教学C两项指标中具有较高的积分，排名跃升至第二。

表6中熵权TOPSIS绩效排名计算结果表明，权重对排名有重要影响，根据熵权法计算得到的权重，依赖于各评价指标的差异性。如果评价对象在某一观测指标中的差异不大，则其在整个评价中的权重会很小，例如表4中评教指标。而那些差异性大的评价指标，则会占据高权重比，在评价中发挥重要的作用，例如表4中的指导学生科技活动指标。在熵权TOPSIS绩效排名中，通过欧式距离判断评价指标与最优解和最劣解之间的距离判断指标的优劣，因此评价对象在同一评价指标内即使排名第二，但是如果与最优解之间有较大的差值，根据式（10）和（11），其对目标的贴近度也会减小。

此外，熵权TOPSIS绩效评价也倾向于向参与度低或者某项成果特别突出的评价者倾斜。但由于在TOPSIS中存在通过计算与最劣解之间距离对待评价对象的排序进行惩罚的机制，待评价对象如果存在某项指标的缺失，将会对评价结果产生影响。

3 熵权TOPSIS评价影响因素分析

3.1 熵权对TOPSIS评价结果影响

在式（4）中引入了熵权对TOPSIS的归一化决策矩阵进行修正，为了衡量熵权引入对原始TOPSIS排名的影响，采用欧式距离表征其影响程度，

式中，u为待评价对象排名变化后与原始排名之间的欧式距离；k⁰和k分别为待评价教师A原始排名与变化后的Y0h52B06aYvpVFejrDtNMiO85nE0TjTyMXOAg9VmUKQ=排名。

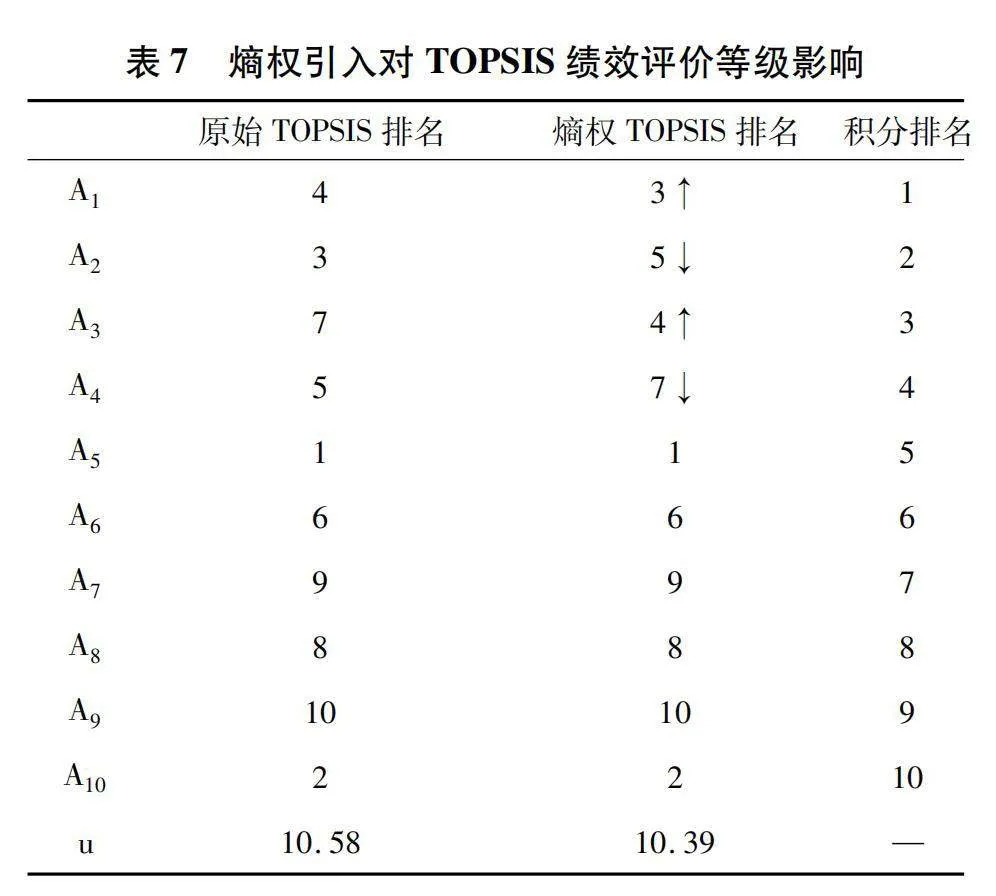
表7对比了熵权引入造成的原始TOPSIS模型排序结果变化，多名教师的排名受到了影响。采用式（14）计算得到原始TOPSIS排名及熵权TOPSIS排名与积分排名之间的距离分别为10.58和10.39，熵权TOPSIS排名与原始TOPSIS排名之间的距离为4.24，熵权引入对排名产生了较大影响。从单一个体分析，教师A受引入权重影响最大，由于教师A在教学C、科研C中的表现均不好，即使论著C与服务C两项指标中具有较高的积分，在TOPSIS模型中该教师排名仅为第七。但是引入熵权对权重进行调整后，A教师不占优势的教学C及科研C指标权重下降最多，而该教师表现较好的论著C指标权重下降，因此其排名由第七上升至第四。教师A和A则由于在论著C项的表现不佳，熵权引入使论著C项的权重增大，其劣势被放大，其占优势的科研C项权重减小，其优势被所需，造成他们的排名均下降两位至第五和第七。该结果表明熵权引入TOPSIS模型后，其权重向内部差异大的指标倾斜，在内部差异大的指标中表现优秀的待评价对象更容易取得好的排名。

3.2 评价指标量化标准对评价结果影响

依据表1每10个教学工作量计1分的业绩量化标准，考虑到TOPSIS方法在进行多准则决策时不需要指标具有相同的量纲，因此直接采用工作量值作为C的量化指标计算权重见表8，可以看出，给予C指标相同的乘数后，原指标体系的权重不发生变化，不对排名结果产生影响。这是由于依据式（15）定义的指标离散系数v不发生变化。

式中，s和x^-分别为评价指标j内待评价教师量化积分的标准差和均值。

无论是按照表4中C指标量化数据，还是按照C指标量化数据乘以10得到的原始工作量，采用式（15）计算得到的数据离散系数均为0.594 6，表明给予指标项数据一个乘数后，数据内部的离异程度不发生变化，因而不会对权重和排名产生影响。

采用表4数据计算时，教师的评教数据C区间为[84，88]，为此考虑将评教数据同时减80，将数据平移至[4，8]的区间内，计算得到的指标熵权见表8。数据区间平移后，评价指标的权重发生了变化，评教指标C的权重上升至1.13%。这是由于指标数据的平移使指标内数据的差异性变大。根据式（15）计算得到平移前后C指标的离散系数分别为0.014 6和0.197 6，数据平移后的离散程度增大，因而其对评价权重产生了影响。但由于其离散程度与其他数据相比仍然较小，因而没有改变排名。

由此可见，给予评价指标量化数据乘数不会对评价结果产生影响，但数据偏移会对权重产生影响，并会对评价结果产生影响。

3.3 评价指标变化对评价结果影响

表9给出了评价指标变化后各剩余指标间熵权的变化。首先评价指标权重排序不受评价指标减少的影响，依次删除C～C中的某一项评价指标后，剩余评价指标的权重次序不会发生变化。由于在熵权TOPSIS模型中，指标间的权重分配由各指标待评价对象的差异程度决定，因而在评价对象数据保持不变的情况下，评价指标减少不影响剩余评价指标的权重排序。其次，剩余评价指标将获得被删除指标的权重，表10给出的剩余指标权重变化增量变化表明，剩余指标获得权重的大小排序与原权重指标排序相同，即指标原有的权重越大，在评价指标减少后新增的权重越多。在评价指标减少后，权重更趋于向待评价对象差异化程度高的指标集中，使在该指标占优势的待评价对象获得好的排序。

以上权重变化考虑的是减少某项评价指标对评价结果的影响。据此可以推出，在指标体系中增加新的评价指标，首先，原指标的权重排序不受影响，新增指标将按照待评价对象的差异程度插入原指标权重排序中。其次，新增指标将从原指标中获得权重，原来指标的权重越大，其损失的权重也越大，即新评价指标的加入会缩小原高权重指标的优势。

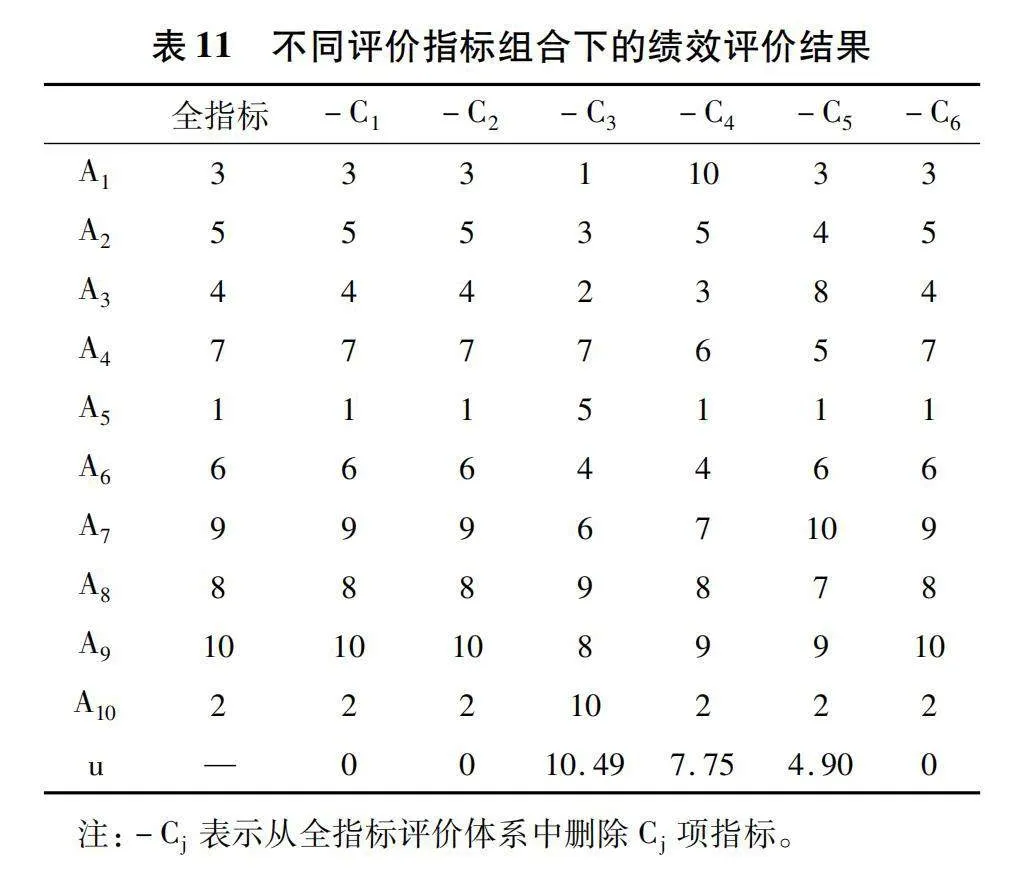
评价指标减少造成的权重变化，使评价结果的次序发生了表11所示的变化。可以看出评价指标C，C及C的变化对评价结果没有产生影响，这是由于这些指标在全指标体系的权重都很低，三者中最高权重教学指标C仅占8.02%，它们的增减对指标体系影响不大。分别剔除指标指导学生科技活动C、科研C及论著C后，教师排序的变化量分布为10.49、7.75与4.9，指导学生科技活动指标C引起的排序变化最大。这是由于指导学生科技活动指标C在原全指标时的权重超过53%，该指标变化对排名的影响最大。教师A和A从全指标前二分别下滑至第五和第十，这与他们在被删除的指导学生科技活动C指标中得分最高相关。教师A则由于在科研C与服务C两项指标中较高的分值，从第十跃居第二。A教师则由于在各指标中的表现均处于中上水平，其排名从第四跃居第二。当分别剔除论著C与服务C两项指标时，同样会对在该指标具有优势的待评价对象产生不利影响，使其排名下降。

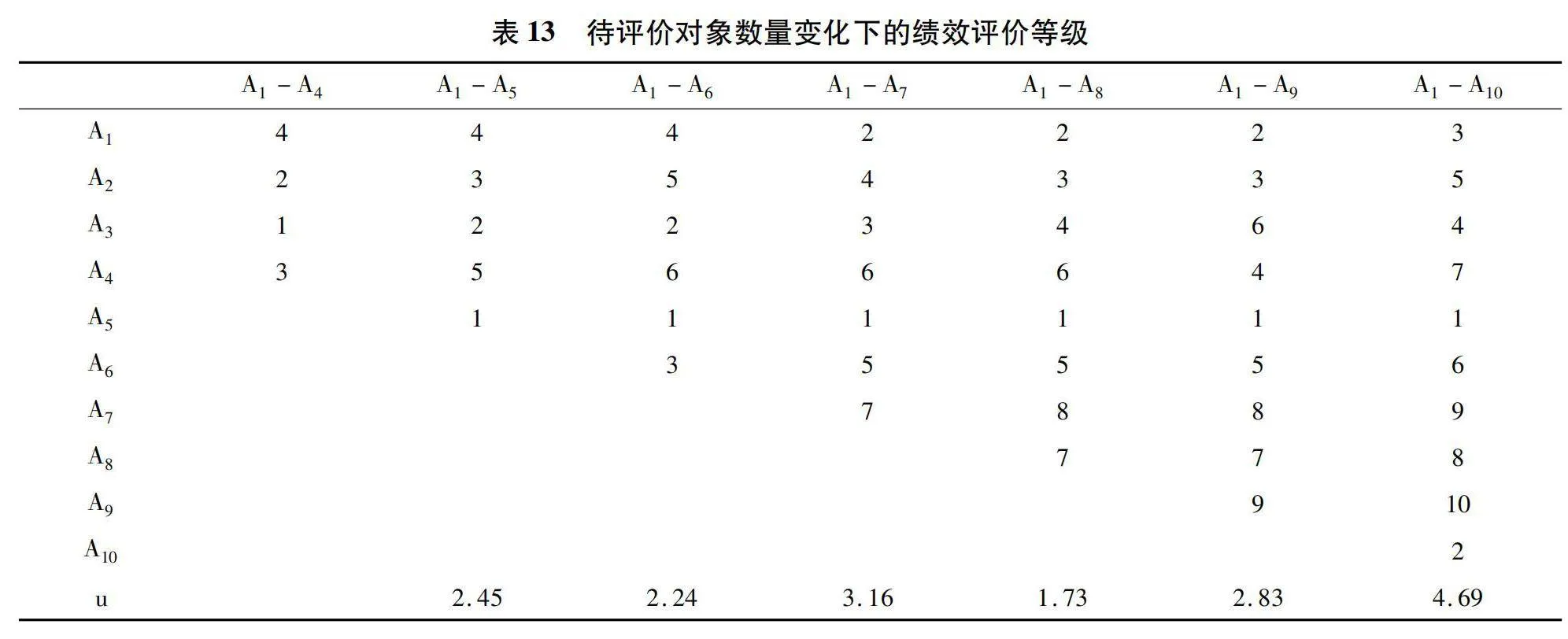
3.4 待评价对象数量

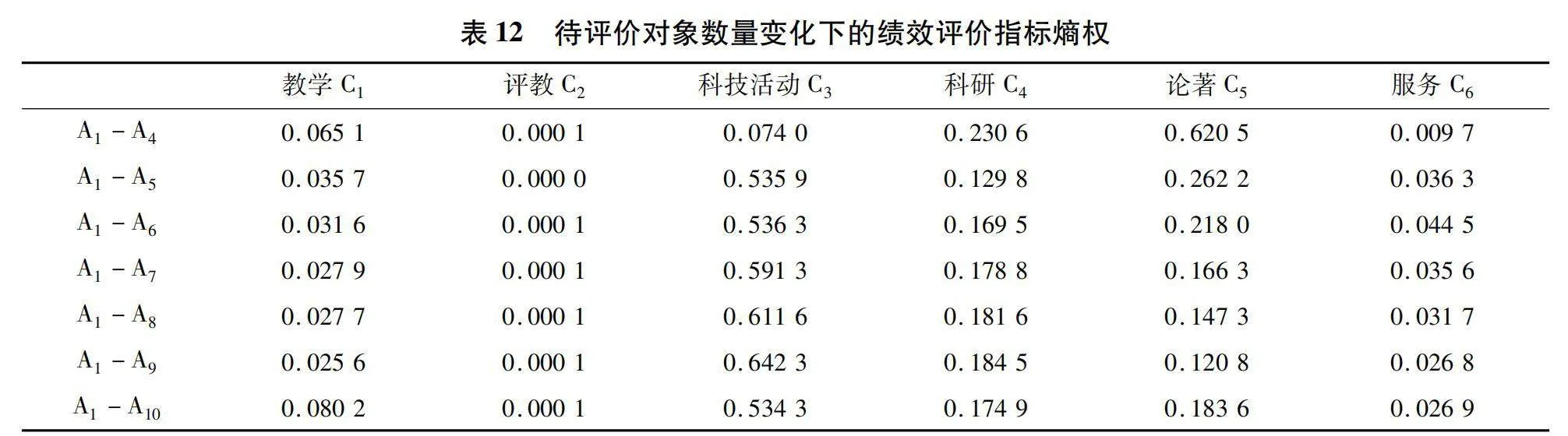
表12和表13分别列出了待评价对象数量从4名逐个增加到10名后，各指标熵权及待评价对象排序的变化。待评价对象只有A-A这4名教师时，指标项论著C权重达到了62.05%，因而在指标中占据优势的A教师位列第一。教师A虽然凭借最高的科研积分在总积分排名中位于第一，且该项指标权重达到了23.06%，但由于其在论著C指标项积分为0，在熵权TOPSIS中的排序将为第四。增加教师A后，权重最高的指标变为指导学生科技活动C，权重达到53.59%；原来权重最高的C项降低至26.22%，科研C指标的权重降至12.98%，这使得在指导学生科技活动中占据优势的A教师跃居第一；A教师由于论著C指标权重的降低，排名由第一变为第二；A教师则由于在合计权重占79.81%的指导学生科技活动及论著两项指标中表现较差，排名位于第四位。

待评价对象数量变化造成的排名顺序的变化，源于绩效评价指标熵权的调整。而熵权的变化取决于各评价指标内数据的差异性。如果新增待评价对象后，会造成某项评价指标差异性的显著变化，则该评价对象的引入会对评价指标的权重和评价结果产生显著影响。表12中距离u的计算结果表明，教师A的引入对排序变化的影响最大，这是由于教师A在指标教学C中具有最高的积分，该教师加入排序后，使教师在指标教学C中的积分差异性增大，该指标权重增大。教师A的引入导致的排序变化程度居第二位，这是由于该教师在指标指导学生科技活动C项积分为0，使C项内部数据差异性增大，而权重最大的该项进一步增大。教师A在指导学生科技活动C项的成果显著高于原有A-A教师，使该项指标间的差异性变得最大而获得最大权重，进而影响评价结果。教师A的引入由于没有对原评价指标的差异性产生显著影响，因而他的加入对于各指标的权重分布及教师的排序影响不大。

表12和表13分析待评价教师从4名增加到10名时熵权和排名的变化，该数据的样本量仍然较小，在实际应用时待评价教师数量会更大，指标数据的变化范围和离异程度变化也会更大。将教师的样本数量增大到100名后各指标的信息熵、熵权的变化见表14，选取的10名教师的排序见表15。采用式（14）计算得到小样本和大样本熵权离散系数分别为0.997 0和0.809 9，表明大样本条件下，各指标的权重分布更为均衡。指标项教学C与指导学生科技活动C的信息熵增大，表示这两项指标内部数据的差异性减小，造成其权重的降低；指标科研C、论著C及服务C的信息熵减小，这些指标内部数据的差异性增大，引起它们权重的增大。最终使论著C与科研C两项成为权重最大的指标，权重分别为38.24%和25.25%；小样本条件下权重最高的指导学生科技活动C指标，权重从53.44%降低至30.52%。由此可知，样本数量的大幅增加，会使评价结果更为合理，但无论在何种条件下教学C及服务C项指标的权重均较小，表明这两项指标在教师业绩评价中发挥的作用有限。

4 结语

1）熵权TOPSIS模型中内部差异化大的指标具有高权重，并使在这些指标中表现突出的教师排升，使评价结果明显区别于积分排序。评价指标的增减不影响原评价指标权重排序，且原评价指标权重减少或者增加的量与原指标权重排序成正比。给予评价指标量化数据乘数不会对评价结果产生影响，但数据偏移会对权重产生影响，并会对评价结果产生影响。待评价对象数量变化对评价指标权重和评价结果的影响取决于新增或者减少评价对象对评价指标内部数据差异性的大小，该差异性越大，评价指标权重和评价结果受影响越大。大样本条件下评价指标的权重分布更为均衡。

2）应依据学科与专业特色，分类考核与评价。本例中指导学生竞赛指标权重很高，其原因为教师在该项指标的积分差异性所致，而该差异性是由于学科间的差异造成的，有些教师隶属于公共基础课教师，没有专业学生或者缺乏相关的竞赛，造成该指标的缺失。这会造成同时使该指标的权重增大，违背评价体系最初的设计目标并造成评价不公。由于每个学科领域的历史文化及学科特点不同，其用来与学术社群沟通的形式和取得的业绩形式不同，如果采用统一的标准与指标，会抑制学科发展的活力并加剧不同学科间的不当竞争，使学科彼此间的沟通产生紧张关系，影响学院的整体发展。因此建议对学科分类建立考核体系，选择适合各学科自身特点的指标和观测点。

3）建议结合学院特点和发展，平衡导向性和多元性。业绩评价具有指挥棒的作用，学院在选取评价指标和观测点时通常着重考量其发展目标的达成，将学校对学院的考核目标与任务导向具体为教师的业绩指标。但这样会导致教师按照评价标准及其指标来框定个人的工作内容，忽视那些无直接相关的社会性、情感性与道德性的发展活动。因此应考虑评价功能取向多重性的特点，选取指标时既体现学院的发展目标，又整合教师职业道路灵活性和个体差异，满足教师的专业成就与职业发展诉求，形成多层次、多方位、多角度的评价，实现评价效率与评价目标的统一。

4）应依据评价目标与原则，合理构建业绩量化标准。在采用业绩量化对教师进行评价时，通常将教师的教学、研究与社会服务等业绩表现量化赋分，以衡量教师学术产出价值和社会效用。但不合理的量化标准会造成评价指标失效，引起评价结果偏离评级体系的初衷。如本例学评教和教学工作量指标，由于其内部数据差异性小，造成其指标权重的降低，使其对最终评价结果的影响降低。因此在制定业绩量化标准时，不仅要合理设计业绩量化标准，拉开同一指标间教师业绩的差距，同时还要均衡各指标数据差异性的大小，避免造成指标权重过小而失效，进而达到评价的导向性和多元性的目标

5）建立的高校教师多准则定量评价体系主要采用熵权TOPSIS方法进行评价分析，但由于该方法使用欧氏距离进行判断，而不考虑指标间的相关性，指标间的相关性会对评价结果产生影响。文中以现有指标体系为基础讨论了评价指标量化标准、评价指标数量、评价对象数量变化对评价结果的影响，从结果中可以看出教学与评教等指标的权重过小，说明当前的评价指标体系仍不完备，仍需针对评价对象分类、评价指标与观测点的合理设置、评价指标量化标准与差异化控制等方面进一步研究，以使建立的教师绩效定量评价机制真正实现多准则评价的目的，避免“唯科研、唯论文”等考核指标的片面化，使不同特长的老师均能在考核中获得自我成就感及工作满意度，激发其最大潜能，促进相关专业和学科的高质量发展，提高院校的核心竞争力。

参考文献：

[1] 周玲，王欣怡，张慧婷.高校发展性教师评价的逻辑困境与价值回归[J].中国人民大学教育学刊，2024（02）：33-53+4.

[2]王丹慧.地方中小型高校教师绩效评价现状及对策探讨[J].南华大学学报（社会科学版），2011，12（05）：75-77.

[3]郭涛.高校教师敬业度影响因素及其与工作绩效的关系研究[D].天津：天津大学，2013.

[4]鞠晓红，牛熠.基于OKR的高校教师绩效管理模型及实施路径研究[J].黑龙江高教研究，2020，38（02）：82-87.

[5]高金勇.高校教师评价中的量化维度及其纠偏[J].江苏高教，2024（03）：44-52.

[6]周双喜，谢延浩.均衡思维下高校教师绩效评价的原则与方法[J].黑龙江高教研究，2018，36（10）：108-113.

[7]郑丹.善治理论视阈下高校教师绩效评价的问题与优化策略[J].高教论坛，2022（10）：13-16.

[8]苏强，蔡晓卫.效率还是价值——高校教师评价制度的逻辑困境及其张力调适[J].华东师范大学学报（教育科学版），2023，41（06）：133-141.

[9]杨帆.区域特色研究型高校教学科研岗教师“四维一体”绩效评价模式研究[D].上海：上海师范大学，2020.

[10]张宁.高校教师绩效评价的定性分析及数学模型[J].江苏社会科学，2012（S1）：81-84.

[11]袁耀东，许红艳，何贝贝.回归教育本质——高校教师绩效评价的多维度改革路径探析[J].公关世界，2024（10）：116-118.

[12]刘亚兰.高校教师绩效评价指标体系的完善与优化[J].北京财贸职业学院学报，2021，37（02）：50-54.

[13]黄英婉，王敬涛.高校教师绩效考核指标评价体系的构建[J].沈阳大学学报（社会科学版），2016，18（03）：282-285.

[14]周双喜，谢延浩.多元主体视角的教师绩效评价系统模型[J].黑龙江高教研究，2015（04）：23-25.

[15]TAHERDOOST H，MADANCHIAN M.Multi-criteria decision making（MCDM）methods and concepts[J].Encyclopedia，2023（03）：77-87.

[16]SHAHSAVARANI A M，ABADI A M E.The bases，principles，and methods of decision-making：A review of literature[J].International Journal of Medical Reviews，2015（02）：214-225.

[17]陈秋涵.基于AHP的高校“三全育人”绩效评价体系的研究[J].贵州师范学院学报，2022，38（09）：20-24.

[18]傅艳梅.应用型本科院校专职教师绩效考核评价体系构建及应用[J].豫章师范学院学报，2024，39（01）：63-66.

[19]杨妍，张忻.基于AHP-CRITIC法与系统动力学理论的高校教师绩效评价系统模型实证研究 [J].西部素质教育，2024，10（02）：13-17.

[20]鲁明浩.基于模糊综合评价模型的教师绩效考核研究[J].黑龙江科学，2024，15（01）：59-61.

[21]郭涛，林盛，刘金培.高校教师科研绩效评价——一种多准则决策分析模型[J].统计与决策，2012（09）：66-69.

[22]付沙，孙光，周航军，等.基于粗糙集和条件信息熵的高校教师绩效评价研究[J].齐齐哈尔大学学报（自然科学版），2016，32（03）：29-35.

[23]刘叶，王帅，周庆忠.基于RS与SVM的高校教师绩效评估模型的构建与仿真[J].物流技术，2018，37（07）：152-156.

[24]MADANCHIAN M，TAHERDOOST H.A comprehensive guide to the TOPSIS method for multi-criteria decision making[J].Sustainable Social Development，2023，1（01）：2220.

[25]ĢELIKBILEK Y，TÜYSÜZ F.An in-depth review of theory of the TOPSIS method：An experimental analysis[J].Journal of Management Analytics，2020，7（02）：281-300.

[26]HWANG C L，KWANGSUN Y.Multiple attribute decision making：Methods and applications a state of the art survey[M].Berlin：Springer-Verlag，1981.

[27]CHENG S，CHRISTINE W C，GUO H H.Using multiple criteria decision analysis for supporting decision of solid waste management[J].Journal of Environmental Science and Health，Part A，2002，37（06）：975-990.

[28]ZANAKIS S H，SOLOMON A，WISHART N，et al.Multi-attribute decision making：A simulation comparison of selection methods[J].European Journal of Operational Research，1998，107（03）：507-529.

[29]SELAHATTIN K，ALTUNTAS S，DERELI T.Comparing the innovation performance of EU candidate countries：An entropy-based TOPSIS approach[J].Economic Research-Ekonomska Istraživanja，2017，30（01）：31-54.

[30]CHEN P Y.Effects of the entropy weight on TOPSIS[J].Expert Systems with Applications，2021（168）：114186.

（责任编辑：王强）