浅析泰勒公式在高中数学的应用

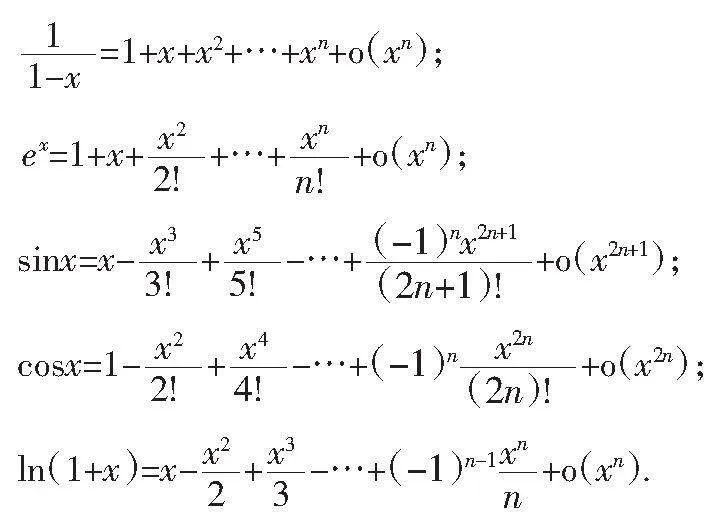
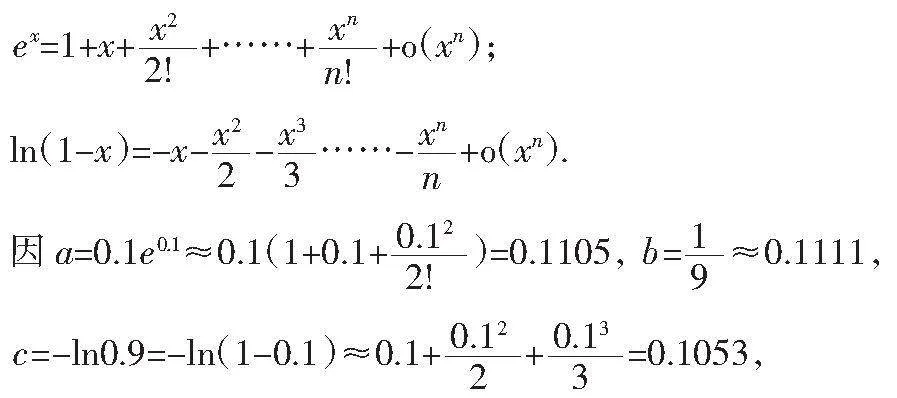
摘 要：泰勒公式是现代数学分析的重要内容，在研究和分析各种数学问题中有着重要的作用，其理论是研究函数极限和估计误差等方面的重要工具.近几年来高考的热门题型比较大小，一般是先构造模型，然后代入数值运算及比较.学生往往在选择函数模型方面有一定的难度.灵活正确地使用泰勒公式，可以使得解题更加方便，达到事半功倍的效果.探讨泰勒公式在高考试题等知识领域的应用有助于学生拓展思维、锻炼能力.

关键词：泰勒公式;比较大小;高中数学

泰勒公式是数学分析中一个非常重要的内容，其基本思想是用多项式逼近已知的函数，而这个多项式的系数一般由给定函数的各阶函数导数确定.它是研究函数极限与估计误差等方面的重要工具[ 1 ]，正确利用泰勒公式来解决相关问题，可以达到事半功倍的效果.近几年高中数学函数问题解决过程中应用泰勒展开式案例颇多.学习泰勒公式，并能学以致用可以更便捷解决函数类相关问题[ 1 ].

1 常用函数的泰勒展开式

首先，了解泰勒展开式是将一个在x=x0处具有n阶导数的函数f（x）利用关于（x-x0）的n次多项式来逼近函数的方法[ 2 ].

1.1高中数学学习中，面对复杂的函数问题时，常用函数泰勒展开式有以下几个：

2 泰勒公式在近年高考试题中的应用

2.1 教材中的应用

在人教版《普通高中教科书·数学》必修第一册A版（2019年版本）中第五章《三角函数》复习参考题5第26题，英国著名的数学家泰勒发现了三角函数拓展公式：

运用泰勒公式在一些求具体函数实际数值时（尤其是当项数比较少时函数取值）计算很方便.

2.2 高考中的常用泰勒展开式及其应用

泰勒公式是高等数学的知识，在高中数学学习中适时拓展应用，可以起到事半功倍的效果.在高中数学命题中的常用模式：（1）从泰勒公式的本身内涵及其一般常用结论来设计题目.对于这类题目的命制，要求命题人在命题时必须对泰勒公式的内涵全面深入了解，然后提炼出与中学数学相挂钩的常用函数.从泰勒公式一般结论出发，常考虑近似取值前几项，通过逆推和具体化来命题，将泰勒公式进行简化和近似取值，并进行四则运算.（2）直接套用泰勒公式展开式进行题目命题.这类题目可以直接用泰勒公式近似取值，检验结果是否正确[ 2 ].

高考中的常用泰勒展开式有：

从以上案例归纳出，对任意函数进行泰勒展开，并不一定用到f（x）的具体表达式，而结论往往是一般性的，试题的命制者出发点和思考点是奠定在综合思维基础上，将平时常用一般性的结论引进到某些特定函数之中，然后构造得到一些结构整齐匀称的式子.这类题目是多重思维的叠加，综合考察学生的创新思维能力，通常起到高考选择题、填空题的压轴作用[ 3 ].对大部分学生来说此类试题是陌生的，与他们平时训练的题目有所不同，非常规思路.这会使大部分学生感到困难，无从下手，束手无策，尤其在考试中有一定的压力.而解决这类问题只要学生平时多了解一些泰勒公式的应用，通过放缩等方法，比较两个式子的大小，也就迎刃而解.

2.3 高考真题案例分析

A、a<b<c B、c<b<a C、c<a<b D、a<c<b

分析：从已知条件的中，选择常用函数泰勒展开式得知

从以上分析中得c<a<b. 故选：C.

A、a<b<c B、b<c<a C、b<a<c D、c<a<b

分析：从已知条件的中，选择常用函数泰勒展开式得知

从以上分析中得： a<b<c. 选A.

A、a<b<c B、b<c<a C、b<a<c D、c<a<b

将x=0.01，x=0.02，x=0.04代入以上泰勒公式即可得a，b，c值，

易得b<c<a. 故选：B.

由以上三个例子分析可知，泰勒公式在估值方面（尤其项数取值比较少时）一般非常准确，所以，在碰到几个超越函数比较相近又一时无从下手时往往可以考虑运用泰勒公式.不难看出，泰勒公式在比较大小这类问题时，起着非常重要的作用，教师在高中实际教学中可以借助课后习题或平时拓展知识引入一些泰勒公式的知识，拓展学生思维，提升学生思维能力，引发学生学习兴趣.

总之，利用泰勒公式对求解一些难度比较大的试题可以起到事半功倍的效果.利用泰勒公式前提是抓住函数的基本特征，灵活合理构造函数.在构造函数时，尽量不用除式，多用乘积表达逐步引入泰勒公式进行估计，在让学生了解估计与计算这类近似问题时会很方便，而且对于我们研究某些具体函数会起到一定的指导作用.近年高考中，比较喜欢考查的是比较实数大小，此时考虑运用泰勒公式可以很快解决问题.这类问题一般出现在选择题或填空题，常见的泰勒展开式也可以运用于解决证明题或者是导数大题[ 3 ].

3 价值取向

近年来，在各级各类考试和高考命题中，命题者都很喜欢不等式ex≥x+1，lnx≤x-1的应用，上面的不等式可以利用图像说明结论.追其根本，这两个不等式在某种程度上都来源于高等数学中的泰勒展开式，在高等数学中，泰勒公式利用函数在某点的信息，描述其附近取值的公式.如果函数连续且平滑，那么泰勒公式可用这些导数值作为系数构建一个多项式.

向量、导数、概率统计等等以前在大学才能接触到的知识点，已经以探索、拓展、提升等形式渗透进新教材、新高考.高考这一极其重要的选拔人才的考试中，高等数学常常作为高考命题出发点，考查学生的知识迁移能力，综合分析问题能力以及应用能力.培养并提高学生的创新思维，不仅要让学生对各种常规题型、基础题型等加以训练，还要培养学生换位思考问题的能力，努力站在命题者的角度去考虑问题[ 4 ].高中教师要用新课程标准审视常规教学，不断地提高教研能力.

参考文献：

[1] 孔珊珊. 泰勒公式在数值计算中的应用[J].济宁学院学报，2011，32（3）：70-72.

[2] 潘劲松. 泰勒公式的证明及应用[J].廊坊师范学院学报，2010，10（2） ：16-21.

[3] 陈炳泉. 一道高考导数题的思考与探索[J].数学通报，2021，60（3）：59-62，66.

[4] 陈炳泉. 基于数学核心素养的高考一类常见导数题思考与探索[J].福建中学数学，2023（4）：45-48.