基于改进特征模态分解和谱峭度的滚动轴承故障诊断

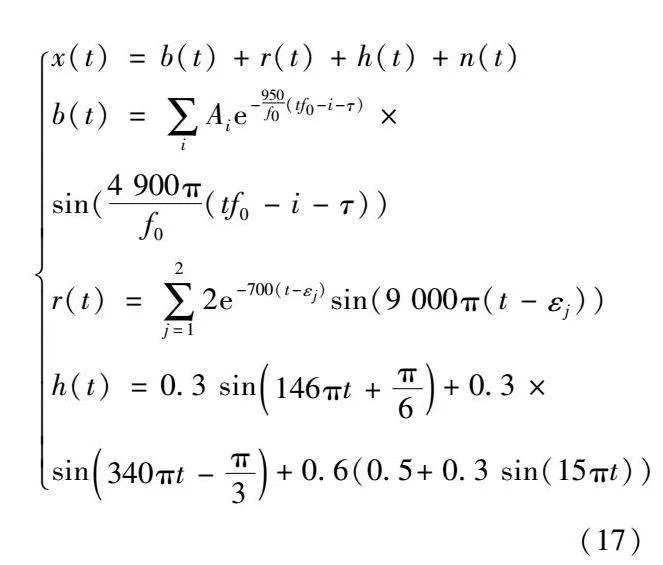
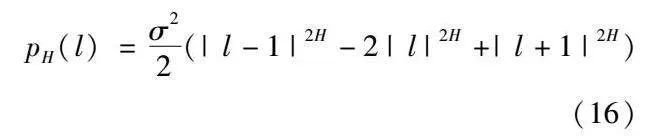
文章编号1000-5269（2024）05-0032-09 DOI：10.15958/j.cnki.gdxbzrb.2024.05.05

摘要：考虑到滚动轴承的故障信号通常表现出非平稳、容易受到干扰而无法被有效诊断的特点，提出一种改进特征模态分解（featuremodedecomposition，FMD）和谱峭度（spectralkurtosis，SK）的滚动轴承故障特征提取方法。首先，对FMD的滤波特性进行研究，合理选择其两个重要输入参数；其次，采用FMD对滚动轴承故障信号进行处理，得到多个模态分量的分解结果，并通过计算各模态分量与原始信号的灰色关联度及互信息来选择最佳模态分量；最后，通过谱峭度对最佳模态分量进行带通滤波来凸显信号中的周期性冲击成分，从而有效实现故障特征频率的提取。通过分析仿真信号和实验数据的结果，发现提出方法可以有效提取故障信号特征频率的包络谱峰值和倍频谐波部分，且相比于其他方法，谱线特征更加明显，说明使用该方法对滚动轴承出现的故障进行诊断是可行的。

关键词：特征模态分解；谱峭度；灰色关联分析；滚动轴承；故障诊断 中图分类号：TH133.33 文献标志码：A

滚动轴承是一些现代机械设备（风力发电机、高铁列车）的核心零部件。通常情况下这些机械设备的工作条件恶劣、工况复杂，这使得滚动轴承容易出现各种故障，从而影响到机械设备的正常工作，因此有必要对滚动轴承故障进行监测和诊断［1］。其中，滚动轴承故障的信号是包含冲击和噪声干扰的非平稳复杂信号，故障特征提取是故障诊断至关重要的一v9DrOt1v8tknVACffEIanHgsQhSpN3/nJj3CvTlXj+E=部分。

许多学者在信号处理和故障诊断领域进行了广泛研究，也取得了颇多成果。如稀疏表示［2］、谱峭度（spectralkurtosis，SK）［3］、最小熵解卷积（minimumentropydeconvolution，MED）［4］、最大相关峭度解卷积（maximumcorrelatedkurtosisdeconvolution，MCKD）［5］、一些传统时频分析方法和自适应分解方法。一些常见的自适应分解方法有经验模态分解（empiricalmodedecomposition，EMD）［6］、变分模态分解（variationalmodedecomposition，VMD）［7］等。与其他方法相比，自适应分解方法凭借其在不需要先验知识的情况下能将多分量信号分解为多个单分量信号的优势而得以广泛运用。

其中，EMD用于处理非平稳信号，并在故障诊断、医学数据处理和图像信号处理等领域得到广泛应用。虽然这种方法十分有效，但是它也存在着一些缺点，比如端点效应和模态混淆。为此，相关学者进行研究并提出了一些改进EMD方法，主要通过在分解过程中加入辅助噪声并通过多次叠加来减少信号本身噪声的干扰，一定程度上解决了模态混淆现象并改善分解性能。为了有效地克服EMD端点效应和模态混淆等缺点，DRAGOMIRETSKIY等［8］提出了VMD，该方法以维纳滤波、希尔伯特变换等数学理论为基础，通过非递归筛选将原信号进行分解，但是VMD的分解性能在很大程度上受到模型参数选择的限制。

在此背景下，受自适应分解方法局限性和解卷积原理的启发，MIAO等［9］近年来提出了一种新的信号分解理论——特征模态分解（featuremodedecomposition，FMD）。该方法本质上是设计一系列自适应有限脉冲响应（finiteimpulseresponse，FIR）滤波器组，迭代更新滤波器系数，使滤波信号无限接近解卷积相关峭度的目标函数，并采用自相关函数估计信号的故障周期，分解故障信号为若干个模态分量。该方法不仅同时考虑信号的脉冲性和周期性，而且对干扰信号具有一定的鲁棒性。

但是FMD分解性能受到两个重要输入参数（模态个数n和滤波器长度L）的影响，同时其分解后的结果容易受到虚假分量的干扰。因此，本文提出了一种改进FMD和谱峭度的故障特征提取方法。首先，研究FMD的输入参数对其分解性能的影响，合理选择参数，采用FMD对故障信号进行分解；其次，通过灰色关联分析和互信息（mutualinformation，MI）结合来筛选出分解后的最佳模态分量；最后，利用谱峭度分析并进行带通滤波来凸显故障冲击成分。仿真信号和轴承故障数据实验结果表明，所提方法能在轴承故障信号中有效地提取到故障特征，能够实现对滚动轴承故障的诊断。

1基本原理介绍

1.1特征模态分解

FMD包括FIR滤波器组设计、滤波器更新、故障周期估计和模态选择等过程。FMD流程如图1所示。其具体实现过程如下：

1）加载原始信号x，设置FMD的分解模态个数n、滤波器长度L等参数。

2）通过K个汉宁窗初始化FIR滤波器组，初始化迭代i=1，建议K∈［5，10］。

3）根据uik=xfik来得到滤波信号。其中：k=1，2，…，K；*表示卷积运算；fk表示第k个FIR滤波器。

4）使用原始信号x、分解模态信号uik和估计周期Tik来更新滤波器系数。其中：估计周期Tik是由uik的自相关谱在过零点后达到局部最大值Rik的点来更新滤波器系数，完成一次迭代并设置i=i+1。

5）判断当前迭代次数是否达到预期迭代次数。如果达到则进入步骤6），否则返回步骤3）。

6）计算每两个模态分量之间的相关系数CC（correlationcoefficient，CC），构造一个K×K矩阵CC（K×K）。选择具有最大相关系数的两个相邻模态分量，并通过估计周期Tik来计算它们的相关峭度CK（correlatedkurtosis，CK），在两个模态分量中选择具有较大CK的模态，设置K=K－1。

7）判断当前模态个数K是否达到预设模态个数n。达到则进入步骤8），否则返回步骤3）。

8）获得n个模态分量作为最终分解结果。

1.2灰色关联分析

灰色关联分析（greyrelationalanalysis，GRA）用于分析不同序列之间的相关性。在实际应用中，灰色关联度作为GRA的典型参数进行计算，通过灰色关联度的比较，可以评价不同因子序列对目标序列的影响程度［10］。要计算的样本序列可以表示为

si=（si（1），si（2），si（3），…，si（n），…，si（N））（1）

式中：i表示不同序列，当i=0时，s0表示目标序列；当i≠0时，si表示不同因子序列，n表示序列中的元素。

对原始序列进行极性统一和平均，使序列具有可比性，得到的相应序列标记为s（0）i和s（1）i：

s（0）i（n）=si（n）+|min（si（n））|（2）

s（1）i（n）=s（0）i（n）1N∑Nn=1s（0）i（n）（3）

式中：s（0）i（n）和s（1）i（n）分别表示相应序列s（0）i和s（1）i中的第n个元素。

计算目标序列s0与因子序列si之间的灰色关联系数γi（n）：

γi（n）=（miniminn|s（1）0（n）－s（1）i（n）|+

ρmaximaxn|s（1）0（n）－s（1）i（n）|）/

（|s（1）0（n）－s（1）i（n）|+

ρmaximaxn|s（1）0（n）－s（1）i（n）|）（4）

式中：ρ表示分辨系数，ρ∈［0，1］，较小的分辨系数意味着区分度更大。

由此可以进一步得到目标序列s0与因子序列si之间的灰色关联度ξi：

ξi=1N∑Nn=1ωγi（n）（5）

式中：ω表示权重系数，通常ω=1。

1.3互信息

互信息是信息学中的一个概念，可以用来度量两个随机变量共享的信息量，从而能够度量多个随机变量的相似程度。互信息是通过一个随机变量的已知信息来减少另外一个变量的不确定性［11］。设X、Y分别为χ、γ空间的离散随机变量，则X和Y的互信息I（X;Y）定义如下：

I（X;Y）=H（X）－H（X|Y）（6）

式中：H（X）、H（X|Y）表示信息熵及条件熵。其定义如下：

H（X）=－∑x∈χp（x）logp（x）（7）

H（X|Y）=－∑x∈χ∑y∈γp（x，y）logp（x|y）（8）

式中：p（x）为X的概率密度函数；p（x，y）为X和Y的联合概率密度函数；p（x|y）为条件概率密度函数。

信息熵和条件熵是用来衡量不同随机变量的不确定性的指标。互信息I（X;Y）是通过计算二者之差得出，互信息越大，二者之间相关性越强，反之则越弱，I（X;Y）=0则意味两个随机变量是相互独立的。

1.4谱峭度

谱峭度概念最早由DWYER［12］提出，他将峭度应用于短时傅里叶变换中，并引入频域峭度的概念。SK是一种衡量频域信号中的非高斯成分并确定其所处频带的方法。ANTONI［3］进行了细致研究，选择用四阶谱积累量来明确定义谱峭度，同时还提出了一种快速的谱峭度计算方法，以准确地确定冲击部分所在的最大频带和带宽［13］。在非平稳信号的Wold-Cramer分解中，可以将任何非平稳信号X（t）与其激励系统响应Y（t）之间的关系表示为

Y（t）=∫+∞－∞ej2πftH（t，f）dX（f）（9）

式中：H（t，f）为信号Y（t）在频率f处的复包络。

在条件非平稳（CNS）过程中的四阶谱积累量可以表示为

C4Y（f）=S4Y（f）－2S22Y（f），f≠0（10）

式中：S2nY（f）为包络H（t，f）的2n阶瞬时矩，用于复包络能量的衡量，其定义如下：

S2nY（f）=E{|H（t，f）dX（f）|2n}/df=E{|H（t，f）|2n}·S2nX（11）

因此，谱峭度被定义为能量归一化积累量，即概率密度函数的峰值度量。则可以得到谱峭度的定义如下：

KY（f）=C4Y（f）S22Y（f）=S4Y（f）S22Y（f）－2，f≠0（12）

滚动轴承故障信号模型可用式（13）定义：

Z（t）=X（t）+N（t）（13）

式中：Z（t）为实际测量振动信号；N（t）为加性平稳噪声。

根据式（12）对谱峭度的理论解释，Z（t）的谱峭度可以定义为

KZ（f）=KX（f）［1+ρ（f）］2，f≠0（14）

式中：KX（f）为X（t）的谱峭度；ρ（f）为噪信比，其定义为

ρ（f）=S2N（f）/S2X（f）（15）

式中：S2N（f）、S2X（f）分别为噪声和信号的功率谱密度。

由式（14）可知，在信号具有很高噪信比（噪声很强烈）的频带上KZ（f）趋近于0；而具有很低噪信比的地方，KZ（f）≈KX（f）。通过计算完整频域的谱峭度，能够找到具有最大谱峭度的频带，这个频带就是信号X（t）所处的频带。

2FMD滤波特性研究

为了说明FMD能够有效适用于实际工程中的非平稳信号，同时为了研究FMD中两个重要的输入参数（模态个数n和滤波器长度L）对其分解结果的影响，对其滤波特性进行研究是很有必要的。因此，本文借鉴基于分数阶高斯噪声（fractionalGaussiannoise，FGN）的数值模拟实验［14］分析FMD的滤波特性。FGN可以被视为离散时间序列的一种，并通过分数布朗运动（fractionalBrownmotion，FBM）表示，设xH（n）为一个FGN序列，则其自相关函数可以表示为

pH（l）=σ22（|l－1|2H－2|l|2H+|l+1|2H）（16）

式中：σ表示该时间序列的标准差；H为影响函数统计特性的指标。

首先，随机生成50组独立的FGN样本序列，每个样本序列包含2048个数据点，设置不同的Hrust指数（即H指数），标准差σ=0.1；其次，用FMD将每组样本序列分解为n个模态分量，计算分解后每个模态分量的功率谱；最后，计算50组样本序列各个模态的功率谱平均值，并以此作为数值模拟的输出结果。

设定FMD的模态个数n=6，滤波器长度L=16，研究不同H指数（H=0.2、H=0.5、H=0.8）的FMD的滤波特性，结果如图2所示，当H<0.5或H>0.5时，各模态分量平均功率谱幅值自右向左减小或增大，这体现了FGN随着Hrust指数变化而呈现的长趋势依赖性。当H=0.5时，FMD得到的各模态分量平均功率谱幅值有所差异，但其滤波特性基本一致，表现为与VMD相似的等效带通滤波器组的滤波特性。

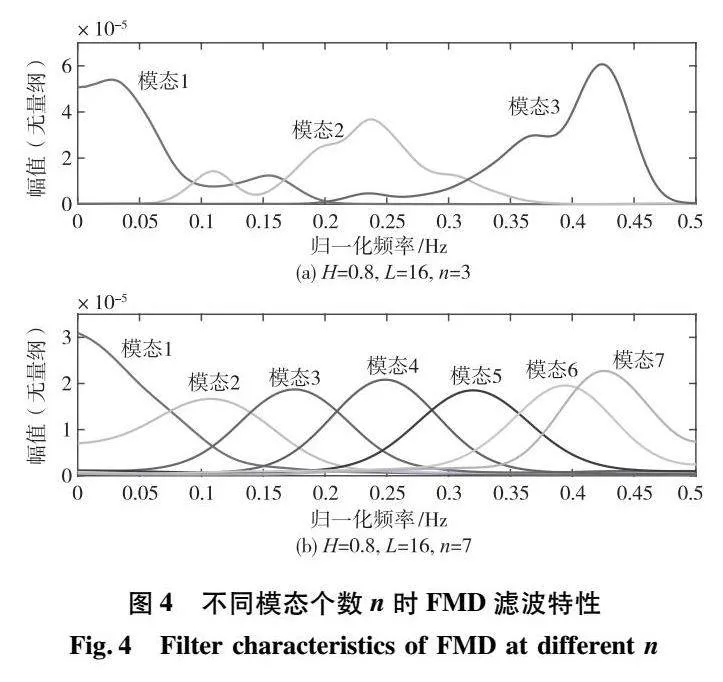
为了进一步研究FMD中不同输入参数对其滤波特性的影响，设定当H=0.5时，分别改变滤波器长度L和分解模态个数n来进行数值模拟实验分析。当模态个数n一定时，不同滤波器长度L对FMD滤波特性的影响如图3所示，当L过短时会导致各个模态的带宽过大，而L过长则会出现明显的通带波纹，均不利于信号的分解。当滤波器长度L一定时，不同模态个数n对FMD的滤波特性影响如图4所示，当n过少时，滤波器带宽较大且产生了明显通带波纹，不利于信号的降噪分解，但是n要满足n≤K，其中K为FIR滤波器初始化时划分的频带段数，数值模拟实验结果初步表明n=K-1时有较好的分解效果。

最后，本文选择FMD中模态个数n=6，滤波器长度L=16，采用汉宁窗初始化FIR滤波器，这样能够保证对多成分复杂信号的充分分解，能够在一定程度避免模态混淆，同时保证分解后各模态有合适的通带带宽并且不会出现明显通带波纹。

3特征提取方法

FMD能够同时考虑信号的脉冲性和周期性，分解目标以机械故障为导向，对其他的干扰具有鲁棒性，同时能够在没有故障周期作为先验知识的情况下有效分解复合故障信号［15］。但是FMD在分解之后存在多个模态，而其中包含若干虚假模态分量，无法准确选择故障特征所在模态。基于此问题，对FMD提出改进：首先，对信号用FMD得到若干模态分量；然后，采用灰色关联度和互信息来度量各个模态和原始信号之间的相关程度，从而选择相关性最强的模态分量作为最佳模态分量。由于谱峭度在轴承故障诊断研究中能够取得较好的诊断效果，故根据快速谱峭度计算方法得到信号分量的快速峭度图，并从中得到滤波所需的带宽和频带等参数，然后通过带通滤波进一步突出信号中的故障冲击部分，以便于提取故障特征频率。改进FMD和谱峭度结合的故障特征提取方法流程如图5所示。

4仿真信号分析

为了验证本文所提方法的有效性，采用式（17）模型来模拟轴承故障时的振动信号［16］。

x（t）=b（t）+r（t）+h（t）+n（t）

b（t）=∑iAie－950f0（tf0－i－τ）×

sin（4900πf0（tf0－i－τ））

r（t）=∑2j=12e－700（t－εj）sin（9000π（t－εj））

h（t）=0.3sin146πt+π6+0.3×

sin340πt－π3+0.6（0.5+0.3sin（15πt））（17）

式中：仿真信号由4部分信号组成；b（t）为震荡衰减函数模拟的轴承故障周期性脉冲信号；r（t）为外部冲击引起的随机脉冲信号，也用震荡衰减函数来进行模拟；h（t）由3个正弦分量组成，用于模拟转轴的低频谐波干扰信号；n（t）为轴承运行过程中标准差为σ的背景高斯白噪声。在b（t）中，Ai表示第i个故障脉冲的振幅且服从均匀分布U∈［0.9，1］；f0=100Hz为模拟故障频率；τ表示由均匀分布U∈［－0.02，0.02］产生的随机变量，用于模拟速度轻微波动引起的时间抖动。在r（t）中，j表示随机脉冲的个数；εj表示第j个随机脉冲出现的时间。高斯白噪声标准差σ=0933（信噪比SNR约为-15.60dB）。

轴承故障仿真信号采样频率fs=25600Hz，采样时间1s，图6为仿真信号时域图和频谱图。由于随机脉冲、离散谐波和强背景噪声的干扰，在图6（e）的轴承故障仿真信号中故障周期性脉冲成分无法直接观察到，如图6（f）所示，在f=2450Hz的周期脉冲共振频带可以观察到故障频率，而在低频带由于包含有强烈的低频离散谐波干扰和强背景噪声，无法识别频谱图中低频带的故障频率。

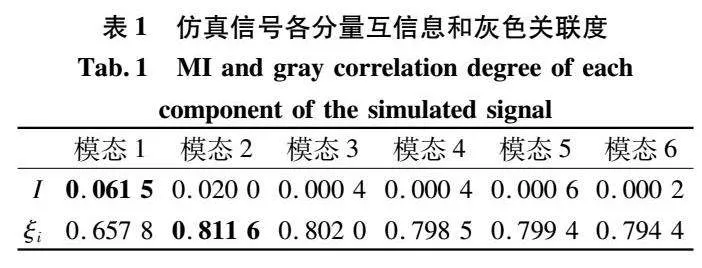
首先选择前文得到的输入参数n、L，采用该参数下的FMD对轴承故障仿真信号进行分解，得到6个模态分量。计算各个模态分量与原始信号之间的灰色关联度ξi和互信息I，以它们的结果来度量二者之间的相关性，计算结果如表1所示。

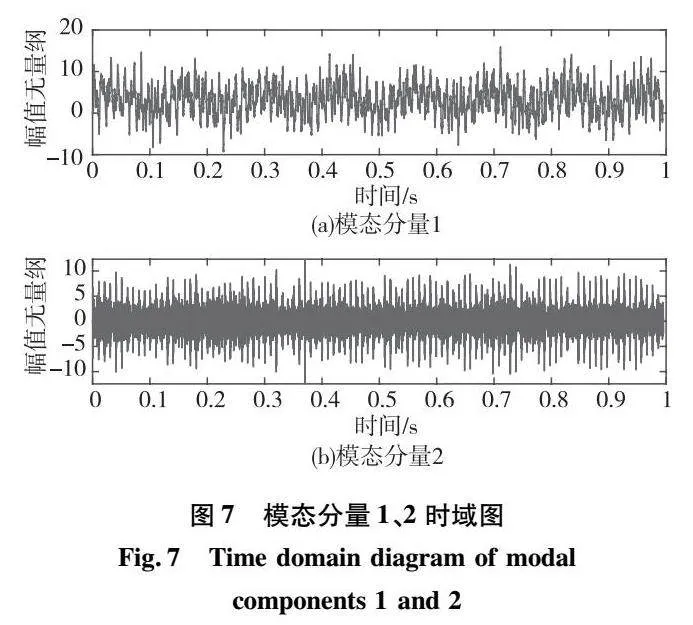
从互信息结果来看，模态分量1与原始信号的相关性最强，而模态分量2的灰色关联度最大，模态分量1、2的时域图如图7所示。根据时域图可以看出模态分量1为原信号中的低频谐波成分，模态分量2包含较多的周期性脉冲成分，这样可以看出该参数下的FMD能够对复杂的故障信号进行充分的分解，最后综合考量选择模态分量2为最佳模态分量。

根据谱峭度分析计算得到模态分量2的快速峭度图，如图8所示。从图中可以看出，最大峭度位于3200Hz，带宽为6400Hz，因此选取该参数构建的带通滤波器对最佳模态分量进行滤波和包络谱分析。

图9中，图9（b）为本文方法得到的仿真信号故障分析结果，为了进一步验证本文方法有效性，采用VMD进行对比分析，其惩罚因子默认为α=1000，模态个数为6来保证比较的公平性。从图9（b）中可以看出，本文提出方法包络谱中仿真信号故障频率f0=100Hz以及2f0～6f0在包络谱中谱线清晰可见，说明能有效提取到低频带的故障信息。而图9（a）中对最佳模态分量直接进行包络调解分析无法从包络谱中有效提取到故障特征频率，这说明了谱峭度方法的必要性。图9（c）为VMD的处理结果，从图中看出，VMD方法能够提取到故障频率，但是谱线并不突出，说明其提取效果不如本文提出方法。

从轴承故障仿真信号的对比结果可以看出，改进方法能够有效提取非平稳、包含噪声和脉冲干扰的轴承故障复合信号中的故障特征频率，对于噪声和其他干扰具有一定的鲁棒性，并比原包络谱和VMD方法有更好的提取效果。

5实验分析

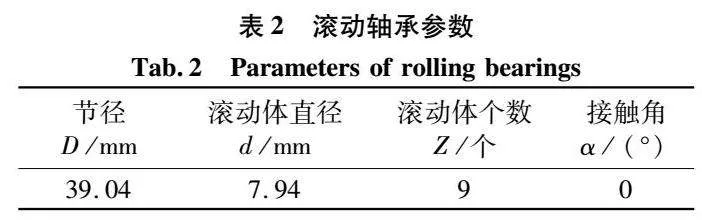
为了进一步验证改进方法的有效性，采用凯斯西储大学实际轴承故障实验数据来进行处理，实验平台如图10所示，其中实验用到的SKF6205-2RS轴承结构参数如表2所示。

利用电火花加工来产生轴承的单点故障，其中选择故障尺寸为0.1778mm，转速在1797r/min下的实验数据，采样频率为12000Hz，内圈轴承故障时域图如图11所示，为了对本文方法进行验证，对轴承内圈故障信号进行包络调解得到其包络谱如图13（a）所示。其中，式（18）用于计算轴承内圈理论故障频率：

f0=Zfr（1+dDcosα）2（18）

式中：fr为转频，计算得fr=29.95Hz，通过计算得出内圈理论故障频率f0=162.19Hz。

首先对轴承内圈故障信号通过FMD得到6个模态分量，然后对6个模态分量进行与原始信号互信息和灰色关联度的计算，结果如表3所示。

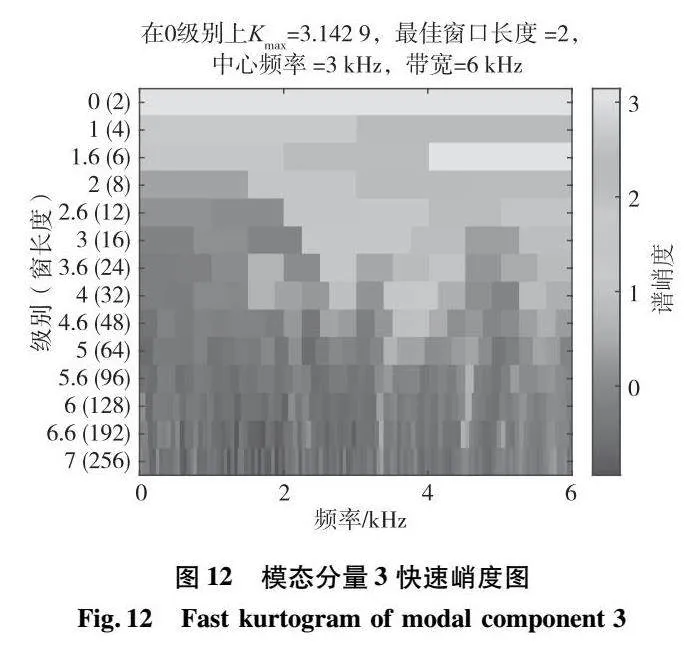
从表3可以看出，模态3的互信息和灰色关联度均最大，因此认为分解得到的模态3与原故障信号的相关程度最大，包含最多故障信息，所以选择模态3作为最佳模态进行进一步分析。对模态3进行谱峭度分析，得到其快速峭度图如图12所示。

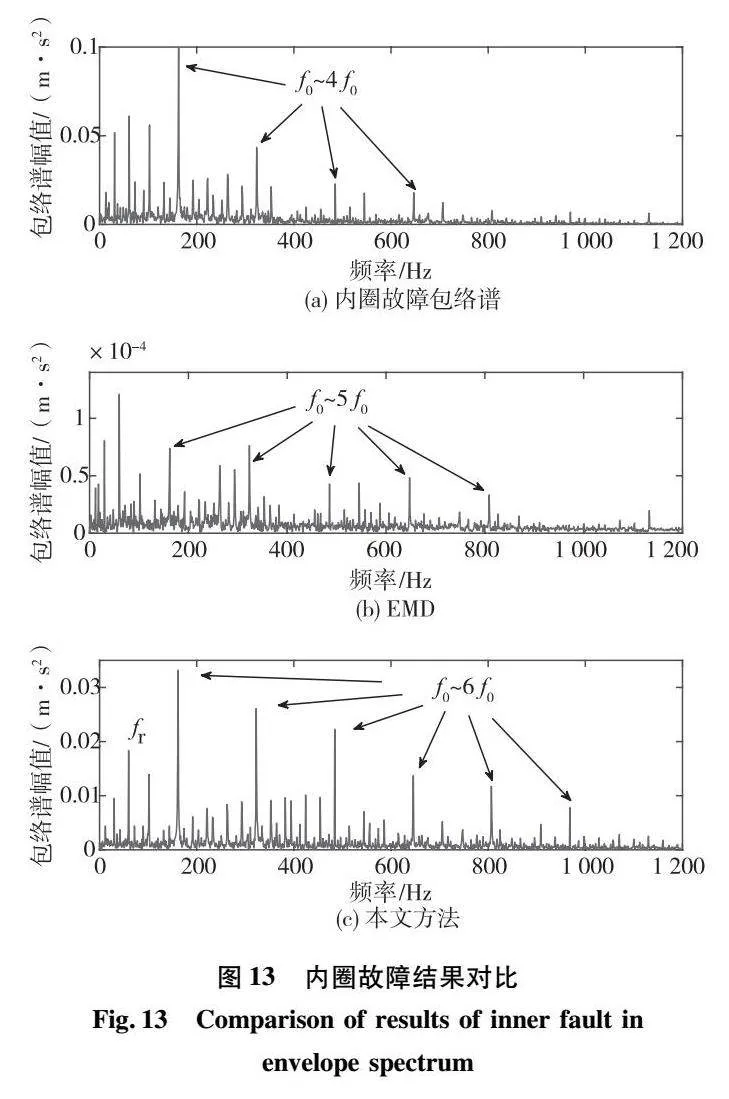
从图12可以看出，最大峭度中心频率位于3000Hz，带宽为6000Hz，峭度在整个频带上都较大，因此采用［10，5950］Hz的带通滤波器进行滤波处理，通过谱峭度分析后的最终结果如图13（c）所示。图13（a）中对轴承内圈故障直接进行包络分析能看到f0～3f0的谱线，但在低频部分包含严重的干扰成分，而在高频分段则几乎无法有效提取到故障特征。图13（b）中EMD的处理结果虽然能够突出高频带的故障频率，但是也放大了干扰频率的谱线。而本文方法在有效提取故障频率及倍频部分的同时，降低了转频fr及其他成分的干扰。

从轴承内圈故障的实验数据分析结果中可以看出，改进方法能够有效在分解模态中筛选出与原故障信号相关性最强的分量，并从中提取到了内圈故障频率f0=162Hz及其倍频成分，符合实际情况。并通过与传统包络调解分析方法和EMD方法的对比，可以看出本文所提方法对故障特征提取的效果更加明显。

6结论

1）基于分数阶高斯噪声数值模拟实验对FMD的带通滤波器组结构的滤波特性进行了研究，得到了FMD中两个重要输入参数（模态个数n和滤波器长度L）以及窗函数选择对FMD滤波特性的影响结果。为后续FMD在故障诊断领域中的研究提供了重要参考，同时也为FMD的参数自适应提供了思路。

2）针对FMD无法准确找到真实模态分量的问题，提出了用互信息和灰色关联分析来度量分解后各模态分量与原信号之间的相关性的改进FMD方法，该方法能有效地从多个模态中筛选最佳模态分量。

3）采用改进FMD结合谱峭度的特征提取方法，首先得到最佳模态分量，然后利用谱峭度方法对强背景噪声中的冲击成分进行有效定位，并经过带通滤波来凸显故障冲击成分，通过轴承故障仿真信号和真实轴承故障实验数据验证了本文所提方法的有效性，并且其效果优于传统包络调解方法，具有一定的工程应用价值，后续可以将它与一些模型（支持向量机、神经网络等）结合来实现轴承故障诊断。

参考文献：[1]KOUL，LIY，ZHANGFF，etal.Reviewonmonitoring，operationandmaintenanceofsmartoffshorewindfarms［J］.Sensors，2022，22（8）：2822.1-2822.36.

［2］HUANGWG，LISJ，FUXY，etal.Transientextractionbasedonminimaxconcaveregularizedsparserepresentationforgearfaultdiagnosis［J/OL］.Measurement，2020（2020-02-01）［2023-10-16］.https：//doi.org/10.1016/j.measurement.2019.107273.

［3］ANTONIJ.Thespectralkurtosis：ausefultoolforcharacterisingnon-stationarysignals［J］.MechanicalSystemsandSignalProcessing，2006，20（2）：282-307.

［4］CHENGY，ZHOUN，ZHANGWH，etal.Applicationofanimprovedminimumentropydeconvolutionmethodforrailwayrollingelementbearingfaultdiagnosis［J］.JournalofSoundandVibration，2018，425：53-69.

［5］MIAOYH，ZHAOM，LINJ，etal.Applicationofanimprovedmaximumcorrelatedkurtosisdeconvolutionmethodforfaultdiagnosisofrollingelementbearings［J］.MechanicalSystemsandSignalProcessing，2017，92：173-195.

［6］HUANGNE，SHENZ，LONGSR，etal.TheempiricalmodedecompositionandtheHilbertspectrumfornonlinearandnon-stationarytimeseriesanalysis［J］.ProceedingsoftheRoyalSocietyofLondonSeriesA，1998，454（1971）：903-995.

［7］LIANGT，LUH，SUNHX.Applicationofparameteroptimizedvariationalmodedecompositionmethodinfaultfeatureextractionofrollingbearing［J］.Entropy，2021，23（5）：520.

［8］DRAGOMIRETSKIYK，ZOSSOD.Variationalmodedecomposition［J］.IEEETransactionsonSignalProcessing，2014，62（3）：531-544.

［9］MIAOYH，ZHANGBY，LICH，etal.Featuremodedecomposition：newdecompositiontheoryforrotatingmachineryfaultdiagnosis［J］.IEEETransactionsonIndustrialElectronics，2023，70（2）：1949-1960.

［10］JIAYC，LIGL，DONGX.FeatureextractionofhobvibrationsignalsusingdenoisingmethodcombiningVMDandgreyrelationalanalysis［J］.ArabianJournalforScienceandEngineering，2021，47（3）：2925-2942.

［11］张平.基于多标签的特征选择算法研究［D］.长春：吉林大学，2021.

［12］DWYERR.Detectionofnon-Gaussiansignalsbyfrequencydomainkurtosisestimation［C］//TheICASSP1983IEEEInternationalConferenceonAcoustics，Speech，andSignalProcessing.Boston：IEEE，1983，8：607-610.

［13］ANTONIJ.Fastcomputationofthekurtogramforthedetectionoftransientfaults［J］.MechanicalSystemsandSignalProcessing，2007，21（1）：108-124.

［14］唐贵基，王晓龙.变分模态分解方法及其在滚动轴承早期故障诊断中的应用［J］.振动工程学报，2016，29（4）：638-648.

［15］YANXA，JIAMP.Bearingfaultdiagnosisviaaparameter-optimizedfeaturemodedecomposition［J/OL］.Measurement，2022（2022-11-15）［2023-10-16］.https：//doi.org/10.1016/j.measurement.2022.112016.

［16］CHENGY，WANGSB，CHENBY，etal.Animprovedenvelopespectrumviacandidatefaultfrequencyoptimization-gramforbearingfaultdiagnosis［J/OL］.JournalofSoundandVibration，2022（2022-04-14）［2023-10-16］.https：//doi.org/10.1016/j.jsv.2022.116746.

（责任编辑：曾晶）

Abstract：

Consideringthatthefaultsignalsofrollingbearingsusuallyexhibitnon-stationarycharacteristics，areeasilydisturbedandcannotbeeffectivelydiagnosed，animprovedfeaturemodedecomposition（FMD）combinedwithspectralkurtosis（SK）isproposedtoextractfaultfeaturesofrollingbearings.First，westudyedthefilteringcharacteristicsofFMDtoselecttwoimportantinputparametersreasonably;then，weusedFMDtoprocesstherollingbearingfaultsignaltoobtainthedecompositionresultsofmultiplemodalcomponents，andcalculatedtherelationshipbetweeneachcomponentandtheoriginalsignalbythegrayrelationaldegreeandmutualinformationtoselectthebestmodalcomponent;finally，wecombinedwithspectralkurtosis，bandpassfilteringisperformedonthebestmodalcomponenttoemphasizetheimpactcomponentwithinthesignal，therebyenablingextractionofthecharacteristicfaultfrequency.Byanalyzingthesimulationsignalandexperimentaldata，Itisfoundthattheproposedmethodcaneffectivelyextractthepeakenvelopespectrumandharmonicsofthefaultsignalcharacteristicfrequency，andthespectrallinefeaturesaremoreobviouscomparedtoothermethods，indicatingthatusingthismethodtodiagnosefaultsinrollingbearingsisfeasible.

Keywords：

featuremodedecomposition;spectralkurtosis;grayrelationalanalysis;rollingbearing;faultdiagnosis

收稿日期：2023-11-27

基金项目：福建省自然科学基金资助项目（2022J011169）

作者简介：张磊（1999—），男，在读硕士，研究方向：风电机状态监测与故障诊断，E-mail：1804825064@qq.com.

*通讯作者：陈学军，E-mail：cxjnet@126.com.