K-means++聚类算法研究与实现

摘要：聚类分析作为数据挖掘领域的一个关键研究热点，主要涉及数据分组技术。K-means算法作为一种经典的聚类方法，由于其简洁性和高效率而被广泛应用。然而，该算法存在一些明显的缺陷，如聚类中心的随机选择和较慢的收敛速度。文章在分析传统聚类算法的基础上，对K-means++算法进行了深入探讨。K-means++算法的核心思想是在选定后续聚类中心时，综合考虑当前已有聚类中心的分布，从而减少中心点的重叠。实验结果表明，K-means++通过选择更为分散的聚类中心，有效提高了聚类的准确性和算法的收敛速度，在改善聚类效率和精度方面具有显著优势。

关键词：聚类算法；K-means；K-means++；数据挖掘

中图分类号：TP311 文献标识码：A

文章编号：1009-3044（2024）17-0078-04 开放科学（资源服务）标识码（OSID） ：

0 引言

聚类是一种关键的无监督学习方法，用于将相似数据点分类并探索数据的内在结构[1]。通过揭示数据集中的密集和稀疏区域，聚类分析帮助研究人员识别全局分布模式和复杂数据属性关联，这不仅有助于理解数据的基本结构，还能在市场细分、社会网络和生物信息学等领域中发挥重要作用。作为数据预处理步骤，聚类通过特征提取和分类操作，提高了数据分析的精确度和效率。在处理大规模数据集时，这种方法可简化数据结构并明确研究方向。聚类算法在统计学、模式识别、计算几何、生物信息学、优化及图像处理等多个领域得到广泛应用，并在过去十年中取得了显著进展。

K-means聚类算法是数据挖掘领域中极受欢迎的一种算法。尽管由于其简单和高效而广泛应用，但该算法存在一些明显的局限性，如聚类中心的随机选择和较慢的收敛速度。为应对这些问题，改进版的K-means++算法应运而生，并成为本研究的焦点。Kmeans++通过更精细的初始聚类中心选择方法优化了标准K-means 算法，减少了算法收敛所需的迭代次数，并提高了聚类的最终质量。本文将详细探讨Kmeans++算法的原理、实现和优势，并通过实验验证其在实际应用中相较于传统K-means算法的改进效果。

1 聚类分析

聚类算法通过将数据实例分组，形成一系列被称为“簇”的相似组合。在这些簇内，数据实例通常在特征上表现出高度的相似性，而不同簇之间的数据实例则呈现出显著的差异。通过定义合适的距离度量或相似性系数，可以有效量化数据之间的相似性，从而实现数据的精确分类。

聚类不仅促进了数据的自动分类，还能将相似的数据集中处理，这对许多数据分析任务而言至关重要。本文主要研究利用聚类算法的这一功能，探索其在自动分类和数据分组中的应用效果，尤其聚焦于提升算法性能和数据处理效率方面的潜力。

1.1 聚类分析方法

划分方法是聚类分析中的一项核心技术，通过创建互斥的簇确保每个数据对象唯一地属于一个簇。这种方法主要基于距离度量，并且在开始之前需确定簇的数量k。初始划分完成后，划分方法采用迭代的重定位技术进行优化，即通过将数据对象从一个簇移动到另一个簇来改进分组效果。优化目标是确保簇内对象在特征上尽可能相似，而簇间对象尽可能不同，从而达到清晰的分类目的。这种方法不仅简化了数据结构，还增强了数据处理的有效性，使其能够在多种应用场景中提供有力支持。

划分聚类方法在对数据进行分组的同时进行分区，以提升数据管理和分析的效率。常见的划分聚类算法包括K-means、K-Medoids和K-Modes，各自适用于不同类型的数据和需求。

K-means：作为最广泛使用的划分聚类算法之一，适用于处理大规模数据集。该算法通过最小化簇内距离之和来优化簇的质心位置，适合处理连续数据。

K-Medoids：类似于K-means，但在选择簇中心时使用数据中实际存在的点（即medoids） ，增强了对异常值的鲁棒性，适合减少异常值影响的应用场景。

K-Modes：专为分类数据设计，使用模式（即数据中最频繁出现的点）而非平均值来定义簇中心，通过最小化不匹配的类别属性来形成簇，适合处理分类属性的数据集。

这些算法的效果依赖于预先定义的簇数量k，正确选择k值对于实现良好的聚类效果至关重要。通过这些方法，可以有效地将数据分为具有内部相似性和外部差异性的多个组或簇，从而使数据分析更加精确和高效。

1.2 K-Means 聚类算法

K-Means算法通过迭代计算簇中心的平均位置来重新定位这些中心，其经典算法流程包括以下步骤：

步骤1：初始化。算法从数据集中随机抽取k个数据点作为初始的聚类中心[2]。

步骤2：分配数据点。对于数据集中的每个点，根据其与各个聚类中心之间的距离进行分类。距离的度量方式可以根据数据的性质选择，例如欧氏距离、曼哈顿距离或余弦相似性。每个数据点被分配到最近的聚类中心所在的簇中。

步骤3：更新簇中心。完成数据点的分配后，下一步是更新每个簇的中心。使用欧氏距离时，新的簇中心是该簇内所有点的坐标平均值；若使用曼哈顿距离，则选择各维度的中位数；对于余弦相似性度量，则更新为簇内点的方向均值。

步骤4：迭代优化。算法重复执行分配和更新步骤，直至聚类中心的位置稳定下来或达到预定的迭代次数，这标志着算法已经收敛。

这个过程的核心目标是最小化簇内距离总和，从而优化簇中心的位置。K-Means算法以其简洁和高效性而被广泛应用于多种数据聚类任务，尽管它对初始中心选择敏感且可能陷入局部最优。

1.3 K-Means 聚类算法优缺点

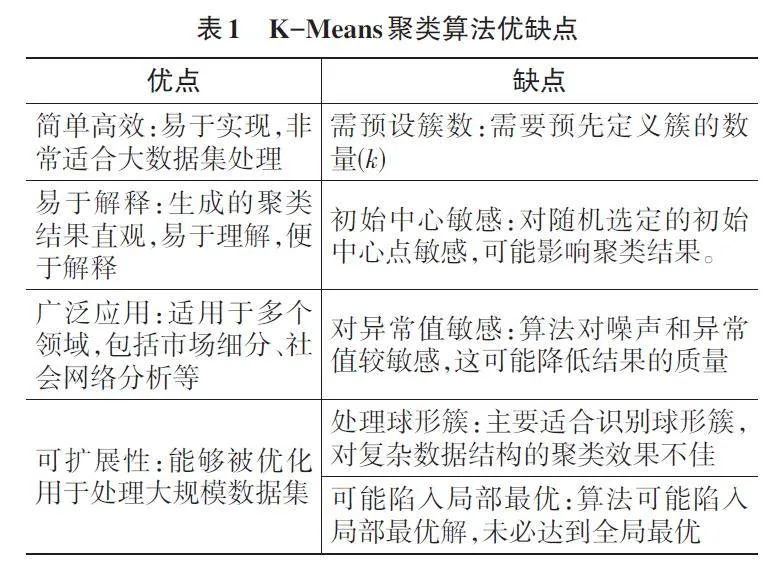
K-means是一种广泛使用的聚类方法，具有以下显著优点和一些限制[3]，如表1所示。

尽管K-means算法存在这些局限性，但通过适当的预处理和算法改进（如采用K-means++等方法），可以有效缓解这些问题，从而提高其在实际应用中的有效性。

2 K-means++聚类算法

2.1 K-means++聚类思想

K-means++的核心思想在于改进了初始化过程，通过更精细的策略选择初始聚类中心，以解决传统K-means算法中因随机初始化可能导致的聚类结果不稳定和质量不高的问题。

逐步选择聚类中心：

第一步：K-means++首先采用随机方法从数据集中选择一个点作为第一个聚类中心[4]。

后续步骤：对于选择后续聚类中心，算法计算每个尚未选为中心的点被选择为新中心的概率，这个概率与点到已选中心点的距离平方成正比。

这种方法显著减少了算法对随机初始聚类中心的依赖，降低了陷入局部最优解的风险，并能有效提高聚类的质量。此外，它也减少了算法运行时的迭代次数，从而提高了整体的效率和性能。

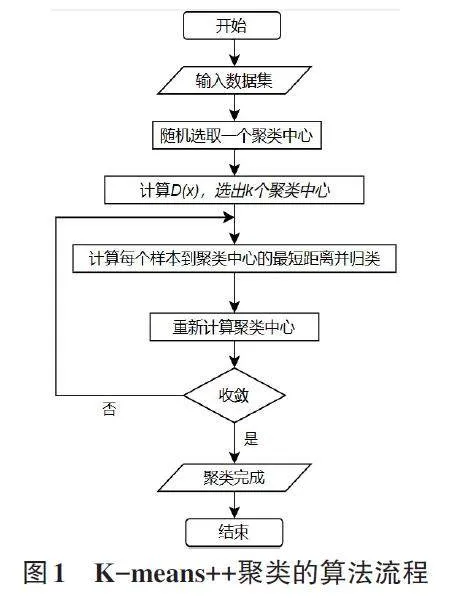
2.2 K-means++算法流程

K-means++聚类的算法流程如图1所示。

3 实验与分析

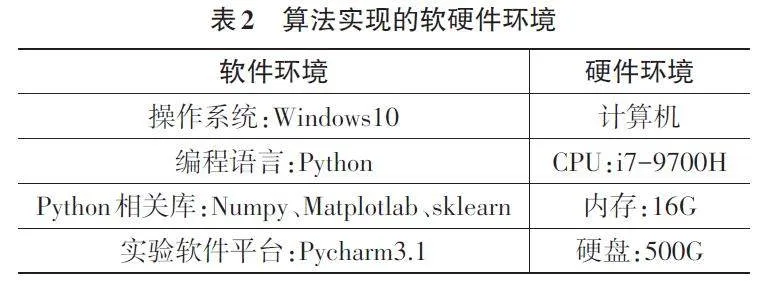
3.1 实验环境

本算法实现与测试的软硬件环境如表2所示。

3.2 实验数据

本文的实验数据来自sklearn 机器学习库中的make_blobs（）函数自动模拟生成，make_blobs（）函数常被用来生成聚类算法的测试数据，直观地说，make_blobs 会根据用户指定的特征数量、中心点数量、范围等来生成几类数据，这些数据可用于测试聚类算法的效果[5]。

#导入产生模型数据的方法

From sklearn.dataset import make_blobs

K=5 #确定聚类数量

X，Y= make_blobs（n_samples=5000，n_features=2，centers=k，random_state=1）

其中，n_samples是待生成的样本的总数，n_fea⁃tures是每个样本的特征数，centers表示类别数，clus⁃ter_state 表示每个类别的方差。当希望生成2 类数据，其中一类比另一类具有更大的方差，可以将clus⁃ter_std设置为[1.0，3.0]，10组样例数据如图2所示。

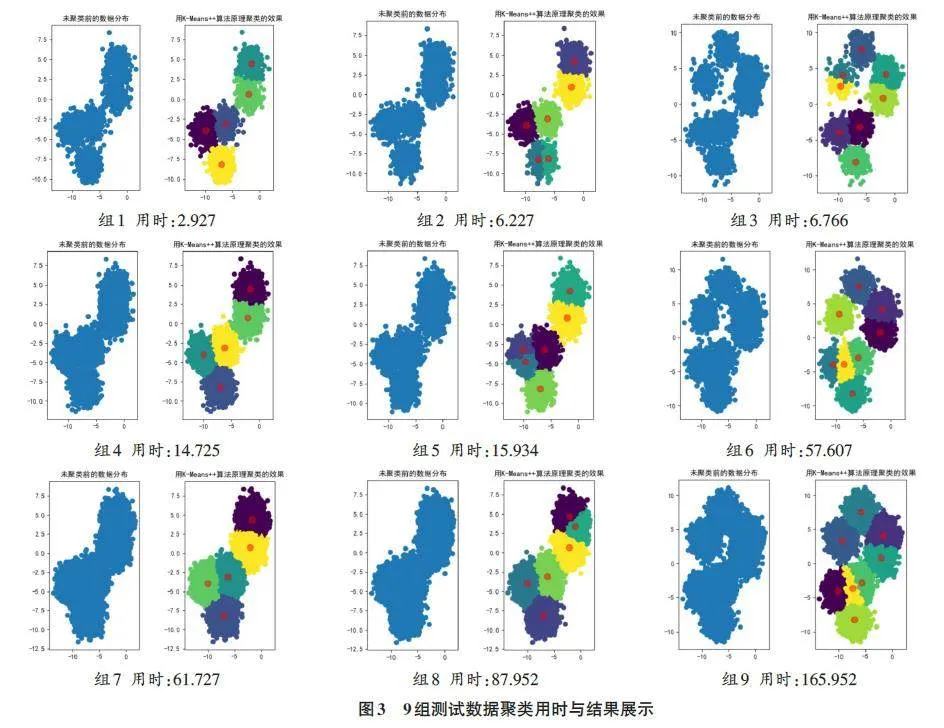
3.3 实验测试及结果

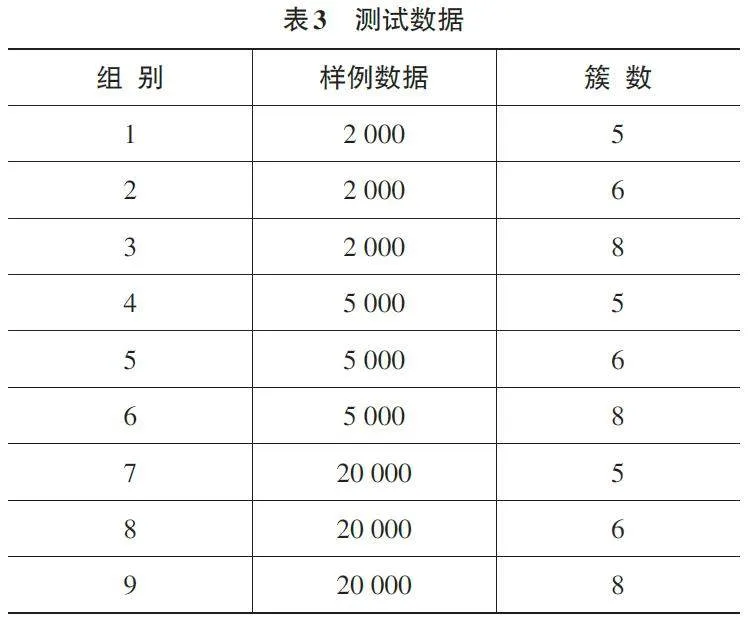
分别使用2 000、5 000、20 000三个不同数量的测试数据和划分为5、8、10三种簇共9个实验组来测试K-means++聚类算法的效果，为更清晰地展现实验测试数据，现将实验测试数据列表如表3所示。各组对应的聚类处理前后对比如图3所示，其中聚类用时保留小数点后3位，用时单位秒。

观察结果表明，K-means++算法不仅提高了聚类的效率，而且通过优化初始聚类中心的选择，提升了聚类结果的质量。

为了探究不同初始数据对K-means++算法的聚类效果，将make_blobs（）中的参数random_state作为变量，测试该算法的聚类效果。

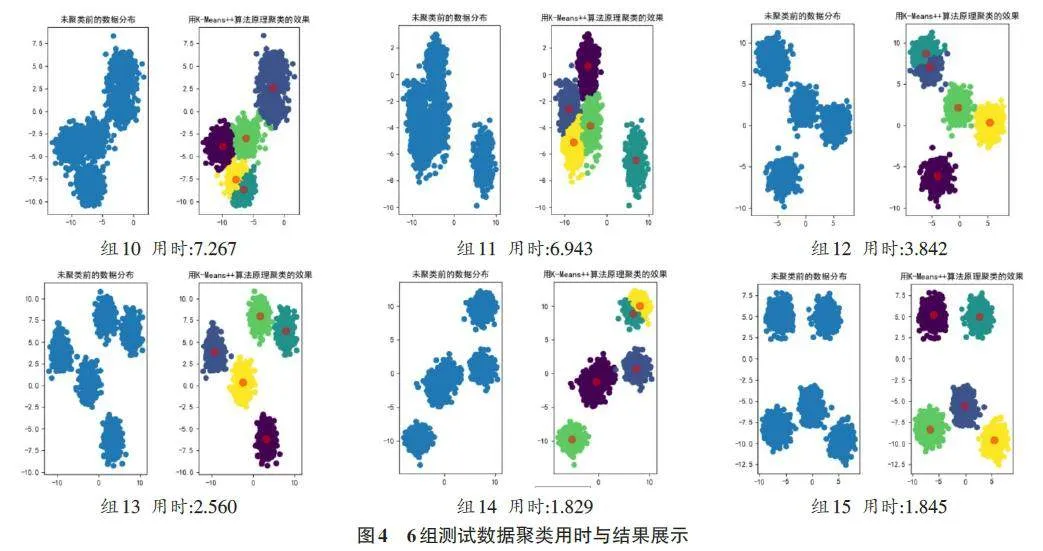
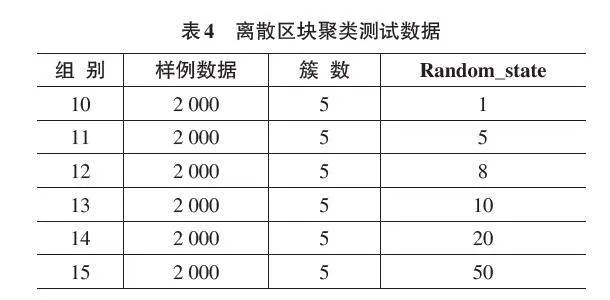
做出实验数据测试表如表4所示，实验结果如图4 所示，其中聚类用时保留小数点后3 位，用时单位秒。

从分析的6组图表结果来看，初始数据的特性对K-means++算法的运行时间产生显著影响。具体来说，当random_state参数较小，即各类别内的数据方差较小时，簇内数据点更加紧密，这使得K-means++算法需要更长的时间来进行聚类。相反，随着ran⁃dom_state参数的增大，即每个类别的方差增加，数据点更加分散，算法的运行时间相应减少。

这一现象的原因在于K-means++算法的核心步骤之一是计算每个点到所有聚类中心的距离，以确定数据点的簇归属。当数据点相对集中时，这些距离较小且差异不显著，因此算法需要进行更精细的操作来区分细微的距离差异，以实现簇的优化分割。而当数据点较为分散时，算法在初次迭代后就更容易形成明确的簇边界，这有助于减少迭代次数，从而加快收敛速度。

4 结论

综上所述，对初始数据进行适当的预处理是确保K-means++聚类算法成功应用及最大化效率和效果的关键。这一方法论在数据科学领域的各个方面均有广泛应用，且对提升算法性能有直接且显著的贡献。

参考文献：

[1] 李博.基于聚类分析的强化学习方法研究[D].成都：电子科技大学，2020.

[2] 李砚君.酒类电商精准营销研究[D].深圳：深圳大学，2017.

[3] 李伟，黄鹤鸣，张会云，等.基于深度多特征融合的CNNs图像分类算法[J].计算机仿真，2022，39（2）：322-326.

[4] 傅彦铭，李振铎. 基于拉普拉斯机制的差分隐私保护kmeans++聚类算法研究[J].信息网络安全，2019（2）：43-52.

[5] 孙立炜，王梦仙，黄泽.一种基于Logistic回归分析的药物筛选方法[J].科技资讯，2020，18（23）：214-216.

【通联编辑：谢媛媛】

基金项目：第五期江苏省职业教育教学改革研究课题：五年制高职创新创业教育课程体系构建的实践研究（以江苏联合职业技术学院扬州分院为例）（项目编号：ZYB376）