黑龙江省樟子松人工林林分直径结构模型的建立

王维芳 董继扬 张楚彤

摘 要 樟子松是中国北方的主要造林树种之一，具有抗寒、抗旱和环境适应性较强等优点。以樟子松人工林为研究对象，采用佳木斯市孟家岗林场6块不同龄组的固定样地数据，分析了樟子松人工林直径分布规律，建立了径阶和累积株数之间的关系模型，通过各种指标以及置信椭圆F检验进行了模型的检验。结果表明：（1）相同立地条件下，樟子松人工林的直径符合正态分布，接近平均直径处的林木株数最多，向两侧逐渐减少。（2）逻辑斯蒂方程可以较好拟合直径分布规律，各样地相关指数R2都大于0.99，实测数据基本都分布在拟合曲线附近。（3）拟合模型通过0.05显著水平下的F检验，林木的累积株数实测值和预测值之间的差异不显著，模型拟合效果较好，具有良好的合理性和适用性。

关键词 樟子松人工林；直径结构；模型拟合；逻辑斯蒂方程

中图分类号：S791.253.06    文献标识码：A   doi：10.13601/j.issn.1005-5215.2024.04.002

Establishment of Stand Diameter Structure Model of Pinus sylvestris var. mongolica Plantations in Heilongjiang Province

Wang Weifang1，Dong Jiyang2，Zhang Chutong3

（College of Forestry，Northeast Forestry University，Harbin 150040，China）

Abstract Pinus sylvestris var. mongolica is one of the main afforestation species in northern China，which has the advantages of cold resistance，drought resistance and strong environmental adaptability. Taking Pinus sylvestris var. mongolica plantations as the research objects，the diameter distribution law of Pinus sylvestris var. mongolica plantations was analyzed by using the data of six fixed sample plots of different age groups in Mengjiagang Forest Farm of Jiamusi City. The relationship model between diameter class and cumulative number of plants was established，and the model was tested by various test indexes and confidence ellipse F test. The results showed as the following three aspects. （1） Under the same site conditions，the diameter of Pinus sylvestris var. mongolica plantations conformed to the normal distribution. The number of trees near the average diameter was the largest，which gradually decreased to both sides. （2） The logistic equation can better fit the diameter distribution law，and the correlation index R2 of each plot was greater than 0.99，and the measured data were basically distributed near the fitting curve. （3） Through the F test at the significant level of 0.05，the fitting model showed no significant difference between the measured value and predicted value of the cumulative number of trees，and   the fitting effect of the model was good with good rationality and applicability.

Key words Pinus sylvestris var. mongolica plantations; diameter structure; model fit; logistic equation

樟子松（Pinus sylvestris var.mongolica）是我国北方主要造林树种之一，具有许多的价值[1]。因为其具有抗寒、抗旱、耐瘠薄和适应性强等特点，在我国三北地区的防护林及固沙造林建设中被广泛应用。随着沙地樟子松林的不断生长，枯枝落叶也逐渐增多，可以有效减少风蚀，对防风阻沙及改善环境产生重要作用[2-4]。在三北地区大力引进推广樟子松，对丰富当地造林树种种类，增强林地生产力，尤其是提高防风固沙能力和防护林体系建设质量，促进森林可持续经营，完成稳定、持续、防护和效益兼得的防护林体系具有重要意义[5，6]。

林分的直径结构是林分系统最基础、最关键的部分之一，是各种直径的树木在林分中的分布情况[7]。林分直径易于计算，而且各径阶林木的分布情况也直接反映了林木的树高、树冠面积和材积等要素的变化规律，这些因子都成为林分研究的重点内容，为后来许多林木管理方法和技术制表研究奠定了理论依据[8]。因此，对林分直径结构的深入研究，对于林分调查、编制经营数表和经营管理具有十分重要的意义[9-11]。

本研究通过对佳木斯市孟家岗林场樟子松人工林的林分直径进行分析，建立直径分布模型，初步研究其林分的直径结构，以期为樟子松人工林地生产力的增强及其可持续经营和永续发展提供基本的理论依据。

1 材料与方法

1.1 研究区域概况

研究地点在黑龙江省佳木斯市孟家岗林场，位于桦南县东北方，距县城21 km。地理坐标是46°20′16″—6°30′50″N，130°32′42″—130°52′36″E。林场占地16 274 hm2，林业用地14 107 hm2，其中，林地占13 079 hm2，森林资源

总量1 412 740 m3。未成林造林面积1 000 hm2，无林地面积仅有16 hm2，非林业用地2 167 hm2。拥有80.4%的森林覆盖率。

1.2 研究数据来源

选择代表性的林分，设置6个大小为600 m2的固

定样地，使用罗盘仪、皮尺或测绳进行闭合导线测量，闭合差≤1/200。对样地内直径5 cm以上的树木进行调查，测定胸径（DBH）、树高（HT）、枝下高（HCB）、冠幅（CW）。各样地的主要调查因子见表1。

2 结果与分析

2.1 直径正态分布

以2 cm为径阶，分别固定样地统计林木在各径阶的株数分布情况，是否符合正态分布，进行0.05显著水平下的卡方检验，检验结果如表2所示。

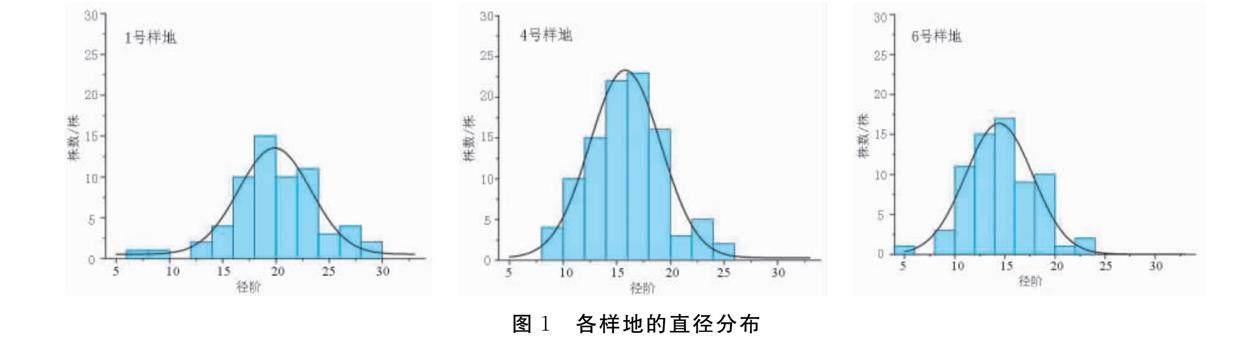
从表2中可以看出，6块固定样地检验的χ2值都小于相应的χ2临界值，实测株数与期望的理论株数之间没有太大的偏差。这说明正态分布的拟合效果较好。选取年龄不同的1号、4号和6号样地，作图描述林木株数和径阶的分布规律（图1）。

由图1可以知，1号样地的林木直径分布在8到30径阶，集中分布在20 cm径阶处。4号样地的林木直径分布在10到26径阶，集中分布在18 cm径阶处。6号样地的林木直径分布在6到24径阶，集中分布在16 cm径阶处，向两极逐渐减少，两侧大径阶和小径阶的林木株数相对较少，满足正态分布，说明相同立地条件、相同年龄的樟子松人工林的直径分布规律符合同龄林的直径结构的基本特点，即符合正态分布。

2.2 直径分布拟合2.2.1 逻辑斯蒂方程拟合

分别样地拟合理查德方程和逻辑斯蒂方程中的参数。逻辑斯蒂方程拟合结果较好，如表3所示。

6块固定样地的相关指数R2都大于0.99，最大的达0.999 5，最小的为0.998 2，说明了模型拟合很好。在6块固定样地中，6号样地拟合的相关指数（R2）最大，为0.999 5，其拟合效果最好；4号样地拟合的相关指数（R2）最小，为0.998 2，和其他样地相比，拟合效果相对较差，但也足以表明逻辑斯蒂方程可以很好地对式中各个参数进行估计。各个固定样地的参数P值都小于0.05，参数估计值都通过了0.05显著性水平下的t检验，说明了逻辑斯蒂方程可以很好地描述各样地的林木累积株数与林木径阶的关系。

2.2.2 模型精度检验

ME、MAE、MRE、MARE等检验指标的结果见表4。根据表4，各个样地ME都比较小，都小于0.2。从MAE看，都小于3.0。从MRE看，大部分样地都比较小，整体看模型预测比较合理。同时，F检验结果中，所有样地F值均小于相应F临界值，表明所有样地林木累积株数的实测值和预测值之间差异均不显著，说明此模型拟合效果较好。

3 结论与讨论

在相同立地条件下，樟子松人工林的直径分布状况符合正态分布，接近平均直径的林木株数较多，向两极逐渐减少。林木的径阶和累积株数之间的关系满足理查德方程和逻辑斯蒂方程的基本特征，其

中逻辑斯蒂方程效果更好，采用此方程进行模型拟合，各个样地的相关指数R2都大于0.99，说明对模型的拟合效果很好，各项检验指标值都比较小，整体看模型预测较为合理。另外，对模型进行0.05显著水平下的F检验，各个样地的F值均小于相应的F临界值，说明了逻辑斯蒂方程拟合效果较好，利用模型可以预估樟子松人工林的直径结构。如果能选择更多的样地进行连续调查，研究结果可能会更加明显合理。

参考文献：

[1] 李淑杰.樟子松人工林衰退原因及改造措施[J].安徽农学通报，2022，28（3）：79-83

[2] 许家春.樟子松人工林林分直径结构模式的研究[J].林业勘查设计，2019（2）：104-106

[3] 杨树军.樟子松人工林经营中存在的问题及可持续经营对策[J].农业开发与装备，2020（12）：228-229

[4] 翁同庆.关于异龄直径分布优化的研究[J].林业资源管理，1998，4（3）：49-53

[5] 吴承祯，洪伟.杉木人工林直径结构模型的研究[J].福建林学院学报，1998（2）：110-113

[6] 惠刚盈，盛炜彤.林分直径结构模型的研究[J].林业科学研究，1995，8（2）：127-131

[7] 曾德慧，姜凤岐.樟子松沙地人工林直径分布模拟[J].应用生态学报，1997，8（3）：231-234

[8] 王振亮，毕君.太行山刺槐人工林直径分布规律的研究[J].河北林业科技，1994（3）：15-18

[9] 杨凯，高燕平，李国春，等.红皮云杉人工林直径结构分布模型的研究[J].吉林林学院学报，1999，15（1）：14-19

[10] 李荣伟，唐志刚.杜仲人工林林分直径分布研究[J].四川林业科技，2000，21（2）：1-6

[11] 王艳洁，腾启和.河北省承德地区天然次生栋林直径分布的研究[J].林业资源管理，2001（1）：45-50

[12] 赵塔娜.内蒙古山地樟子松人工林林分结构及生长规律的研究[D].呼和浩特：内蒙古农业大学，2007

[13] 安慧君.阔叶红松林空间结构的研究[D].北京：北京林业大学，2003