结合模式性能和独立性加权的全球增暖1.5／2 ℃下中国区域气候的未来预估

周攀宇 江志红 李童

摘要 基于耦合模式比较计划第6阶段（CMIP6）中的全球气候模式的模拟结果，采用考虑模式性能和独立性结合（Climate model Weighting by Independence and Performance，ClimWIP）的加权方案进行中国区域气候的多模式集合预估及不确定性研究。结果表明，ClimWIP方案在历史阶段的模拟优于等权重方案，降低了多模式模拟的气候态偏差。温度指数的未来预估不确定性较大的区域主要集中在中国北方和青藏高原，而降水指数主要集中在华北和西北地区。ClimWIP方案的预估不确定性与等权重方案相比有所降低。ClimWIP方案预估的温度指数的增温大值区主要集中在中国北方和青藏高原;降水指数在西北和青藏高原增加最为显著。全球额外0.5 ℃增暖时，中国区域平均的温度指数变化更强，平均高于全球0.2 ℃，最低温在东北部分地区的额外增温甚至是全球平均的3倍;总降水额外增加5.2％;强降水额外增加10.5％。全球增暖2 ℃下，中国大部分区域温度指数较当前气候态增加可能超过1.5 ℃（概率>50％），在中国北方和青藏高原的部分地区增温超过1.5 ℃的可能性更大（概率>90％）;总降水，强降水和连续干日在西北和华北增加幅度有可能超过10％、25％和-5 d（概率>50％）。

关键词模式性能和独立性;全球增暖1.5／2 ℃;预估不确定性;概率预估;CMIP6

全球增暖背景下自然生态系统和人类社会将面临更大的挑战。2011—2020年全球地表温度较1850—1900年升高了1.09 ℃，并且在21世纪将持续上升，在高排放共享社会经济路径下，预计21世纪末全球气温升高约4.4（3.3～5.7） ℃（IPCC，2021）。随着全球变暖，高温热浪、强降水事件频发，强度更强，更易引发严重的气象灾害（Aslam et al.，2017;Guirguis et al.，2018;Sun et al.，2019;江晓菲等，2020;周波涛等，2020;孙雪榕等，2021;朱连华等，2023），对人类生命财产和国民经济建设造成严重损害。为应对气候变化的威胁，《巴黎协议》提出将全球平均气温升幅控制在较工业革命前2 ℃之内，并力争控制在1.5 ℃范围内（UNFCCC，2015）。众多研究表明中国区域的升温幅度和速率高于全球平均（胡婷等，2017;Shi et al.，2018），更容易受到极端气候事件的影响。因此进一步探索中国区域未来气候变化，给出更科学的未来预估具有重要意义。

全球气候模式（Global Climate Models，GCM）在气候模拟和未来气候变化预估方面发挥着重要作用。新一代气候模式对过去和当前气候模拟能力的提升，将增强未来预估的可靠性（Palmer et al.，2005;Semenov and Stratonovitch，2010）。世界气候研究计划（WCRP）已经组织了多次耦合模式比较计划（Coupled Model Intercomparison Projects，CMIP），旨在统一的框架下开展多模式比较，如今已经进行到第六阶段（CMIP6），参与第六阶段的模式比前一阶段模式（CMIP5）在参数化方案和模式分辨率等方面有了较大的改进和提高，已有大量研究证明CMIP6比CMIP5能够更好地模拟极端气候指数及其趋势变化特征（Zamani et al.，2020;Zhu et al.，2020;Li J J et al.，2021）。

气候系统内部的自然变率，模式本身分辨率和参数化方案的限制，以及未来情景的不确定性等方面，使得模式预估结果存在较大不确定性。多模式集合已被证明可以有效降低区域气候预估的模式间不确定性（Abramowitz and Bishop，2015;Sanderson et al.，2015）。简单模式集合平均已经被广泛用于未来气候预估并且证明可以得到比单个模式更优的模拟（Tebaldi and Knutti，2007;Knutti，2010;Knutti et al.，2010;蒋帅等，2017;Eyring et al.，2019）。但是，由于每个模式的模拟性能不同，同等对待每个模式已不再是最优方案（Baumberger，2017;Eyring et al.，2019）。基于模式性能的集合方案得到了进一步发展，例如，秩加权方案（Chen et al.，2011，Li et al.，2016）和可靠性集合平均方法（Giorgi and Mearns，2002，2003;朱欢欢等，2022）。随后有研究指出很多模式的设计不完全独立，因此有必要考虑模式间的相互依赖问题。Knutti et al.（2017）提出了一种考虑了模式性能和独立性的方案，该方案的应用区域多集中于欧洲，被证明可以提高模拟性能并有效降低未来预估的不确定性（Knutti et al.，2017;Brunner et al.，2019;Brunner et al.，2020a）。

目前使用该全面考虑模式性能和独立性的集合方案在中国区域的研究还较少，Zhao et al.（2022）基于该方案研究了青藏高原的降水变化，发现该方案预估的降水，在季节上，春季的降水增加趋势增强;在空间上，高原西北部是降水量增加的响应大值区。Li T et al.（2021）基于此方案进行了全球增暖1.5／2 ℃下中国区域降水与极端降水的预估，发现加权后预估的未来降水增幅总体更强，降水的局地响应更明显。该研究仅以105°E为界，将中国进行东西分区，并选择参数建模，考虑到中国区域气候差异大，仅东西分区无法兼顾模式在更为局地尺度上的性能差异，因此或许并不是最优的集合方案。故本文在已有研究的基础上，使用最新一代的CMIP6模式数据，进一步在更为细致的局地尺度进行多模式建模分析，对全球增暖1.5／2 ℃背景下中国区域的温度和降水进行集合预估，并进一步给出预估不确定性的分析及概率预估结果。

1 资料和方法

1.1 资料

本文使用的观测数据集为中国区域的格点日资料CN05.1，使用的变量为逐日平均、最高、最低气温和逐日降水量，关注的历史时间段为1961—2014年。该数据集是由吴佳和高学杰（2013）基于中国2 416个地面气象站的观测资料插值得到的分辨率为0.25°×0.25°的格点数据集。本文使用的模式资料为CMIP6模式资料，与观测资料使用了相同的变量，考虑了其历史模拟（1850—2014年）和未来SSP5-8.5情景（2015—2100年）的逐日数据，其中SSP5-8.5情景是共享社会经济路径（Shared Socio-economic Pathways，SSPs）下的高耗能发展排放情景（ONeill et al.，2016;Riahi et al.，2017）。根据以上条件筛选出了25个CMIP6模式资料，各模式信息如表1所示，本文仅使用每个模式的第一个集合成员。

1.2 气候指数

本文关注了6个气候指数，包括3个气温指数：年平均气温、日最低温年最小值（以下简写为最低温）和日最高温年最大值（以下简写为最高温），以及3个降水指数：年总降水、强降水量和连续干日。指数的定义源于气候变化检测和指标专家组定义（ExpertTeam on Climate Change Detection and Indices，ETCCDI）（http：／／etccdi.pacificclimate.org／），各指数具体信息如表2所示。由于各模式数据的空间分辨率不同，我们首先在观测和模式资料的原网格上计算各指数，后采用双线性插值的方法，将观测和模式资料计算得到的气候指数结果统一插值到1°×1°的网格点上，许多关于未来气候变化的相关研究也使用了这样的插值方案（Zhou et al.，2014;Yang et al.，2021;Zhu et al.，2021）。

1.3 方法

1.3.1 考虑模式性能和独立性的模式加权方案

本文使用的是由Knutti et al.（2017）提出的考虑模式性能和独立性加权方案（Climate model Weighting by Independence and Performance，ClimWIP）。它对模式的权重赋予遵循两个原则：1）与观测结果不一致的模式权重较小;2）重复现有模式结果的模式均分权重。

首先我们需要计算模式i与观测的“距离”Di，以及模式i和模式j之间的“距离”Sij。本文中“距离”主要基于各模式对温度和降水的空间模态以及年际变率的模拟评估，通过标准化的空间均方根误差（RMSE）和标准化的年际变率技能评分（Interannual Variability Skill，IVS）计算得到，本文利用模式的中值进行标准化。

空间均方根误差定义为：

其中：MK和OK分别表示模式与观测的气候态均值;N表示区域内空间点的个数。RMSE值越小，说明模式与观测的空间模态一致性越好。

对年际变率的模拟评估使用的是Chen et al.（2011）定义的技能评分IVS，该指标由模式与观测的时间序列年际标准差的相似程度确定，具体如下所示：

其中：STDm和STDo分别表示模式和观测的时间序列年际标准差。IVS值越小，说明模拟的年际变率与观测结果越接近。

以上关于RMSE和IVS描述以得到模式i与观测之间的“距离”Di为例，类似的，我们可以得到模式i与模式j之间的“距离”Sij。

接下来可以基于公式（3）计算得到模式i的权重wi：

其中：M是模式总数;参数σD和σS用于约束模式的性能和相似度。较大的σD使模式权重趋于相等，而较小的σD使得仅有少数模式得到较大权重;σS确定了一个模式与另一个模式相似的标准距离。确定参数σD和σS使用了交叉验证方法（Brunner et al.，2019），具体步骤如下：针对σD和σS，首先选择合适的范围区间（参照前人的研究，本文选择的范围区间为0.2～1.4）和迭代步长（0.02）;而后将对应的每一组σD和σS带入权重公式（3），利用交叉验证方法，将每个模式依次视为“伪观测”，利用其余模式进行模式集合，选择使得“伪观测”的预估值落在加权方案的5％～95％百分位数范围内的比例超过90％的最小的一组σD和σS作为最优参数。该参数优选步骤，在一定程度上可以确保加权模型应用于未来时段的适用性。该参数确定步骤和思想与已有文献类似（Lorenz et al.，2018;Brunner et al.，2019，2020b;Amos et al.，2020）。Brunner et al.（2019）的研究表明交叉验证方法在较小区域会选择更高的σD值，从而使权重更均匀地分布，来避免在格点尺度建模的过度拟合问题，为进一步考虑模式在更为局地尺度上的性能差异，我们选取了各格点上优选参数并确定权重的方案（以下简称ClimWIP_grid方案）。同时与Li T et al.（2021）采用的仅考虑中国东西部分区的建模方案（以下简称ClimWIP_we方案）进行对比。等权多模式集合方案（Multi-Model Ensemble，MME）也作为对比方案之一。

1.3.2 泰勒图

本文使用泰勒图（Taylor，2001）和泰勒技巧评分（Taylor Skill Score，TSS;Wang et al.，2018）来综合评估各方案对气候指数空间特征的模拟能力。泰勒图主要包括3个指标：相关系数、均方根误差和相对标准差。相关系数越大、均方根误差越小、相对标准差越接近于1，表明模拟结果与观测更为接近，模式模拟能力越强。泰勒技巧评分是泰勒图的定量化表示：

其中：Rm是模拟结果与观测的气候态空间场的相关系数;R0是此处可达到的最大相关系数，设为0.999;σm和σo分别是模拟和观测的气候态空间场的标准差。TSS值越接近1，模拟与观测的一致性越好。

1.3.3 未来预估的不确定性

本文利用“模式离差”来定量表示模式未来预估的不确定性（李博和周天军，2010），其定义为：

其中：N是模式数;wi是第i个模式的权重;Δxi是第i个模式预估的未来变化。模式离差越小，说明未来预估的不确定性越小。

1.3.4 给定阈值的概率预估

加权集合方案的给定阈值下的概率预估值P可以由超过该阈值的模式权重和表征，其数学表达式为：

其中：i代表模式;wi为该模式权重;ΔTth为设定的关注阈值;ΔTi为模式i的变化值。

1.3.5 全球增暖达到1.5 ℃和2 ℃的定义

模式到达1.5／2 ℃的时间段参考了以往的研究（Shi et al.，2018;Zhu et al.，2021），首先计算全球平均地表温度21 a滑动平均的时间序列，以此确定一个相对稳定的气候态，而后选择各个模式的全球增温首次达到相对于工业化前（1861—1900年）1.5／2 ℃的时间，取达到时间的前9 a和后10 a共20 a的时间段表征未来增暖1.5／2 ℃下的气候态。

2 结果

2.1 集合方案对气候指数历史气候态模拟能力的评估

首先，在历史阶段进行集合方案对中国当前气候指数的模拟能力的评估。图1给出了ClimWIP_grid、ClimWIP_we和MME三种方案模拟的验证期1995—2014年3个温度指数与观测场的绝对偏差空间分布及空间分布对应的箱线图。结果表明，ClimWIP_grid方案的模拟能力最优，其模拟偏差较原始模式集合显著更低。3种方案模拟的年平均气温（最低温）在中国大部分区域表现为冷偏差，冷偏差的大值区主要集中在青藏高原和四川盆地，MME方案的冷偏差最大值超过了4.5 ℃（9 ℃），ClimWIP_we方案在青藏高原的模拟较MME方案有明显改善，而ClimWIP_grid方案模拟效果最优，在全国范围的偏差都较小，即使在冷偏差最大的青藏高原和四川盆地地区，其值也没有超过2.5 ℃（5 ℃）。对于年最高温，3种方案在华北和西北地区存在暖偏差，在青藏高原和长江以南以冷偏差为主，ClimWIP_we方案和MME方案的偏差分布整体类似，ClimWIP_we方案在华北的偏差较小，而ClimWIP_grid方案在全国大部分地区的偏差都在0.5 ℃以下。整体来看，集合方案模拟的偏差大值区集中在西北和青藏高原地区。由对应箱线图发现，ClimWIP_grid方案对较大的冷偏差改善尤为明显，当关注第10百分位数时，MME方案对应平均气温、最低温和最高温的值分别为-3.47、-7.75和-2.45 ℃，而ClimWIP_grid方案模拟的偏差大小仅为-1.17、-2.47和-0.96 ℃，分别降低了2.3、5.28和1.49 ℃。

图2给出了3种集合方案模拟的1995—2014年总降水和强降水与观测场的相对偏差以及连续干日与观测场的绝对偏差空间分布及其对应的箱线图。从中国区域整体来看，总降水和强降水的偏差分布特征较为类似，降水指数以湿偏差为主，在青藏高原外围和新疆南部湿偏差最大;干偏差主要集中在准噶尔盆地和柴达木盆地，强降水在华南地区有约15％的干偏差。ClimWIP_we方案在青藏高原外围的湿偏差大值区范围比MME方案略有减少，而ClimWIP_grid方案显著减少了模拟的湿偏差大值区范围，总降水在除青藏高原外围的中国大部分地区湿偏差降至15％以下。对于连续干日，三种方案的偏差空间分布特征类似，ClimWIP_grid方案在青藏高原外围的湿偏差大值区范围相对较小。整体来看，ClimWIP_grid方案的模拟最优，对湿偏差大值的改善尤为明显。以第90百分位数为例，MME方案对应总降水、强降水和连续干日的偏差值分别为232％、314％和-78 d，而ClimWIP_grid方案仅为68％、126％和-48 d，分别降低了164％、188％和30 d。

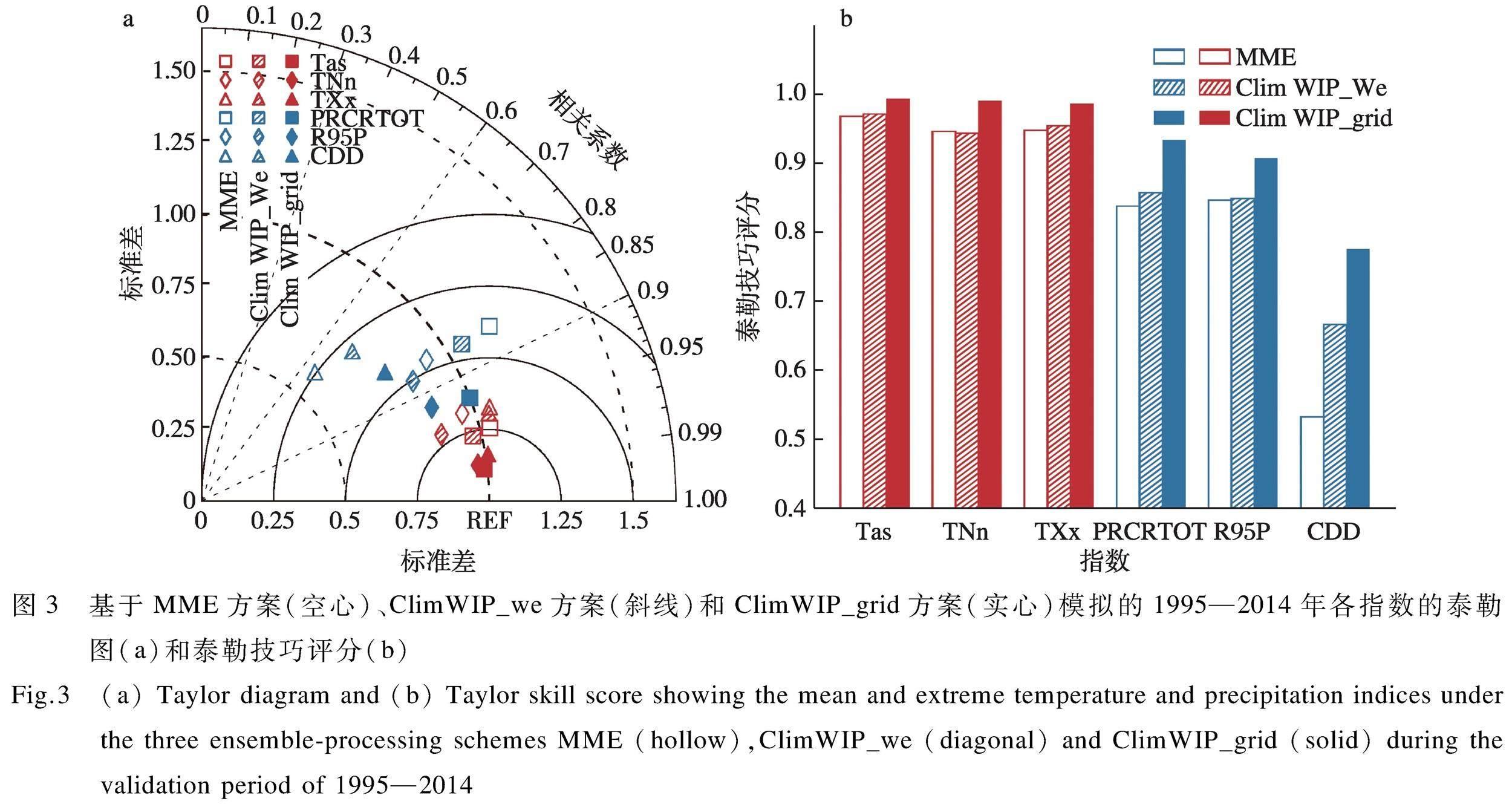
进一步利用泰勒图综合评估对比三种方案对气候指数空间特征的模拟能力。由图3a容易看出3种方案对温度指数的模拟都相对较好，空间相关系数均在0.95以上，能更好地再现温度指数的空间结构;对总降水和强降水空间结构的模拟比温度指数稍差，但相关系数也在0.85以上。其中ClimWIP_grid方案模拟最优，3个温度指数相关系数在0.98以上;相对标准差接近1，在空间变率方面的模拟与观测非常接近;均方根误差在0.15左右，与观测的偏差较小。降水指数除连续干日外的相关系数超过0.92，相对标准差在0.8～1.0之间，均方根误差在0.55～0.6之间。TSS指标（图3（b））也显示ClimWIP_grid方案最优，温度指数都在0.98以上，降水指数也比其他两种方案提高了至少0.1，总降水和强降水提高到了0.93和0.9。

从以上分析可知ClimWIP_grid方案在历史时期的模拟能力最优，因此接下来将ClimWIP_grid方案应用于全球增暖1.5／2 ℃下中国区域的未来预估。

2.2 未来预估

2.2.1 未来预估的不确定性

由于气候模式的未来预估存在模式间不确定性，ClimWIP_grid方案是否可以降低未来预估不确定性是我们关注的重点。图4和图5给出了SSP5-8.5情景下全球增暖1.5 ℃时，ClimWIP_grid方案和MME方案模拟的温度和降水指数离差的空间分布，以及两者离差的差异。

对于温度指数（图4），总的来看，温度指数在中国北方和青藏高原地区的离差相对较大，说明在这些地方不确定性较大;平均温度的离差低于最低温和最高温，说明极端温度的不确定性相对更大。ClimWIP_grid方案与MME方案相比，在全国大部分地区的离差都是减小的，平均温度、最低温和最高温的区域平均离差分别减小了20％、20.2％和12.1％。针对3个温度指数，离差减小较多的区域分别集中在中国长江以南地区、长江流域和青藏高原西部，降低幅度可达80％以上，总的来说温度指数在中国南方和青藏高原不确定性减小较多。

从图5可以看出，降水指数在华北和西北的离差较大，说明在该地区降水的预估不确定性较大。对比ClimWIP_grid方案与MME方案的预估不确定性差异，发现总降水和强降水的空间分布特征较为类似，ClimWIP_grid方案在中国大部分区域的离差都小于MME方案，总降水和强降水区域平均的离差分别减小了11.7％和12％，其中在东北和新疆西北部的离差减小更多，最多可超过80％;对于连续干日，ClimWIP_grid方案的预估不确定性相比MME方案整体改善不明显，仅在中国的东南部和新疆西北部的离差减小较大。

全球增暖2 ℃下的结论与增暖1.5 ℃类似（图略），但是整体离差大于增暖1.5 ℃时。全球增暖2 ℃时，与MME方案相比，ClimWIP_grid方案预估的平均气温、最低温和最高温区域平均离差分别降低了19.2％、22.1％和17.8％，总降水和强降水区域平均的离差分别降低了3.3％和4.7％。整体而言，ClimWIP_grid方案较MME方案可以降低未来预估不确定性。

2.2.2 未来预估空间分布

由上述分析可知，ClimWIP_grid方案对历史气候态的模拟是最优的，并且能够有效降低未来预估的不确定性，因此我们基于该方案，探究全球增暖1.5／2 ℃下我国的未来气候变化特征。图6给出了SSP5-8.5情景下全球增暖1.5、2 ℃和额外0.5 ℃增暖时，ClimWIP_grid方案预估的3个温度指数较历史参考期（1995—2014年）变化的空间分布。3个温度指数的增温变化在中国几乎所有区域都通过了置信度为95％的显著性检验，这表明未来增温较当前在统计意义上显著。基于ClimWIP_grid集合方案的预估显示，平均温度的未来增温在北方更强，在东北、华北和新疆北部的增温最明显;最低温的增温大值区集中在中国北方和青藏高原外围，全球增暖2 ℃下增幅最高超过2.5 ℃，而在四川盆地增温幅度最低;对于最高温，增温大值区主要集中在西北和青藏高原。全球增暖1.5 ℃（2 ℃）时，平均气温，最低温和最高温的中国区域平均变化为1.07、1.32和1.17 ℃（1.79、2.13和1.95 ℃）。额外的0.5 ℃增暖将使得3个温度指数的中国区域平均增温幅度都超过0.7 ℃，其中东北和西北增温最强，最低气温在东北部分地区增温甚至超过了1.5 ℃，是全球额外增暖幅度的3倍。

图7给出了SSP5-8.5情景下全球增暖1.5、2 ℃和额外0.5 ℃增暖时ClimWIP_grid方案预估的降水指数相较历史时期的变化，可以看出，总降水和强降水变化的空间分布较为类似，未来以降水增多为主，其大值区位于西北和青藏高原，两个指数的变化极大值分别超过了24％和48％;预估的总降水减少出现在东北部分地区和云南，强降水减少主要集中在东北地区。连续干日在长江以南的变化以增多为主，说明该地区未来降水将减少，其中在云南增加最多，极大值超过4 d;在长江以北区域以减少为主，在西北减少最多，最多减少超过16 d。全球增暖1.5 ℃（2 ℃）时，总降水、强降水和连续干日的全国区域平均变化为6.58％、22.04％和-2.94 d（11.75％、32.54％和-5.34 d）。全球增暖2 ℃时相较1.5 ℃，降水总体以增加为主，总降水和强降水的中国区域平均值分别增加了5.2％和10.5％，连续干日减少2.4 d，在青藏高原北部和新疆南部增加最明显，总降水和强降水增加分别超过16％和32％，连续干日减少高于8 d。

2.2.3 概率预估

由上述分析可知，不同区域之间的不确定性有明显差异，ClimWIP_grid方案可以减小未来预估的不确定性，为此，我们进一步给出ClimWIP_grid方案的中国区域气候指数的概率预估，结合上文未来预估空间分布的分析，针对各指数选择了不同的阈值。

图8和图9给出了在SSP5-8.5情景下全球增暖1.5／2 ℃时各指数超过对应阈值概率的空间分布。对于各温度指数，在1.5 ℃增暖背景下，我们关注的阈值为较当前（1995—2014年）增温1.0 ℃;在2 ℃增暖背景下，关注的阈值为较当前增温1.5 ℃。由图8很容易看出温度指数在全球增暖1.5和2 ℃超过对应阈值概率的空间分布特征相似，且增暖2 ℃时超过对应阈值的概率更高，这说明在额外的0.5 ℃增暖下，中国区域的增温更强。平均温度和最低温的概率分布特征相似，全球增暖1.5／2 ℃时长江以北的大部分区域的增幅都有可能超过1.0／1.5 ℃（概率>50％），其中在青藏高原东部的横断山脉附近以及华北部分地区增幅极有可能超过1.0／1.5 ℃（概率>90％）。最高温在除东北和华北以外的大部分区域增幅有可能超过1.0／1.5 ℃（概率>50％），在西北和青藏高原增温的可能性更大，其中部分区域概率大于90％。

对于降水指数，1.5／2 ℃增暖背景下，总降水关注阈值为0％、5％和10％，强降水的关注阈值为5％、15％和25％，连续干日的关注阈值为-1、-3和-5 d。由图9可知全球增暖2 ℃时，总降水在除云南外的地区都有可能增加（概率>50％），在西北、青藏高原和华北部分区域增加的可能性更高，概率超过了90％;当关注的阈值为较当前增加5％时，概率超过90％的区域明显减少;而阈值增加到10％时，仅西北、青藏高原和华北部分区域增加可能超过该阈值（概率>50％）。与之进行对比，强降水的增加更为显著，在几乎全国所有区域都可能增加超过5％（概率>50％）;当关注的阈值为15％时，除东北及秦岭附近区域外的其他地区有可能增加超过该阈值（概率>50％）;阈值增加到25％时，仅青藏高原和西北部分区域可能增加超过该阈值（概率>50％）。连续干日在长江以北可能减少（概率<50％），说明未来降水可能增加，在华北和西北部分地区减小的可能性更高，概率可以达到90％，阈值为-3 d时，概率超过90％的区域明显减少;而当关注阈值为-5 d时，仅西北和华北部分区域连续干日减少可能大于5 d（概率>50％）。总体来说，降水指数在西北和华北增加的概率更高。全球增暖1.5与2 ℃的分布特征相似，但是超过对应阈值的概率稍小，特别是在东北地区概率明显更小。

3 结论与讨论

本文基于25个CMIP6模式的模拟结果，采用考虑模式性能和独立性（ClimWIP）结合的加权方案进行了中国区域温度和降水指数的多模式集合预估，在历史阶段与已有的加权方案对比，并给出了中国区域气候指数未来预估的不确定性分析及概率预估结果，主要结论如下：

1）格点建模的ClimWIP_grid方案在历史时期的模拟较区域建模ClimWIP_we与等权重集合MME方案相比更优，其模拟的气温和降水指数的中国区域偏差最小，更好地模拟出了气温和降水指数的空间分布。

2）SSP5-8.5情景下全球增暖1.5／2 ℃时，温度指数在中国北方和青藏高原地区的预估不确定性相对较大，降水指数在华北和西北的不确定性较大。ClimWIP_grid方案的预估不确定性较MME方案有所降低，中国南方和青藏高原温度不确定性减小较多，降水则在东北和新疆西北部的不确定性减小明显。

3）基于ClimWIP_grid方案的预估结果，在全球增暖1.5／2 ℃时，平均气温的未来增温在东北、华北和新疆北部最明显;最低温的增温大值区集中在中国北方和青藏高原边缘地区;最高温的增温大值区集中在西北地区和青藏高原;极端气温的增温幅度大于平均气温。3个降水指数的变化大值区都在中国西北地区和青藏高原。额外0.5 ℃增暖下，中国区域平均的温度指数增温都将达到0.7 ℃及以上，其中东北和西北增温更强，最低温在东北部分地区增温甚至达到全球额外增暖的3倍以上;总降水的增加幅度为5.2％，强降水的增加幅度为10.5％。

4）全球增暖2 ℃下，中国大部分地区温度指数增温都可能超过1.5 ℃（概率>50％），在中国北方和青藏高原的部分地区增温超过1.5 ℃的可能性更大（概率>90％）;总降水，强降水和连续干日在西北和华北增加幅度有可能超过10％、25％和-5 d（概率>50％）。

值得注意的是，本文在建模时仅使用了每个模式的第一个集合成员，若利用模式的多集合成员可以进一步考量内部变率的作用。本研究使用的全球气候模式分辨率较低，对中国西部尤其是地形复杂地区的模拟较差，使用高分辨率的气候模式或者结合动力及统计降尺度技术有望改善在地形复杂区域的模拟，从而给出更为可靠的未来预估。

参考文献（References）

Abramowitz G，Bishop C H，2015.Climate model dependence and the ensemble dependence transformation of CMIP projections［J］.J Climate，28（6）：2332-2348.doi：10.1175／jcli-d-14-00364.1.

Amos M，Young P J，Hosking J S，et al.，2020.Projecting ozone hole recovery using an ensemble of chemistry-climate models weighted by model performance and independence［J］.Atmos Chem Phys，20（16）：9961-9977.doi：10.5194／acp-20-9961-2020.

Aslam A Q，Ahmad S R，Ahmad I，et al.，2017.Vulnerability and impact assessment of extreme climatic event：a case study of southern Punjab，Pakistan［J］.Sci Total Environ，580：468-481.doi：10.1016／j.scitotenv.2016.11.155.

Baumberger C，Knutti R，Hirsch Hadorn G，2017.Building confidence in climate model projections：an analysis of inferences from fit［J］.Wires Clim Change，8（3）：e454.doi：10.1002／wcc.454.

Brunner L，Lorenz R，Zumwald M，et al.，2019.Quantifying uncertainty in European climate projections using combined performance-independence weighting［J］.Environ Res Lett，14（12）：124010.doi：10.1088／1748-9326／ab492f.

Brunner L，McSweeney C，Ballinger A P，et al.，2020a.Comparing methods to constrain future European climate projections using a consistent framework［J］.J Climate，33（20）：8671-8692.doi：10.1175／jcli-d-19-0953.1.

Brunner L，Pendergrass A G，Lehner F，et al.，2020b.Reduced global warming from CMIP6 projections when weighting models by performance and independence［J］.Earth Syst Dynam，11（4）：995-1012.doi：10.5194／esd-11-995-2020.

Chen W L，Jiang Z H，Li L，2011.Probabilistic projections of climate change over China under the SRES A1B scenario using 28 AOGCMs［J］.J Climate，24（17）：4741-4756.doi：10.1175／2011jcli4102.1.

Eyring V，Cox P M，Flato G M，et al.，2019.Taking climate model evaluation to the next level［J］.Nat Clim Change，9：102-110.doi：10.1038／s41558-018-0355-y.

Giorgi F，Mearns L O，2002.Calculation of average，uncertainty range，and reliability of regional climate changes from AOGCM simulations via the “reliability ensemble averaging” （REA） method［J］.J Climate，15（10）：1141-1158.doi：10.1175／1520-0442（2002）015<1141：coaura>2.0.co;2.

Giorgi F，Mearns L O，2003.Probability of regional climate change based on the Reliability Ensemble Averaging （REA） method［J］.Geophys Res Lett，30（12）：1629.doi：10.1029／2003gl017130.

Guirguis K，Gershunov A，Cayan D R，et al.，2018.Heat wave probability in the changing climate of the Southwest US［J］.Climate Dyn，50（9）：3853-3864.doi：10.1007／s00382-017-3850-3.

IPCC，2021.Summary for Policymakers［M］／／Climate change 2021：the physical science basis.Cambridge：Cambridge University Press.

胡婷，孙颖，张学斌，2017.全球1.5和2 ℃温升时的气温和降水变化预估［J］.科学通报，62（26）：3098-3111. Hu T，Sun Y，Zhang X B，2017.Temperature and precipitation projection at 1.5 and 2 ℃ increase in global mean temperature［J］.Chin Sci Bull，62（26）：3098-3111.doi：10.1360／N972016-01234.（in Chinese）.

蒋帅，江志红，李伟，等，2017.CMIP5模式对中国极端气温及其变化趋势的模拟评估［J］.气候变化研究进展，13（1）：11-24. Jiang S，Jiang Z H，Li W，et al.，2017.Evaluation of the extreme temperature and its trend in China simulated by CMIP5 models［J］.Clim Change Res，13（1）：11-24.doi：10.12006／j.issn.1673-1719.2016.053.（in Chinese）.

江晓菲，江志红，李伟，2020.全球增温1.5和2 ℃下中国东部极端高温风险预估［J］.大气科学学报，43（6）：1056-1064. Jiang X F，Jiang Z H，Li W，2020.Risk estimation of extreme high temperature in Eastern China under 1.5 and 2 ℃ global warming［J］.Trans Atmos Sci，43（6）：1056-1064.doi：10.13878／j.cnki.dqkxxb.20201011001.（in Chinese）.

Knutti R，2010.The end of model democracy？［J］.Clim Change，102（3）：395-404.doi：10.1007／s10584-010-9800-2.

Knutti R，Furrer R，Tebaldi C，et al.，2010.Challenges in combining projections from multiple climate models［J］.J Climate，23（10）：2739-2758.doi：10.1175／2009jcli3361.1.

Knutti R，Sedlcˇek J，Sanderson B M，et al.，2017.A climate model projection weighting scheme accounting for performance and interdependence［J］.Geophys Res Lett，44（4）：1909-1918.doi：10.1002／2016GL072012.

Li J J，Huo R，Chen H，et al.，2021.Comparative assessment and future prediction using CMIP6 and CMIP5 for annual precipitation and extreme precipitation simulation［J］.Front Earth Sci，9：430.doi：10.3389／feart.2021.687976.

Li T，Jiang Z H，Zhao L L，et al.，2021.Multi-model ensemble projection of precipitation changes over China under global warming of 1.5 and 2 ℃ with consideration of model performance and independence［J］.J Meteorol Res，35（1）：184-197.doi：10.1007／s13351-021-0067-5.

Li W，Jiang Z H，Xu J J，et al.，2016.Extreme precipitation indices over China in CMIP5 models.part II：probabilistic projection［J］.J Climate，29（24）：8989-9004.doi：10.1175／jcli-d-16-0377.1.

Lorenz R，Herger N，Sedlcˇek J，et al.，2018.Prospects and caveats of weighting climate models for summer maximum temperature projections over North America［J］.J Gcophys Res：Atmos，123（9）：4509-4526.doi：10.1029／2017jd027992.

李博，周天军，2010.基于IPCC A1B情景的中国未来气候变化预估：多模式集合结果及其不确定性［J］.气候变化研究进展，6（4）：270-276. Li B，Zhou T J，2010.Projected climate change over China under SRES A1B scenario：multi-model ensemble and uncertainties［J］.Adv Clim Change Res，6（4）：270-276.doi：10.3969／j.issn.1673-1719.2010.04.007.（in Chinese）.

ONeill B C，Tebaldi C，van Vuuren D P，et al.，2016.The scenario model intercomparison project （ScenarioMIP） for CMIP6［J］.Geosci Model Dev，9（9）：3461-3482.doi：10.5194／gmd-9-3461-2016.

Palmer T N，Shutts G J，Hagedorn R，et al.，2005.Representing model uncertainty in weather and climate prediction［J］.Annu Rev Earth Planet Sci，33：163-193.doi：10.1146／annurev.earth.33.092203.122552.

Riahi K，van Vuuren D P，Kriegler E，et al.，2017.The shared socioeconomic pathways and their energy，land use，and greenhouse gas emissions implications：an overview［J］.Glob Environ Change，42：153-168.doi：10.1016／j.gloenvcha.2016.05.009.

Sanderson B M，Knutti R，Caldwell P，2015.Addressing interdependency in a multimodel ensemble by interpolation of model properties［J］.J Climate，28（13）：5150-5170.doi：10.1175／JCLI-D-14-00361.1.

Semenov M A，Stratonovitch P，2010.Use of multi-model ensembles from global climate models for assessment of climate change impacts［J］.Clim Res，41：1-14.doi：10.3354／cr00836.

Shi C，Jiang Z H，Chen W L，et al.，2018.Changes in temperature extremes over China under 1.5 ℃ and 2 ℃ global warming targets［J］.Adv Clim Change Res，9（2）：120-129.doi：10.1016／j.accre.2017.11.003.

Sun C X，Jiang Z H，Li W，et al.，2019.Changes in extreme temperature over China when global warming stabilized at 1.5 ℃ and 2.0 ℃［J］.Sci Rep，9（1）：14982.doi：10.1038／s41598-019-50036-z.

孙雪榕，葛非，罗浩林，等，2021.全球增暖1.5 ℃和2.0 ℃下成渝经济区及周边地区极端温度事件的变化预估［J］.大气科学学报，44（6）：875-887. Sun X R，Ge F，Luo H L，et al.，2021.Projected changes of temperature extremes in Chengdu-Chongqing Economic Zone and its surrounding areas under 1.5 ℃ and 2.0 ℃global warming［J］.Trans Atmos Sci，44（6）：875-887.doi：10.13878／j.cnki.dqkxxb.20201221001.（in Chinese）.

Taylor K E，2001.Summarizing multiple aspects of model performance in a single diagram［J］.J Geophys Res，106（D7）：7183-7192.doi：10.1029／2000jd900719.

Tebaldi C，Knutti R，2007.The use of the multi-model ensemble in probabilistic climate projections［J］.Philos Trans A Math Phys Eng Sci，365（1857）：2053-2075.doi：10.1098／rsta.2007.2076.

The United Nations Framework Convention on Climate Change （UNFCCC），2015.Adoption of the Paris Agreement［C］／／UNFCCC Conference of the Parties.

Wang B，Zheng L H，Liu D L，et al.，2018.Using multi-model ensembles of CMIP5 global climate models to reproduce observed monthly rainfall and temperature with machine learning methods in Australia［J］.Int J Climatol，38（13）：4891-4902.doi：10.1002／joc.5705.

吴佳，高学杰，2013.一套格点化的中国区域逐日观测资料及与其它资料的对比［J］.地球物理学报，56（4）：1102-1111. Wu J，Gao X J，2013.A gridded daily observation dataset over China region and comparison with the other datasets［J］.Chin J Geophys，56（4）：1102-1111.（in Chinese）.

Yang X L，Zhou B T，Xu Y，et al.，2021.CMIP6 evaluation and projection of temperature and precipitation over China［J］.Adv Atmos Sci，38（5）：817-830.doi：10.1007／s00376-021-0351-4.

Zamani Y，Hashemi Monfared S A，Azhdari moghaddam M，et al.，2020.A comparison of CMIP6 and CMIP5 projections for precipitation to observational data：The case of Northeastern Iran［J］.Theor Appl Climatol，142（3）：1613-1623.doi：10.1007／s00704-020-03406-x.

Zhao Y，Zhou T J，Zhang W X，et al.，2022.Change in precipitation over the Tibetan Plateau projected by weighted CMIP6 models［J］.Adv Atmos Sci，39（7）：1133-1150.doi：10.1007／s00376-022-1401-2.

Zhou B T，Wen Q H，Xu Y，et al.，2014.Projected changes in temperature and precipitation extremes in China by the CMIP5 multimodel ensembles［J］.J Clim，27（17）：6591-6611.doi：10.1175／jcli-d-13-00761.1.

周波涛，徐影，韩振宇，等，2020.“一带一路”区域未来气候变化预估［J］.大气科学学报，43（1）：255-264. Zhou B T，Xu Y，Han Z Y，et al.，2020.CMIP5 projected changes in mean and extreme climate in the Belt and Road region［J］.Trans Atmos Sci，43（1）：255-264.doi：10.13878／j.cnki.dqkxxb.20191125009.（in Chinese）.

Zhu H H，Jiang Z H，Li J，et al.，2020.Does CMIP6 inspire more confidence in simulating climate extremes over China？［J］.Adv Atmos Sci，37（10）：1119-1132.doi：10.1007／s00376-020-9289-1.

Zhu H H，Jiang Z H，Li L，2021.Projection of climate extremes in China，an incremental exercise from CMIP5 to CMIP6［J］.Sci Bull，66（24）：2528-2537.doi：10.1016／j.scib.2021.07.026.

朱欢欢，姜胜，江志红，2022.基于可靠性集合平均方法的全球1.5／2.0 ℃变暖下中国极端气候的未来预估［J］.地球科学进展，37（6）：612-626. Zhu H H，Jiang S，Jiang Z H，2022.Projection of climate extremes over China in response to 1.5／2.0 ℃ global warming based on the reliability ensemble averaging［J］.Adv Earth Sci，37（6）：612-626.（in Chinese）.

朱连华，祝颖锜，姚壹壹，等，2023.全球增暖1.5／2 ℃下中国区域极端降水的风险变化及其影响因子［J］.大气科学学报，46（1）：97-109. Zhu L H，Zhu Y Q，Yao Y Y，et al.，2023.Risk and impact analysis of extreme precipitation over China under 1.5 and 2℃global warming levels［J］.Trans Atmos Sci，46（1）：97-109.doi：10.13878／j.cnki.dqkxxb.20210811002.（in Chinese）.