聚焦基础知识 考查关键能力
廖国达

2024年高考数学新课标I卷(简称“新课标I卷”)聚焦基础知识的夯实,通过优化题量、提升解答题分值和多选题赋分的方式,旨在更好地体现数学的本质,强化对学生理性思维和应用能力的考查。改革后的新课标I卷旨在培养学生的核心素养,选拔具备创新精神的优秀人才。试卷呈现出选择和填空题整体难度适中、试题梯度设计合理、解答题具有一定的难度和区分度等特点。试卷着重考查学生的主干知识、能力和素养,突出思维过程、思维方法和创新能力,助力素质教育和拔尖人才的选拔,充分体现了改革的理念和要求。
重视基础,回归课标,突出数学教学本质
1.重点考查主干知识
从具体的考查内容来看,这份试卷重点考查主干知识,具体包括:函数与导数(第6、8、10、13、18题,共38分)、解析几何(第11、12、16题,共26分)、立体几何(第5、17题,共20分)、三角函数(第4、7、15题,共23分)、概率统计(第9、14题,共11分)、数列(第19题,17分)、集合(第1题,5分)、复数(第2题,5分)以及向量(第3题,5分)。
值得注意的是,虽然平时常考的知识点,如直线与圆、等比数列、二项式定理、统计、回归方程、分布列等并未直接出现在试卷中,但不等式作为解决数学问题的重要工具,被巧妙地融入了多个考题(第1、6、8、9、10、11、18题)之中,体现了其作为一条暗线的核心作用。这样的设计不仅考查了学生对基础知识的掌握,也检验了他们的解题技巧和灵活应用能力。
2.考查基础知识,回归教材
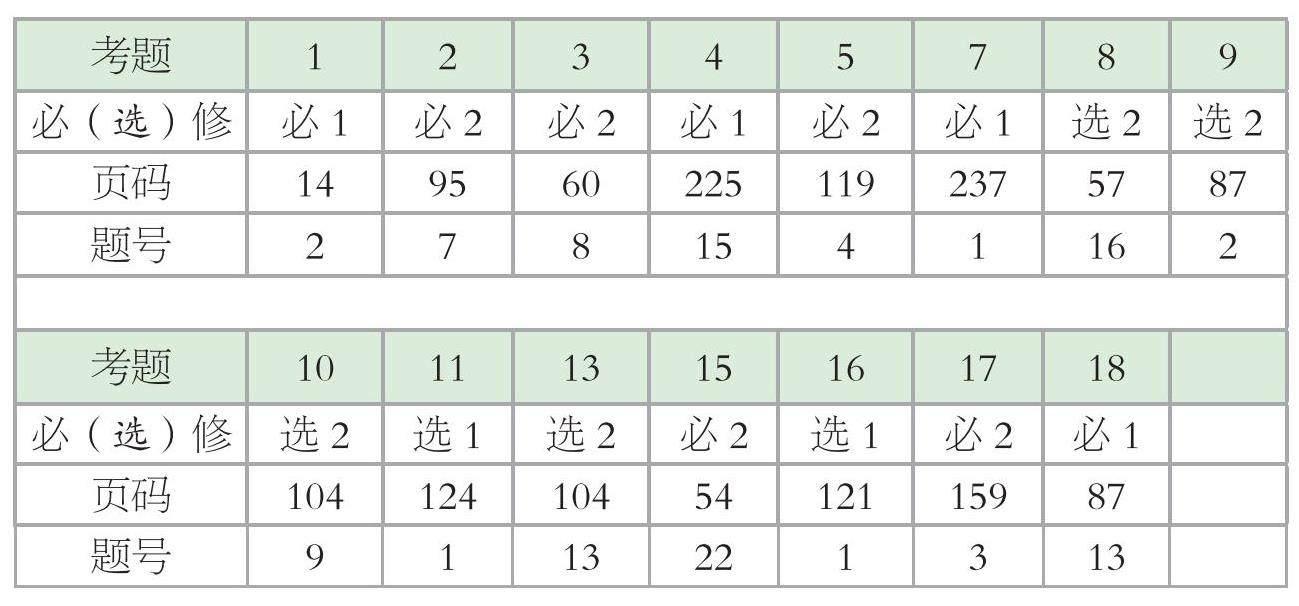
仔细审视试卷内容,可以发现其仍然以考查基础内容为主导,多数题目的题源都可以追溯到人民教育出版社出版的《普通高中教科书数学》(2019年6月第1版),如下表所示:
从考试内容中我们可以明显看出,对数学基础知识和基本概念的理解是考查的重点,大部分考题都源于课本上的例题或习题中的常规题型。因此,对2025届高三学生来说,坚持掌握和巩固基础知识体系显得尤为重要。考生应当多加练习课本上的例题和习题,以深化对知识点的理解和运用。
重点考查学生的关键能力
1.试卷的灵活性有所提高,重视理性思维
第8题:已知函数 的定义域为R, ,且当x﹤3 时, ,则下列结论中一定正确的是( )
A. B. C. D.
本题实质上与斐波那契数列有相似之处,但并非完全一致,因此不同水平的考生会采用不同的方法,导致解题花费的时间也不同。在单选题的压轴题备考中,多采用一题多变的教学模式——提思维、减负担、培探索、增信心、提效率,以适应各层次学生提高关键能力。
2.体现数学之美:巧妙地将数学知识与优美曲线相结合
第11题深刻地体现了高考数学中不等式在解决实际问题中的实用价值,它通过精确的数量关系描述与分析,帮助我们更加深入地理解和解决现实世界中的复杂问题,从而彰显了数学的严谨性和实用性。因此,教师应当从过去单纯教授技巧和练习题型的教学模式转向培养学生的思维能力,教授他们如何独立思考,如何运用所学知识解决实际问题。
3.强化对方法的深入理解和综合应用
第14题:甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两个各自从自己持有的卡片中随机选一张,并比较所选卡片上的数字大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用),则四轮比赛后,甲的总得分不小于2的概率为 .
2025届高考复习中,教师不仅要频繁检验学生对知识点的掌握程度,更应注重培养学生对解题方法的深入理解和综合应用能力。以这题用枚举法为例,这种方法在高考数学中展现出了其独特的优势,包括准确性高、全面性强、易于理解和操作、适用性强,等等。同时,教师教导学生在应用枚举法时,需要根据问题的具体情况进行权衡和选择,以确保解题的高效性和准确性。通过这样的教学方式,教师可以帮助学生更好地掌握数学知识,提升他们的解题能力和思维水平。
4.打破以往的命题模式,灵活、科学地确定试题的内容和顺序
第16题:已知 A(0, 3)和 P(3, )为椭圆 (a﹥b﹥0)上两点.(1)求 C 的离心率;(2)若过 P 的直线 l 交 C 于另一点 B,且△ABP 的面积为9,求 l 的方程.
2025届高三学生需要特别注意,今年解析几何试题安排在解答题的第2题,可见新课标卷已经打破了传统的命题模式,采取更加灵活和科学的方式来确定试题的内容和顺序。这种机动的试题顺序调整旨在打破学生机械式应试的惯性思维,同时也打破了教学中可能存在的僵化、刻板的训练模式,从而有效地防止了猜题、押题的情况发生。通过这样的调整,新课标卷能够更好地测试学生的应变能力和解决各种难度问题的能力。这一改革旨在引导教学,帮助学生全面掌握主干知识,提升基本能力,并培养他们灵活地整合知识、解决问题的能力。因此,2025届高三学生应适应这种变化,注重知识的全面性和应用的灵活性,为应对新挑战做好充分准备。
2025届高三学生在复习解析几何时,应特别关注一题多解的教学模式。通过一题多解的训练,不仅能加深对知识点的理解,还能在解题过程中锻炼思维能力和运算能力。这种教学模式有助于学生从多个角度思考问题,形成更加灵活的思维习惯。例如第16题,通过对比不同的解题方法,会发现用参数方程设点写出面积坐标公式可以更好地理解题目本质,利用平行四边形的性质及椭圆的对称性,提高解题速度,提升解决问题的综合能力。
5.强调推理能力、空间想象能力的考查
第17题:如图,四棱锥 P-ABCD 中,PA⊥底面 ABCD,PA=AC=2,BC=1,AB= .(1)若AD⊥PB,证明:AD∥平面PBC;(2)若AD⊥DC,且二面角 A-CP-D 的正弦值为 ,求 AD.
在考场上,不少学生被这道立体几何题困住。这道题目允许使用综合法或坐标法解答,虽然解题途径多样,但要在10分钟内完成却对许多学生来说颇具挑战。因此,2025届高三学生在复习立体几何部分时,建议深入研究真题,掌握解题的最佳策略,并要特别重视限时训练。通过设定时间限制来完成往年真题,可以有效锻炼解题速度和准确性,为高考做好充分准备。
6.强化综合性考查,考查知识之间的内在联系
第18题:已知函数 .(1)若 b = 0,且
≥0,求 a 的最小值;(2)证明:曲线 y = 是中心对称图形;(3)若 ﹥-2,当且仅当1﹤x﹤2,求 b 的取值范围.
本题在函数、导数试题中巧妙地融入了曲线的对称性这一几何性质,并深入地考查了学生求参数取值范围的能力。往后的复习中,教师应着重引导学生深入理解并掌握学科理论的本质属性和之间的关联。通过深化基础知识、基本原理和方法的教学,帮助学生构建完整的知识体系和网络结构。在导数复习方面,要特别注意求参数范围、分类讨论、零点以及不等式证明的训练。同时,加强分离参数、分类讨论、反证法等方法的实践,并让学生掌握证明题的解题技巧,例如本题中的第二问就是很好的实践案例。
重视理性思维,发挥了选拔功能
新课标I卷在难度设置上层次分明,不仅展示了思维的灵活性与深度,更在方法的选择上体现了综合、探究与创新的理念,科学、合理地划分了试题的区分度,充分彰显了高考数学在选拔人才方面的独特功能。
第19题:设 m 为正整数,数列 a1,a2,…,a4m+2 是公差不为0的等差数列,若从中删去两项 ai 和 aj(i ﹥ j)后剩余的4m 项可被平均分为 m组,且每组的4个数都能构成等差数列,则称数列 a1,a2,…,a4m+2 是(i, j)-的可分数列.(1)写出所有的(i, j),1≤i<j≤6,使得数列 a1,a2,…,a6 是(i, j)-可分数列;(2)当 m≥3 时,证明:数列 a1,a2,…,a4m+2 是(2,13)-可分数列;(3)从1,2,…,4m+2中一次任取两个数 i 和 j(i ﹤ j),记数列 a1,a2,…,a4m+2 是(i, j)-可分数列的概率为 Pm,证明:Pm﹥ .
本题以等差数列为背景,创新设问方式,通过引入数学新定义,为学生搭建了一个广阔的思维平台,旨在引导学生积极思考,在解题过程中领悟数学方法,并自主选择路径和策略来分析、解决问题。预计明年的新课标I卷第19题将继续延续这一趋势,对考生的综合素质和临场应变能力提出更高要求。这包括但不限于对信息的提取与加工能力、对数学符号的深入理解和准确推导能力、从具体到抽象和从一般到特殊的科学探究能力。这种设计不仅考查了学生的思维能力,更要求学生具备解决复杂问题的综合素养和关键能力,因此具有一定的难度。这样的题目设计有利于高校选拔出具备扎实数学基础和优秀思维能力的人才,同时也有利于中学数学教学更加注重培养学生的核心素养,提高学生的综合素质和解决问题的能力。
总之,在接下来的备考中务必全面把握核心知识点,强化基本能力,稳固基础,频繁回顾课本内容,始终以课程标准为导向。同时,我们要深入研究历年高考真题,紧密围绕高考评价体系展开学习,这样才能确保学习的主动性和高效性。面对多变的考试环境,我们应保持不变的应对策略,以稳健的步伐和自信的心态迎接挑战,从容不迫地应对考试。

